（pytorch）LSTM自编码器在西储数据的异常检测

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

旋转机械在现代设备中应用广泛，滚动轴承作为基础部件，是故障诊断的重点研究对象。本文研究了神经网络在轴承故障诊断方面的应用现状，并结合现有技术手段，通过建立自编码器模型，对西储大学轴承数据库中的数据实现了故障类型的分类，该方法直接作用在时域振动信号上，识别准确率高。

---

一、自编码器是什么？

引用一段莫烦的解释：
原来有时神经网络要接受大量的输入信息, 比如输入信息是高清图片时, 输入信息量可能达到上千万, 让神经网络直接从上千万个信息源中学习是一件很吃力的工作。
所以, 何不压缩一下, 提取出原图片中的最具代表性的信息, 缩减输入信息量, 再把缩减过后的信息放进神经网络学习.。这样学习起来就简单轻松了. 所以, 自编码就能在这时发挥作用. 通过将原数据白色的X 压缩, 解压 成黑色的X, 然后通过对比黑白 X ,求出预测误差, 进行反向传递, 逐步提升自编码的准确性.。训练好的自编码中间这一部分就是能总结原数据的精髓.。可以看出, 从头到尾, 我们只用到了输入数据 X, 并没有用到 X 对应的数据标签, 所以也可以说自编码是一种非监督学习。

总之，这是一种非监督学习，也就是不需要标签的学习方式，在工程领域，我们获得的数据往往是类不平衡的，正常的数据远远多于异常数据。这是显而易见的，毕竟机器正常运行才是常态，你总不能指望机器经常发生故障，或者动不动以高成本故意弄坏机器去取得异常数据。
言归正传，在解决这种类不平衡问题时，往往采取两种想法：
1、基于重构的思想，也就是我们今天做的自编码器。以自编码器为代表，我们使用类不平衡数据对自编码器模型进行训练，由于正常数据更多，模型训练后，对于正常数据，能够更好地还原出原数据，也就是误差会更小。反之，如果使用自编码器重构出来的输出跟原始输入的误差超出一定阈值（threshold）的话，则说明输入的是异常数据。
2、基于生成的思想，以GAN为代表，不赘述了。

二、代码实现环节

1.引入库

代码如下：

import torch
import copy
import torch.nn as nn
from torch.utils.data import DataLoader, Dataset
from sklearn.preprocessing import maxabs_scale
import scipy.io as sio
import numpy as np
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import pandas as pd
import random
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
from sklearn.metrics import precision_recall_curve

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

RANDOM_SEED = 42
np.random.seed(RANDOM_SEED)
torch.manual_seed(RANDOM_SEED)

# torch.manual_seed(1)    # reproducible

2.超参数

代码如下：

EPOCH = 150
LR = 0.005
DATA_NUM = 600
DATA_LEN = 400

3.导入数据

代码如下：

def data_preprocess(x):
    x = torch.Tensor(x)
    # x = maxabs_scale(x)
    return x


def prepare_data(path1, num, length):
    NC = r"D:\dataset\casedata_12khz\normal\97.mat"
    IF = r"D:\dataset\casedata_12khz\inner\105.mat"
    OF = r"D:\dataset\casedata_12khz\outer\130.mat"
    BF = r"D:\dataset\casedata_12khz\ball\118.mat"
    data = np.zeros([num, length], dtype=np.float32)  # [600,400]
    data = load_mat_data(path1, item_name="DE_time", num_points=num * length).reshape([num, length])
    data = torch.Tensor(data)  # (600, 400)
    return data  # data[num,len](600, 400)


def load_mat_data(path, item_name='DE_time', num_points=DATA_LEN * DATA_NUM):
    # get data from .mat file
    mat_data = sio.loadmat(path)  # a dictionary
    name_new = []
    # print(list(mat_data.keys()))
    # exit()
    for n in list(mat_data.keys()):
        if item_name in n:
            name_new.append(n)  # ['X097_DE_time']

    data = mat_data[name_new[0]]  # name_new[0] ==> 'X097_DE_time'
    # data = mat_data['X097_DE_time']  # [243938, 1]
    return data[:num_points]  # (240000, 1)


DATA_NORMAL = prepare_data(r"D:\dataset\casedata_12khz\normal\97.mat", num=DATA_NUM, length=DATA_LEN)
DATA_NORMAL = data_preprocess(DATA_NORMAL)  # (600, 400)
DATA_ANO_BALL = prepare_data(r"D:\dataset\casedata_12khz\ball\118.mat", num=300, length=DATA_LEN)
DATA_ANO_BALL = data_preprocess(DATA_ANO_BALL)  # (300, 400)
DATA_ANO_INNER = prepare_data(r"D:\dataset\casedata_12khz\inner\105.mat", num=300, length=DATA_LEN)
DATA_ANO_INNER = data_preprocess(DATA_ANO_INNER)  # (300, 400)
DATA_ANO_OUTER = prepare_data(r"D:\dataset\casedata_12khz\outer\130.mat", num=300, length=DATA_LEN)
DATA_ANO_OUTER = data_preprocess(DATA_ANO_OUTER)  # (300, 400)
DATA_ANOMALY = torch.cat((DATA_ANO_BALL,DATA_ANO_INNER,DATA_ANO_OUTER),dim=0)  # (900, 400)


# 数据预处理
train_DN, val_DN = train_test_split(
    DATA_NORMAL,
    test_size=0.15,
    random_state=RANDOM_SEED)

val_DN, test_DN = train_test_split(
    val_DN,
    test_size=0.33,
    random_state=RANDOM_SEED)

我们选取的西储轴承数据集数据是在驱动端的一个加速度值的时间序列（DE - drive end accelerometer data），以正常数据为例，我们选取的是载荷为0，转速在1797rpm（30r/s）下测量的数据，采样频率为12khz，所以每转采样约为400，我们选单个样本长度为400，由于在该条件下测得的正常数据点为243938个，所以我们将其分为600个样本，也就是600转。

代码解读：
1、data_preprocess(x)是将数据转换为tensor形式，这是由于pytorch在训练模型时需要tensor形式的数据。
2、prepare_data(path1, num, length)是将数据导入并转换为需要的shape【600，400】。
3、load_mat_data（）读取.mat格式文件的数据。
4、DATA_NORMAL ：正常数据，
DATA_ANO_BALL ：滚动体异常数据，
DATA_ANO_INNER：内圈异常数据，
DATA_ANO_OUTER ：外圈异常数据，
DATA_ANOMALY：上述三种异常数据集合。
由于数据长度限制，三种异常数据样本长度均为300，数据shape也就是【300, 400】
5、我们使用正常数据train_DN对自编码器模型进行训练，将DATA_NORMAL分为train_DN, val_DN，test_DN,分别具有510, 60，30个样本。

4.搭建网络

当训练一个自动编码器时，模型目标是尽可能地重构输入。这里的目标是通过最小化损失函数来实现的（就像在监督学习中一样）。这里所使用的损失函数被称为重构损失。常用的重构损失是交叉熵损失Cross Entropy Loss和均方误差MSE Loss。

接下来将以GitHub中的 LSTM Autoencoder为基础，并进行一些小调整。因为模型的工作是重建时间序列数据，因此该模型需要从编码器开始定义。

代码如下：

class Encoder(nn.Module):

    def __init__(self, seq_len, n_features, embedding_dim):
        super(Encoder, self).__init__()

        self.seq_len, self.n_features = seq_len, n_features
        self.embedding_dim, self.hidden_dim = embedding_dim, 2 * embedding_dim
        # 使用双层LSTM
        self.rnn1 = nn.LSTM(
            input_size=n_features,
            hidden_size=self.hidden_dim,
            num_layers=1,
            batch_first=True)

        self.rnn2 = nn.LSTM(
            input_size=self.hidden_dim,
            hidden_size=embedding_dim,
            num_layers=1,
            batch_first=True)

    def forward(self, x):
        x = x.reshape((1, self.seq_len, self.n_features))
        x, (_, _) = self.rnn1(x)
        x, (hidden_n, _) = self.rnn2(x)
        return hidden_n.reshape((self.n_features, self.embedding_dim))

编码器使用两个LSTM层压缩时间序列数据输入。
lstm1如下：

输入Hin	输出Hout
1	128

将输入的1维特征（本文中是加速度特征）升到128维，再由lstm2降维到64

输入Hin	输出Hout
128	64

值得注意的是我们取的是Encoder lstm网络的h_n而不是输出output作为输入到Decoder中。h_n：最后一个时间步的输出，即 h_n = output[:, -1, :]，虽然 lstm每个时刻 t 都会有输出，但是最后时刻的输出实际上已经包含了之前所有时刻的信息，所以一般我们只保留最后一个时刻的输出就够了。

接下来，我们将使用Decoder对压缩表示进行解码：

class Decoder(nn.Module):

    def __init__(self, seq_len, input_dim=64, n_features=1):
        super(Decoder, self).__init__()

        self.seq_len, self.input_dim = seq_len, input_dim
        self.hidden_dim, self.n_features = 2 * input_dim, n_features

        self.rnn1 = nn.LSTM(
            input_size=input_dim,
            hidden_size=input_dim,
            num_layers=1,
            batch_first=True)

        self.rnn2 = nn.LSTM(
            input_size=input_dim,
            hidden_size=self.hidden_dim,
            num_layers=1,
            batch_first=True)
        self.output_layer = nn.Linear(self.hidden_dim, n_features)

    def forward(self, x):
        x = x.repeat(self.seq_len, self.n_features)
        x = x.reshape((self.n_features, self.seq_len, self.input_dim))
        x, (hidden_n, cell_n) = self.rnn1(x)
        x, (hidden_n, cell_n) = self.rnn2(x)
        x = x.reshape((self.seq_len, self.hidden_dim))

        return self.output_layer(x)

解码器使用两个LSTM层，和一个Linear线性层
lstm3如下：

输入Hin	输出Hout
64	64

lstm4：

输入Hin	输出Hout
64	128

Linear：

输入Hin	输出Hout
128	1

这里将所有内容包装成一个易于使用的模块

class RecurrentAutoencoder(nn.Module):

    def __init__(self, seq_len, n_features, embedding_dim=64):
        super(RecurrentAutoencoder, self).__init__()
        self.encoder = Encoder(seq_len, n_features, embedding_dim).to(device)
        self.decoder = Decoder(seq_len, embedding_dim, n_features).to(device)

    def forward(self, x):
        x = self.encoder(x)
        x = self.decoder(x)
        return x

5.训练模型

编写一个辅助函数train_model，方便训练
代码如下：

model = RecurrentAutoencoder(seq_len=400, n_features=1, embedding_dim=64)
model = model.to(device)


# 训练模型
def train_model(model, train_dataset, val_dataset, n_epochs):
    optimizer = torch.optim.Adam(model.parameters(), lr=LR)
    criterion = nn.L1Loss(reduction='sum').to(device)
    # loss_func = nn.MSELoss()
    history = dict(train=[], val=[])
    best_model_wts = copy.deepcopy(model.state_dict())  # 复制模型的参数
    best_loss = 10000.0

    for epoch in range(1, n_epochs + 1):
        model = model.train()
        train_losses = []
        for seq_true in train_dataset:
            optimizer.zero_grad()
            seq_true = seq_true.cuda()
            seq_pred = model(seq_true)

            loss = criterion(seq_pred, seq_true.unsqueeze(1))  # !
            loss.backward()
            optimizer.step()

            train_losses.append(loss.item())

        val_losses = []
        model = model.eval()
        with torch.no_grad():
            for seq_true in val_dataset:
                seq_true = seq_true.to(device)
                seq_pred = model(seq_true)

                loss = criterion(seq_pred, seq_true.unsqueeze(1))
                val_losses.append(loss.item())

        train_loss = np.mean(train_losses)
        val_loss = np.mean(val_losses)

        history['train'].append(train_loss)
        history['val'].append(val_loss)

        if val_loss < best_loss:
            best_loss = val_loss
            best_model_wts = copy.deepcopy(model.state_dict())
        print(f'Epoch {epoch}: train loss {train_loss} val loss {val_loss}')

    model.load_state_dict(best_model_wts)
    return model.eval(), history

在每个epoch中，训练过程为模型提供所有训练样本，并评估验证集上的模型效果。注意，这里使用的批处理大小为1 ，即模型一次只能得到一个样本。另外还记录了过程中的训练和验证集损失。

值得注意的是，重构时做的是最小化L1损失，它测量的是 MAE（平均绝对误差），似乎比 MSE（均方误差）更好。

最后，我们将获得具有最小验证误差的模型，并使用该模型进行接下来的异常检测。现在开始做一些训练。

开始训练：

# 这一步耗时较长
model, history = train_model(
    model,
    train_DN,
    val_DN,
    n_epochs = EPOCH
)

6.绘制模型损失loss曲线

代码如下：

ax = plt.figure().gca()
ax.plot(history['train'])
ax.plot(history['val'])
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['train', 'test'])
plt.title('Loss over training epochs')
plt.show()

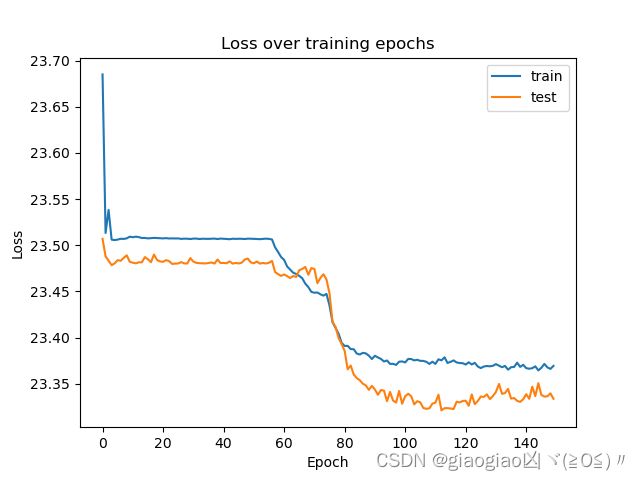
从可视化结果看出，我们所训练的模型基本收敛。看起来我们可能需要一个更大的验证集来优化模型，但数据有限，本文就不做展开了。

7.设定阈值

训练好了模型记得保存

MODEL_PATH = 'modelLSTM.pth'
torch.save(model, MODEL_PATH)

model = torch.load('modelLSTM.pth')
model = model.to(device)

后两行代码是调用已经存好的模型。

有了训练好了的模型，可以看看训练集上的重构误差。同样编写一个辅助函数来使用模型预测结果。
代码如下：

def predict(model, dataset):
    predictions, losses = [], []
    criterion = nn.L1Loss(reduction='sum').to(device)
    with torch.no_grad():
        model = model.eval()
        for seq_true in dataset:
            seq_true = seq_true.to(device)
            seq_pred = model(seq_true)

            loss = criterion(seq_pred, seq_true.unsqueeze(1))

            predictions.append(seq_pred.cpu().numpy().flatten())
            losses.append(loss.item())
    return predictions, losses

使用该辅助函数并配合频率直方图看一下各个数据的重构误差：

_, losses0 = predict(model, train_DN)
predictions1, losses1 = predict(model, test_DN)
predictions2, losses2 = predict(model, DATA_ANO_INNER)
predictions3, losses3 = predict(model, DATA_ANO_OUTER)
predictions4, losses4 = predict(model, DATA_ANO_BALL)

用直方图看一下误差是否符合正态分布：

# loss直方图，画图

plt.figure(figsize=(18, 8))
plt.subplot(1, 5, 1)
plt.hist(losses0, bins=50)
plt.xlabel("Loss")
plt.ylabel("Frequency")
plt.title("TRAINDATA")


plt.subplot(1, 5, 2)
plt.hist(losses1, bins=50)
plt.xlabel("Loss")
plt.ylabel("Frequency")
plt.title("TESTDATA")

plt.subplot(1, 5, 3)
plt.hist(losses2, bins=50)
plt.xlabel("Loss")
plt.ylabel("Frequency")
plt.title("INNER")

plt.subplot(1, 5, 4)
plt.hist(losses3, bins=50)
plt.xlabel("Loss")
plt.ylabel("Frequency")
plt.title("OUTER")

plt.subplot(1, 5, 5)
plt.hist(losses4, bins=50)
plt.xlabel("Loss")
plt.ylabel("Frequency")
plt.title("BALL")

plt.tight_layout(pad=1.08)
plt.show()

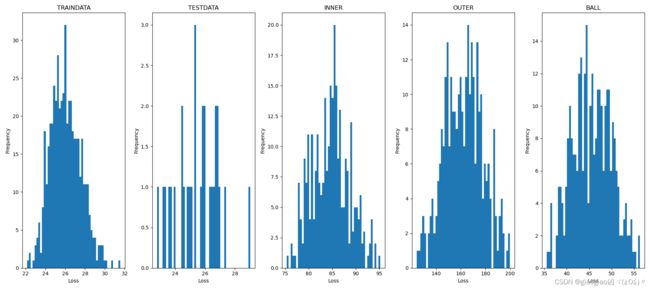
可以看出，正常数据和异常数据的重构误差区分度还是很高的，正常大约在22-32之间，异常则大于35，最接近正常的是滚动体故障，值得注意。这基本达到了我们做本次实验的目的，也就是通过自编码器的重构误差区分正常数据和异常数据，从而进行异常检测。
我们通过训练数据train_DN来找阈值，通过该阈值进行正异区分，这里我们采用箱型图的方法（也可以用置信区间的思想）

# 箱型图
df = pd.DataFrame(losses0)
print(df.describe())
df.plot.box(title="Box Chart")
plt.grid(linestyle="--", alpha=0.3)
plt.show()

结果如下：

# count  510.000000
# mean    26.040200
# std      1.524841
# min     22.158352
# 25%     24.937375
# 50%     25.945716
# 75%     27.064570
# max     31.567074

可以看出训练数据有两个样本偏移了主体数据，舍弃，最后由箱型图得到的阈值为max=31.567074

THRESHOLD = 31.567074
# 取阈值threshold为31.567074

8.评价指标

在类不平衡问题中评价指标只有accuracy是远远不够的，这里正常数据我们取test_DN的30个样本，train_DN和val_DN都参与了模型训练，不可以在评价时采用。由于类不平衡问题一般异常数据远低于正常，而正常数据只有30个样本，这里我们也从900个异常样本中随机取30个异常数据。
下面是对样本进行打标签，y_pred代表模型预测出的样本正异结果，y_true则是实际样本的正异，1代表正，0代表异。
评价指标如下：

1.准确率 （accuracy)
准确率表示被正确分类的样本占总样本的比例

2.召回率（recall）、灵敏度（sensitive）、真正率（true positive rate）
召回率是覆盖率的度量，表示有多少正例被正确分类

3.精确率、精度（Precision）
精度表示被分为正例的示例中实际为正例的比例

4.综合评价指标F-Measure
精度P和召回率R有时候会出现的矛盾的情况，这样就需要综合考虑他们，最常见的方法就是F-Measure（又称为F-Score）。 F-Measure是Precision和Recall加权调和平均

5.ROC曲线
通常分类的阈值越低（把得分更低的样例判定为正例），则模型对正例识别能力越强，真正率（true positive rate）也越高，但同时对负例的误判率也会越高，假正率（false positive rate）也越高。
ROC曲线形象化表示这一变化。

y_pred =[]
for l in losses1:
    if l <= THRESHOLD:y_pred.append(1)
    elif l > THRESHOLD:y_pred.append(0)
for l in losses5:
    if l <= THRESHOLD:y_pred.append(1)
    elif l > THRESHOLD:y_pred.append(0)
# print(y_pred)

y_true = torch.tile(torch.Tensor([[1],[0]]),(1,30)).reshape(-1)
# print(y_true)

target_names = ['class0','class1']
print(classification_report(y_true,y_pred,target_names = target_names))

---

结果：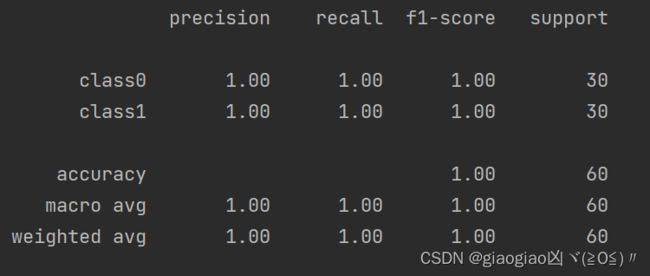
如图所示，准确率accuracy为1.0，其他二元分类评价指标precision，recall等都为1.0，代表至少在这些样本中，模型分类能力很强。

ROC、AUC、KS值:

from sklearn.metrics import roc_curve, auc
fpr,tpr,threshold = roc_curve(y_true, y_pred) #y_score是预测概率，y_test是真实值类别
roc_auc = auc(fpr,tpr) ###计算auc的值
print(roc_auc)  # 1.0
ks=max(tpr-fpr)
print(ks)  # 1.0
plt.figure()
lw = 2
plt.figure(figsize=(10,10))
plt.plot(fpr, tpr,
         lw=lw, label='ROC curve (area = %0.2f)' % roc_auc) ###假正率为横坐标，真正率为纵坐标做曲线
plt.plot([0, 1], [0, 1], lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC')
plt.legend(loc="best")
plt.show()

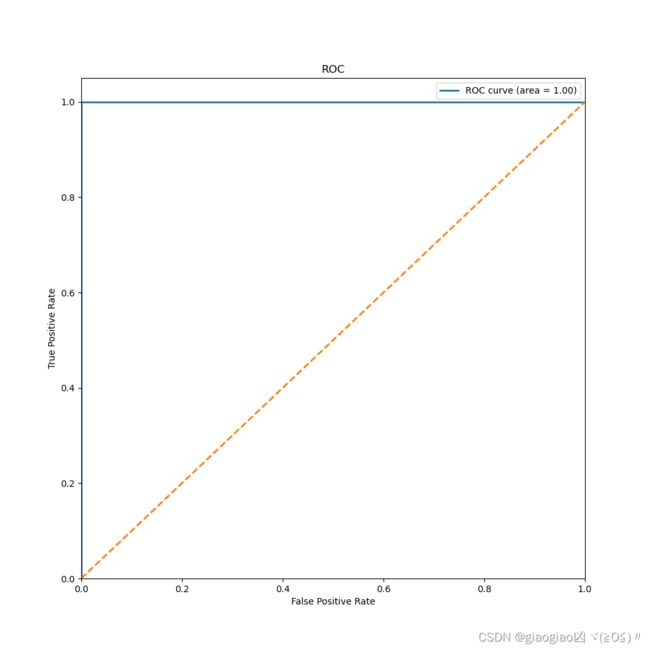
AUC值是ROC曲线下方的面积，越接近于1，模型效果越好，本文为1.0
KS值用来评估模型的区分能力，KS值越大，模型的区分能力越强，本文为1.0

三、总结

到目前为止，该实战案例已经告一段落了。在本案例中，我们一起学习了如何使用 PyTorch 创建 LSTM 自动编码器并使用它来检测西储轴承数据集的加速度信号异常。结果还是不错的，基本达到了最初的设想，接下来可以有以下改进：1、将该模型放到其他载荷下的数据中测试其泛化能力。2、改用其他模型针对西储数据进行异常检测，本文采用的lstm自编码器对于西储数据可能效果不是很好，长短时记忆网络lstm都可用于对序列数据的处理，如果序列数据的整体顺序很重要，如随着时间，轴承故障程度加深，那用长短时记忆网络处理效果很好；如果整体顺序没有意义，那意义不大。凯斯西储大学公开数据集中的数据仅记录了轴承故障信息，轴承损伤压根就是人为钻出来的，数据之间的整体顺序并不重要，所以可能不宜采用lstm，本文只是用其作为简单尝试。
还有最后要感谢师兄的指导！@燕策西

四、参考材料

西储轴承数据网站，大家可以在该处下载本文数据
基于简单CNN的西楚数据集智能诊断。师兄写的文章！本文就是在此基础上一步步做的
【深度学习】在PyTorch中使用 LSTM 自动编码器进行时间序列异常检测
二元分类指标参照该文章
箱型图参照该文章
莫烦自编码器