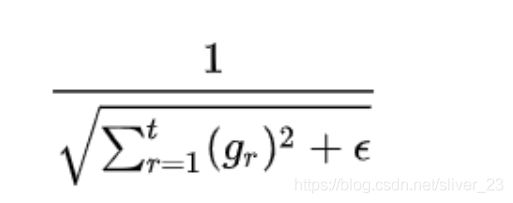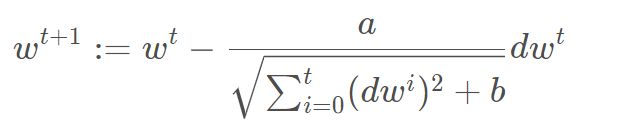李宏毅机器学习2020-作业1：预测PM2.5的值（li‘near regression）

一. 问题描述

数据下载网盘链接：https://pan.baidu.com/s/1X_E11htmPWiDIF6UAVyJQw 
提取码：i94n 

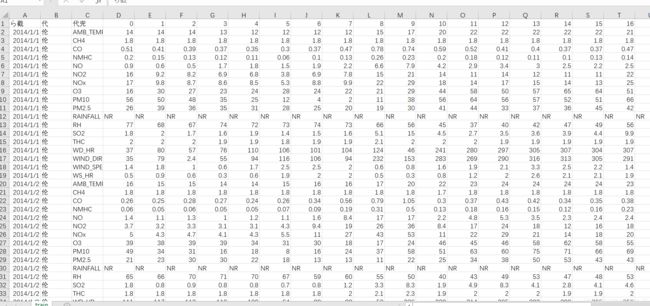
先打开train.csv，显示如下:

 有乱码，不管他就行。

可以看到train.csv是一个（18（检测类型）x 20（天数）x  12（月份））x 24（小时）的矩阵

即4320x24的矩阵 

二. 数据预处理

先进行必要的数据包的导入。

import sys    #该模块提供对解释器使用或维护的一些变量的访问，以及与解释器强烈交互的函数
import math   #数学运算的库
import numpy as np     #Python的一个扩展程序库，支持大量的维度数组与矩阵运算
import pandas as pd    #一个强大的分析结构化数据的工具集

然后我们可以开始进行数据的预处理啦！

导入数据，注意路径中要用" / "

data = pd.read_csv("D:/Work1/train.csv", encoding='big5') #big5是繁体字的编码方式。

通过查看train我们可以看到，数据的前三列是不需要处理的注释，所以把它消去。

同时有一个参数rainfall，NR表示没有下雨，因此我们把其全用0替换。

data = data.iloc[:, 3:]
data[data == 'NR'] = 0
data = data.to_numpy()  # 将数据保存再矩阵中
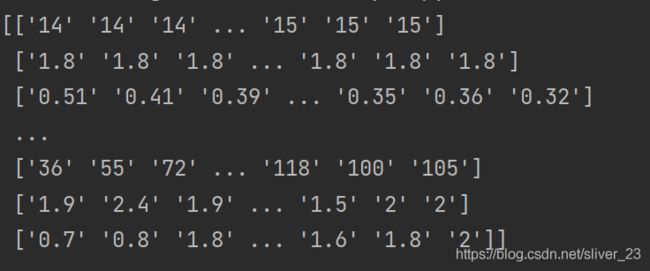
print(data)

运行，打印出来如下：

 接下来的分析采用滑动窗口的思想，将4320*24的矩阵拼成一个18*（480*12）的矩阵。

# 对数据进行重组，将原始的18×20×12×24的数据按照每月重组成12×18×480的数据
month_data = {}
for month in range(12):
    sample = np.empty([18,480], dtype=float)
    for day in range(20):
        sample[:, day * 24: (day + 1) * 24] = raw_data[18 * (20 * month + day): 18 * (20 * month + day + 1), :]
    month_data[month] = sample

构建x，y训练集，

每九个小时的训练样本来预测第十个小时的PM2.5,因此用x来存放数据内所有可能的连续9个小时的数据合集，y来存放对应的第10个小时的数据集（将每9个小时的数据放在同一行）

因为1个月20天都是连续的，所以可以将20天的480个小时看成连续的，所以一个月就有480-9=471个data，一年有471×12=5652个data，同样有5652个 Label（第10个小时的PM2.5），采用这种方法可以构建较多的data。(每个data中有9×18个数据)

x = np.empty([12 * (480 - 9), 18 * 9],dtype=float)
y = np.empty([12 * (480 - 9), 1],dtype = float)
for month in range(12):
    for i in range(471):
        x[month * 471 + i, :] = month_data[month][:, i:i+9].reshape(1,-1) #.reshape()可以使数据变为一行。因为x[][]是一行= =
        y[month * 471 + i, 0] = month_data[month][9, 9 + i] # PM2.5位于下标9的位置

print(x)
print(y)

看看打印出的效果

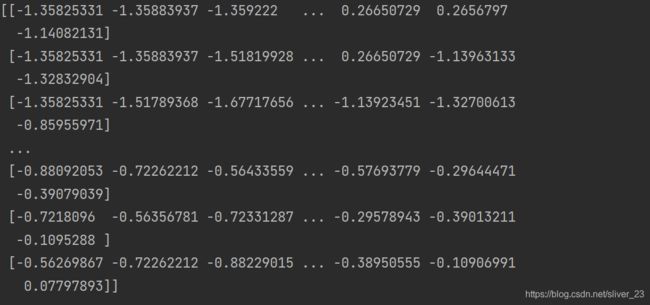
然后我们进行归一化（Normalization）

最常见的标准化方法是Z标准化，也是SPSS中最为常用的标准化方法，spss默认的标准化方法就是z-score标准化。
也叫标准差标准化，这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。

其转换函数为：x* = (x - μ ) / σ

x_mean = np.mean(x, axis=0) # axis=0计算每一列的标准差
x_std = np.std(x, axis=0)
for i in range(len(x)):
    for j in range(len(x[0])):
        if x_std[j] != 0:
            x[i][j] = (x[i][j] - x_mean[j]) / x_std[j]

print(x)

康康结果

随后将训练集以8：2的方式分成训练集和验证集，初步判断下我们模型的好坏

x_train = x[:math.floor(len(x) * 0.8), :]
y_train = y[:math.floor(len(x) * 0.8), :]
x_validation = x[math.floor(len(x) * 0.8):, :]
y_validation = y[math.floor(len(x) * 0.8):, :]
print(x_train)
print(y_train)
print(x_validation)
print(y_validation)

三. 开始训练

1.loss function采用均方根误差函数（Root Mean Square Error）

 

2. 根据上述函数计算出的gradient为：

 

 3. 自适应学习率adagard方法，每次学习率都等于其除以之前所有的梯度平方和再开根号，即下图所示的公式

 

4.参数更新公式

#开始求参数啦！
dim = 18 * 9 + 1  # 参数的维数
w = np.ones([dim, 1]) # 参数矩阵
x_train = np.concatenate((np.ones([len(x_train), 1]), x_train), axis=1).astype(float) #在x_train矩阵前面加上一列全1的数据
adagard = np.zeros([18*9+1, 1]) #采用adagard方法更新学习率
iter_times = 40000  #迭代次数
learning_rate = 100.0 #学习率，随便设置初始值就好
eps = 0.0000001 # 在adagard方法中，需要用梯度值的平方之和作为分母，为了防止分母为0，加上一个极小值
for i in range(iter_times):
    loss = np.sqrt(np.sum(np.power(np.dot(x_train, w) - y_train, 2) / len(x_train)))
    if i % 100 == 0:
        print("迭代次数为：" + str(i), "      ", "损失值为：" + str(loss))
    gradient = np.dot(x_train.transpose(), (np.dot(x_train, w) - y_train)) / (len(x_train) * loss)
    adagard += gradient ** 2
    w = w - learning_rate * gradient / np.sqrt(adagard + eps)

# 保存参数w
np.save('weight.npy', w)

可以看到随着迭代次数的增加，损失值在变小。（虽然还是很大，毕竟我们用的是线性模型） 

求出参数啦，此时用验证集来验证下。

无需数据预处理和归一化，直接套公式即可：

w = np.load("weight.npy")
x_validation = np.concatenate((np.ones([len(x_validation), 1]), x_validation), axis=1).astype(float)
for i in range(iter_times):
    loss = np.sqrt(np.sum(np.power(np.dot(x_validation, w) - y_validation, 2) / len(x_validation)))
    gradient = np.dot(x_validation.transpose(), (np.dot(x_validation, w) - y_validation)) / (len(x_validation) * loss)
    adagard += gradient ** 2
    w = w - learning_rate * gradient / (np.sqrt(adagard + eps))

print("迭代40000次以后的损失值为：" + str(loss))

四. 预测后10天的PM2.5的值

流程：数据预处理----》预测PM2.5的值----》保存到表格文件中

上代码！

# 数据预处理
testdata = pd.read_csv("D:/Work1/test.csv", header = None, encoding="big5")
testdata[testdata == 'NR'] = 0
testdata = testdata.iloc[:, 2:]
testdata = testdata.to_numpy()
test = np.empty([240,18 * 9],dtype=float) #创建一个240行18*9列的空数列用于保存textdata的输入
for i in range(240):
    test[i, :] = testdata[18 * i:18 * (i + 1), :].reshape(1, -1)

# 归一化
test_mean = np.mean(test, axis=0)
test_std = np.std(test, axis=0)
for i in range(len(test)):
    for j in range(len(test[0])):
        if test_std[j] != 0 :
            test[i][j] = (test[i][j] - test_mean[j])/ test_std[j]
test = np.concatenate((np.ones([len(test), 1]), test), axis=1).astype(float)

# 预测开始
w = np.load("weight.npy")
ans_y = np.dot(test,w)

with open("Prediction.csv",'w',newline='') as Prediction_file:
    csv_writer = csv.writer(Prediction_file)
    header = ["id", "values"]
    print(header)
    csv_writer.writerow(header)
    for i in range(240):
        row = ["id_"+ str(i),str(ans_y[i][0])]
        csv_writer.writerow(row)
        print(row)

运行后成果就出来啦！

到这里作业就结束了。作为一枚python和深度学习的小白，这两天从零开始，参考了很多资料总算把这个完成了，成就感MAX!