算法——对称加密——AES(Rijndael)
AES-Rijndael
- 简介
-
- 整体结构
-
- 算法特点:
- 密钥取值范围
- 整体图例
- 数据处理
- 加密过程
-
- SubBytes(字节代换)
- ShiftRows(行移位)
- MixColumns(列混淆)
- AddRoundKey(加轮密钥,密钥加法)
-
- 密钥扩展
- 加密过程
- 总结:
简介
因为 DES的诸多弊端。因此需要更高级的算法。所以AES(Advanced Encryption Standard,AES)孕育而生。
1.1998年8月12号。在首届AES会议上,指定了15个候选算法。
2.1999年3月22号。在第二次AES会议上,将算法缩减至5个。
3.2000年4月13号。在第三次AES会议上,将5个候选算法的各种分析算法进行了讨论。
4.2000年12月2号。NIST宣布最终获胜者为Rijndael。2001年11月出版了最终标准FIPS PUB197。
| 名称 | 提交者 |
|---|---|
| MARS | IBM |
| RC6 | RSA 公司 |
| Rijndael | Daemen,Rijmen |
| Serpent | Anderson,Biham,Knudsen |
| Twofish | Counterpane 公司 |
整体结构
算法特点:
1.不属于 Feistel 网络。
2.加密、解密相似但不对称。
3.支持128位数据加密。
4.支持128/196/256密钥长度。
5.有较好的数学理论作为基础。
6.结构简单,速度快。
密钥取值范围
不同的密钥的区别主要体现在密钥长度、分组长度和轮数的区分。不同密钥的主要区分如图1-1所示。

整体图例
数据处理
AES为分段加密,每次只能加密128 bit 数据,即16字节 byte 数据。
首先将需要加密的数据列成 4*4的字节矩阵。示例图如1-2 所示。

加密过程
加密过程共分为4部分:
1:SubBytes(字节代换)
2:ShiftRows(行移位)
3:MixColumns(列混淆)
4:AddRoundKey(加轮密钥,密钥加法)
下面将逐步进行详细讲解。
SubBytes(字节代换)
首先将每一个字节的值根据 s-box进行替换。替换规则如下所示。
替换规则如图2-1-1所示。
s-box如图2-1-2所示。
示例图如2-1-3所示。
s-box如下图 :
ShiftRows(行移位)
移动规则为
第一行不变
第二行循环左移1个字节
第三行循环左移2个字节
第四行循环左移3个字节
替换规则如图2-2-1所示。
示例图2-2-2所示。

MixColumns(列混淆)
加密方法:待加密矩阵左乘修补矩阵(常量矩阵)。
常量矩阵中有三种值,01、02、03。
1. 数据乘以1就是自身。
例如: 01× C9=C9
2. 数据乘以2可以直接认为左移一位。如果被乘的值大于或等于0x80,这时乘法的结果就是左移1比特位再用值0x1b异或。它防止了“域溢出”并保持乘法的乘积在范围以内。(即最左侧为1时, 需要和. 0x1b异或 )。
例如 02 × C9 = 02 × 11001001=10010010。 因为结果 大于 80(10000000)。 所以 10010010再与1B进行异或运算。 10010010 ⊕ 00011011 = 10001001。所以结果为89(10001001)。
3. 数据乘以3乘以3时。 0x03 分解为2的幂之和。所以 0x03 = 0x02 + 0x01。因此 03 × C9=(0x02 + 0x01) × C9。
整体计算示例图如2-3-1所示。
单列计算示例图如2-3-2、2-3-3所示。
AddRoundKey(加轮密钥,密钥加法)
此步骤为字节矩阵与密钥矩阵进行xor运算。得出结果。此轮的xor运算相对简单,重点难点为密钥扩展部分。
密钥扩展:以密钥为128位为例。如图1-1所示,由于AES为多轮加密,所以整体加密流程共需要一个初始转换和10轮密钥。
因此 128位的密钥 需要生成的 密钥总数为 128 bits + 128 bits * 10 = 1408 bits
所以密钥扩展算法需要将128位的密钥扩展为 1408位密钥。
密钥扩展
示例:假设AES的密钥为:2B7E151628AED2A6ABF7158809CF4F3C。
则
第0轮:
W0:“2B7E1516”,
W1:“28AED2A6”,
W2:“ABF71588”,
W3:“09CF4F3C”.
第1轮:
W4 = 逆(w0 ⊕Temp )= ‘a0fafe17’
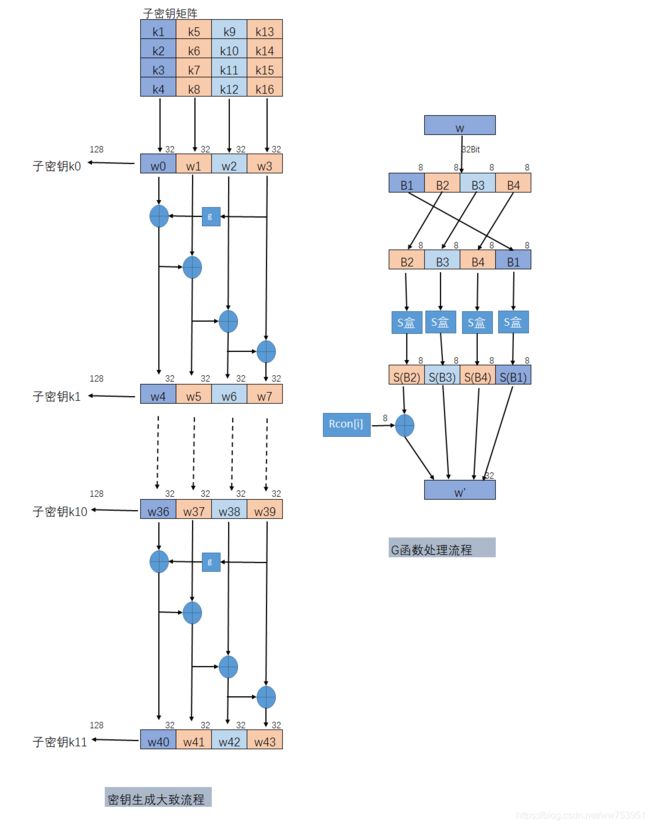
Temp=g(W3)。即g函数计算W3的结果。
其中g函数的过程为三步骤,如图2-4-1的右侧所示。
1:左移动 一位
2:S 盒 转换
3:与 该轮的RCon进行异或操作,其中Rcon轮系数为常量数组,常量的值如图 2-4-2所示。
所以:第1轮的详细计算步骤如下:
第一步: w3进行循环位移
Rotword1: ‘09CF4F3C’ -> ‘CF4F3C09’
第二步:对结果进行S盒加密:(如CF -> 8a, 4F -> 84)
Subword1: ‘CF4F3C09’ -> ‘8a84eb01’
第三步,S盒加密结果,与该轮的RCon进行异或操作。
Temp = 逆(Subword⊕RCon(1))= “8b84eb01”
第四步,将temp结果与上一轮的w[i-4]进行异或操作,因此,
W4 = 逆(w0 ⊕Temp )= ‘a0fafe17’
W5 = 逆(w1 ⊕ w4 ) = ‘88542cb1’
W6 = 逆(w2 ⊕ w5 ) = ‘23a33939’
W7 = 逆(w3 ⊕ w6 ) = ‘2a6c7605’
每一轮类似,但RCon每轮有指定的值,如此循环调用一共十次,加上第0轮的四个字,一共44个字。
代码运行结果w0-w44:
[“2B7E1516”,“28AED2A6”,“ABF71588”,“09CF4F3C”,
“A0FAFE17”,“88542CB1”,“23A33939”,“2A6C7605”,
“F2C295F2”,“7A96B943”,“5935807A”,“7359F67F”,
“3D80477D”,“4716FE3E”,“1E237E44”,“6D7A883B”,
“EF44A541”,“A8525B7F”,“B671253B”,“DB0BAD00”,
“D4D1C6F8”,“7C839D87”,“CAF2B8BC”,“11F915BC”,
“6D88A37A”,“110B3EFD”,“DBF98641”,“CA0093FD”,
“4E54F70E”,“5F5FC9F3”,“84A64FB2”,“4EA6DC4F”,
“EAD27321”,“B58DBAD2”,“312BF560”,“7F8D292F”
,“AC7766F3”,“19FADC21”,“28D12941”,“575C006E”,
“D014F9A8”,“C9EE2589”,“E13F0CC8”,“B6630CA6”]
加密过程
将待加密矩阵与密钥扩展后的结果进行xor运算。示例图如2-4-3所示。
因此AES重复以上加密步骤,共重复执行N轮,N取决于密钥长度。最后一轮没有 MixColumns 步骤。经过多轮后,数据加密完毕。
总结:
AES为现阶段使用较频繁的对称加密算法。算法为Rijindael。Rijindael算法要求在加密前用特定的密钥产生所有的子密钥,其支持的密钥有128位、192位、256位。一次加密的数据为固定长度。
------------------------------------------END-------------------------------------------