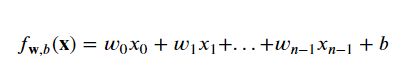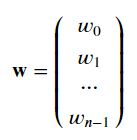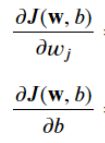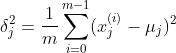吴恩达Couresa课程——第二部分：监督学习week2 （未完待续，见下一篇）

如有任何公式错误或者文字说明错误，请留言指正哦~~~~

问题引入

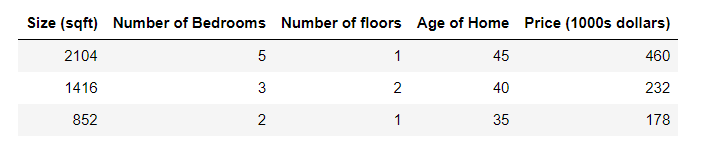
描述：下面您需根据以下数据构建一个线性回归模型，并预测一栋拥有1200平方英尺、3间卧室、1层楼、40年历史的房子。

一、多元线性回归模型

1.1 多元线性回归函数

以上表格内给出了4个特征（大小、卧室数量、地板数量、房子年龄）分别记为x1、x2、x3、x4，每个特征对应一个wi。多元特征线性回归函数一般形式为

写成向量形式为：

w和x之间是点乘。

我们的目标便是利用已知数据通过梯度下降算法找到最合适的w(这里是矢量形式)和b。

1.2 转换成矩阵

矩阵的每一行表示一个示例，列数表示特征数。当有m个示例n个特征时，｛X｝是一个具有维度（m行，n列）的矩阵。

因为每个特征对应一个w。所以有向量：

1.3 多元线性回归模型的代价函数

fw,b是预测值，y是实际值。

1.4 多元线性回归模型的梯度下降函数

化简偏导得到：

n是特征数量，m是样例个数。

收敛时的w（矢量形式）和b即为所求。

二、代码实现

2.1 代价函数

#代价函数
def compute_cost(X, y, w, b): 
    """
    compute cost
    Args:
      X (ndarray (m,n)): Data, m examples with n features
      y (ndarray (m,)) : target values
      w (ndarray (n,)) : model parameters  
      b (scalar)       : model parameter
      
    Returns:
      cost (scalar): cost
    """
    m = X.shape[0]  #样例个数
    print(f"m={m}")
    cost = 0.0
    for i in range(m):                                
        f_wb_i = np.dot(X[i], w) + b           #(n,)(n,) = scalar (see np.dot)
        cost = cost + (f_wb_i - y[i])**2       #scalar
    cost = cost / (2 * m)                      #scalar    
    return cost

2.2 计算梯度-偏导数

# 计算梯度
def compute_gradient(X, y, w, b):
    '''
    :param X: 矩阵，每一行代表一个示例向量
    :param y: 列表
    :param w: 向量
    :param b: 标量
    :return:
        sum_dw(标量，wj对于代价函数的偏导)
        sum_db(标量，b对于代价函数的偏导)
    '''
    m,n = X.shape
    sum_dw = np.zeros((n,))
    sum_db = 0
 
    for i in range(m):
        err = (np.dot(X[i],w) + b) - y[i]
        for j in range(n):
            sum_dw[j] = sum_dw[j] + err*X[i,j]
        sum_db = sum_db + err
    sum_dw = sum_dw/m
    sum_db = sum_db/m
 
    return sum_dw,sum_db

2.3 梯度迭代函数

def gradient_descent(X, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters): 
    """
    Performs batch gradient descent to learn theta. Updates theta by taking 
    num_iters gradient steps with learning rate alpha
    
    Args:
      X (ndarray (m,n))   : 矩阵，每一行代表一个示例向量
      y (ndarray (m,))    : 目标值
      w_in (ndarray (n,)) : w初始值，向量 
      b_in (scalar)       : b初始值，标量
      cost_function       : function to compute cost
      gradient_function   : function to compute the gradient
      alpha (float)       : Learning rate
      num_iters (int)     : number of iterations to run gradient descent
      
    Returns:
      w (ndarray (n,)) : 训练出的w和b
      b (scalar)       : Updated value of parameter 
      """ 
    # An array to store cost J and w's at each iteration primarily for graphing later
    #一个数组，用于存储每次迭代的成本J，主要用于以后的绘图
    J_history = []
    # copy.deepcopy()函数是一个深复制函数。所谓深复制，就是从输入变量完全复刻一个相同的变量，无论怎么改变新变量，原有变量的值都不会受到影响。
    w = copy.deepcopy(w_in)  #avoid modifying global w within function 避免在函数内修改全局w
    b = b_in
    
    for i in range(num_iters):

        # Calculate the gradient and update the parameters
        # 计算梯度并使用gradient_function更新参数
        dj_db,dj_dw = gradient_function(X, y, w, b)   

        # Update Parameters using w, b, alpha and gradient
        w = w - alpha * dj_dw               ##None
        b = b - alpha * dj_db               ##None
      
        # Save cost J at each iteration
        if i<100000:      # prevent resource exhaustion 
            J_history.append( cost_function(X, y, w, b))
        # Print cost every at intervals 10 times or as many iterations if < 10
        # 每隔10次打印一次成本，如果<10次，则重复次数相同
        # math.ceil：向上取整，四舍五入。
        if i% math.ceil(num_iters / 10) == 0:
            print(f"Iteration {i:4d}: Cost {J_history[-1]:8.2f}   ")
        
    return w, b, J_history #return final w,b and J history for graphing

2.4 设置学习率，并利用模型进行预测

注意：在预测前，要将数据集进行特征缩放。

什么是特征缩放？下个标题写一写~~~~

标准化：

def zscore_normalize_features(X):
    """
    computes  X, zcore normalized by column
    
    Args:
      X (ndarray): Shape (m,n) input data, m examples, n features
      
    Returns:
      X_norm (ndarray): Shape (m,n)  input normalized by column
      mu (ndarray):     Shape (n,)   mean of each feature
      sigma (ndarray):  Shape (n,)   standard deviation of each feature
    """
    # ,找到每列/特征的平均值
    mu     = np.mean(X, axis=0)                 # mu will have shape (n,)
    #找到每个列/特征的标准偏差
    sigma  = np.std(X, axis=0)                  # sigma will have shape (n,)
    # element-wise, subtract mu for that column from each example, divide by std for that column
    #元素方面，从每个示例中减去该列的mu，除以该列的std
    X_norm = (X - mu) / sigma      

    return (X_norm, mu, sigma)
 

下面先将进行特征缩放后的代码放进来：

if __name__ == '__main__':
    X_train = np.array([[2104, 5, 1, 45], [1416, 3, 2, 40], [852, 2, 1, 35]])
    Y_train = np.array([460, 232, 178])
    # 将X训练集拿去标准化
    X_train, mu, sigma = zscore_normalize_features(X_train)
    # print(X_train)
    # print(Y_train)
    # 设置学习率等
    w_init = np.array([0, 0, 0, 0])
    b_init = 0
    alpha = 0.5
    num_iters = 10000
    w_pre, b = gradient_descent(X_train, Y_train, w_init, b_init, alpha, num_iters)
    print(f"预测出的w:{w_pre}")
    print(f"预测出的b:{b}")
    # 预测
    X_forecast = [1200, 3, 1, 40]
    X_forecast = (X_forecast - mu) / sigma
    print(f"压缩后的测试数据{X_forecast}")
    X_predice_price = np.dot(X_forecast, w_pre) + b
    print(f"一个1200平米，3个卧室，1层楼，存在40年的房屋 = ${X_predice_price * 1000:0.0f}")

运行结果：

三、特征缩放

3.1 特征缩放作用

面对特征数量较多的时候，保证这些特征具有相近的尺度（无量纲化），可以使梯度下降法更快的收敛。

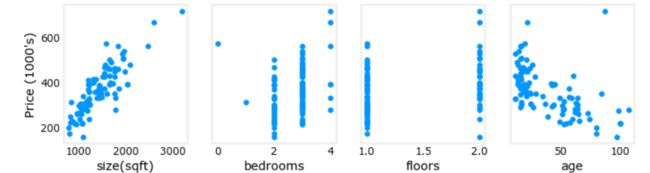
拿上面“问题引入”里得数据来说，各个特征的范围差距太大，我们将每个特征对价格的影响可视化，可以看出哪些因素对价格影响更大。会得到以下图像：

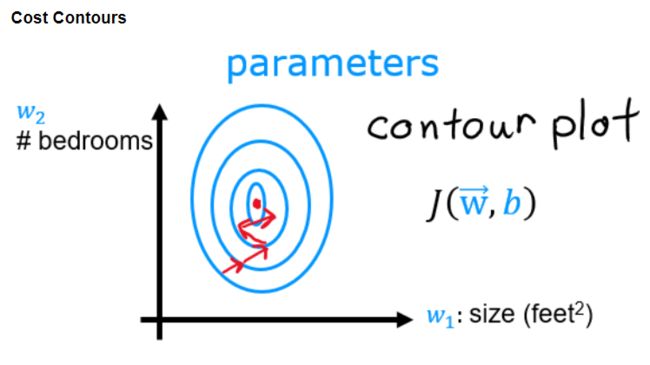
由于各个特征的数量差距过大，代价函数的等高线将会是扁长的，在梯度下降时也会是曲折的，而且计算时长相对会很长（因为学习率是通用的，为了照顾尺度大的特征，学习率必须设置的很小，学习率越小，下降速度就越慢）：

特征缩放将每个特征的范围统一，可以使梯度下降变”平滑“，并且大大提高计算速度（因为可以调大学习率））

3.2 特征缩放方法

1. 均值归一化

公式：

，其中，

为样本中该特征的均值。

# 均值归一化
def MeanNormalization(x):
   '''x为列表'''
    return [(float(i)-np.mean(x))/float(max(x)-min(x)) for i in x]

2、 Z-score标准化(推荐)

公式：

其中，

为

矩阵中的特征（或列),

为样本序号。

为特征j的均值，

为特征j的标准差。

 # Z-score标准化
def zscore_normalize_features(X):
    '''x是(m,n)的矩阵，m为样本个数，n为特征数目'''
    # 找每列(特征)均值
    mu = np.mean(X,axis=0)
    # 找每列(特征)标准差
    sigma = np.std(X,axis=0)
    X_norm = (X - mu) / sigma
 
    return (X_norm, mu, sigma)

四、特征工程和多项式回归

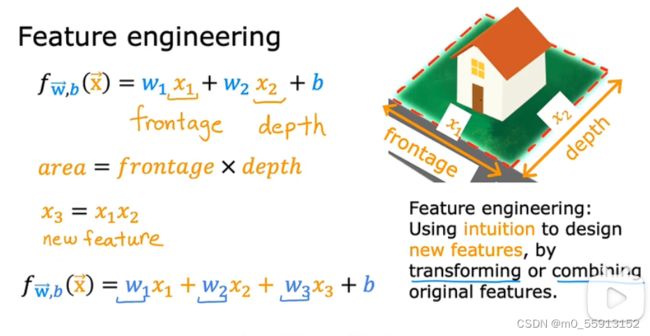
4.1 特征工程

通过直觉对原始特征进行转化或联合得到新的特征，来得到更好的模型。

如下图所示例子，将长和宽转化为房屋的面积。

4.2 多项式回归