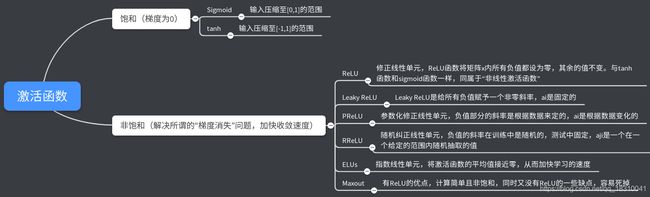
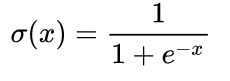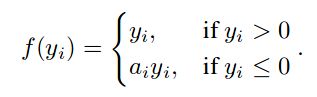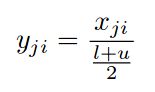激活函数的性质、表达式及其优劣：Sigmoid -> Tanh -> ReLU -> Leaky ReLU 、PReLU、RReLU 、ELUs-> Maxout
激活函数的性质
1. 非线性：即导数不是常数。保证多层网络不退化成单层线性网络。这也是激活函数的意义所在。
2. 可微性：可微性保证了在优化中梯度的可计算性。传统的激活函数如sigmoid等满足处处可微。对于分段线性函数比如ReLU，只满足几乎处处可微（即仅在有限个点处不可微）。对于SGD算法来说，由于几乎不可能收敛到梯度接近零的位置，有限的不可微点对于优化结果不会有很大影响。
3. 计算简单：正如题主所说，非线性函数有很多。激活函数在神经网络前向的计算次数与神经元的个数成正比，因此简单的非线性函数自然更适合用作激活函数。这也是ReLU之流比其它使用Exp等操作的激活函数更受欢迎的其中一个原因。
4. 非饱和性（saturation）：饱和指的是在某些区间梯度接近于零（即梯度消失），使得参数无法继续更新的问题。最经典的例子是Sigmoid，它的导数在x为比较大的正值和比较小的负值时都会接近于0。更极端的例子是阶跃函数，由于它在几乎所有位置的梯度都为0，因此处处饱和，无法作为激活函数。ReLU在x>0时导数恒为1，因此对于再大的正值也不会饱和。但同时对于x<0，其梯度恒为0，这时候它也会出现饱和的现象。Leaky ReLU[3]和PReLU的提出正是为了解决这一问题。
5. 单调性（monotonic）：即导数符号不变。当激活函数是单调的时候，单层网络能够保证是凸函数。
6. 输出范围有限：有限的输出范围使得网络对于一些比较大的输入也会比较稳定，这也是为什么早期的激活函数都以此类函数为主，如Sigmoid、Tanh。但这导致了前面提到的梯度消失问题，而且强行让每一层的输出限制到固定范围会限制其表达能力。因此现在这类函数仅用于某些需要特定输出范围的场合，比如概率输出（此时loss函数中的log操作能够抵消其梯度消失的影响）、LSTM里的gate函数。
7. 接近恒等变换（identity）：f(x)≈x，即约等于x。这样的好处是使得输出的幅值不会随着深度的增加而发生显著的增加，从而使网络更为稳定，同时梯度也能够更容易地回传。这个与非线性是有点矛盾的，因此激活函数基本只是部分满足这个条件。
8. 参数少：大部分激活函数都是没有参数的。像PReLU带单个参数会略微增加网络的大小。还有一个例外是Maxout，尽管本身没有参数，但在同样输出通道数下k路Maxout需要的输入通道数是其它函数的k倍，这意味着神经元数目也需要变为k倍；但如果不考虑维持输出通道数的情况下，该激活函数又能将参数个数减少为原来的k倍。
9. 归一化（normalization）：对应的激活函数是SELU，主要思想是使样本分布自动归一化到零均值、单位方差的分布，从而稳定训练。归一化的思想也被用于网络结构的设计，比如Batch Normalization。
此处的参考资料：https://www.zhihu.com/question/67366051/answer/262087707
激活函数
激活函数的发展经历了Sigmoid -> Tanh -> ReLU -> Leaky ReLU -> Maxout这样的过程，还有一个特殊的激活函数Softmax，因为它只会被用在网络中的最后一层，用来进行最后的分类和归一化。如果按照饱和与否作为区分条件，表示如下图：
sigmoid
非线性函数的数学公式：
导数性质：
![\sigma(x)' =\sigma (x) [1-\sigma (x)]](http://img.e-com-net.com/image/info8/00f3d3a50a02444bbc26f3df1a635077.gif){kind=small}
![{[\log\sigma (x)]}' = 1-\sigma (x)](http://img.e-com-net.com/image/info8/f5ed183cf922447e8f2180afec0a7691.gif){kind=small}
![{[\log(1-\sigma (x))]}' = -\sigma (x)](http://img.e-com-net.com/image/info8/869f8a22ba0a4549b5db3fa7dc939e02.gif){kind=small}
0到1范围内，适合输出为概率的情况，但是现在已经很少有人在构建神经网络的过程中使用sigmoid。
缺点：
Sigmoid函数饱和使梯度消失。当神经元的激活在接近0或1处时（非常大或者非常小）会饱和，在这些区域梯度几乎为0，导致梯度消失，几乎没有信号通过神经传回上一层。
Sigmoid函数的输出不是关于原点对称的。因为如果输入神经元的数据总是正数，那么关于的梯度在反向传播的过程中，将会要么全部是正数，要么全部是负数，这将会导致梯度下降权重更新时出现z字型的下降。
计算exp比较耗时。
Tanh
Tanh非线性函数的数学公式是
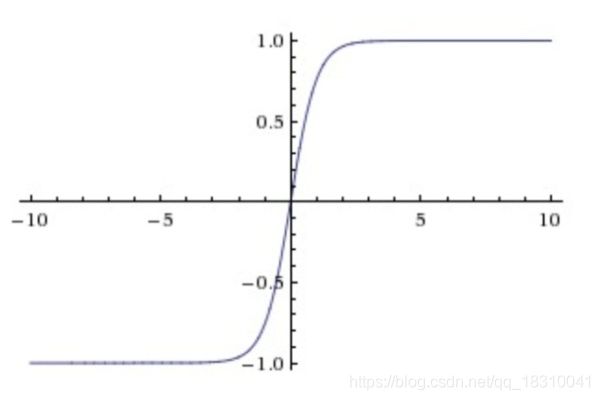
Tanh非线性函数将实数值压缩到[-1,1]之间。
优点：
Tanh解决了Sigmoid的输出是不是零中心的问题
缺点：
仍然存在饱和问题。为了防止饱和（梯度为0），会在激活函数前多做一步batch normalization，尽可能保证每一层网络的输入具有均值较小的、零中心的分布。
ReLU
优点：
相较于sigmoid和tanh函数，ReLU对于随机梯度下降的收敛有巨大的加速作用；sigmoid和tanh在求导时含有指数运算，而ReLU只需要一个阈值就可以得到激活值，求导几乎不存在任何计算量。
对比sigmoid类函数主要变化是：
1）单侧抑制；
2）相对宽阔的兴奋边界；
3）稀疏激活性。
缺点：
ReLU单元比较脆弱并且可能“死掉”，而且是不可逆的，因此导致了数据多样化的丢失。通过合理设置学习率，会降低神经元“死掉”的概率。举个例子：一个非常大的梯度流过一个 ReLU 神经元，更新过参数之后，这个神经元再也不会对任何数据有激活现象了，因此一定要小心设置 learning rate！
Leaky ReLU：
解决“dying ReLU” 的问题，
修正了数据分布，又保留了一些负轴的值，使得负轴信息不会全部丢失。 的范围是1到正无穷，论文中作者建议设置为一个较大的数，比如100.
Parametric ReLU：
对于 Leaky ReLU 中的 ，是先验知识的人工赋值。如果 =0，那么 PReLU 退化为 ReLU；如果 是一个很小的固定值（=0.01），则 PReLU 退化为 Leaky ReLU
通过反向传播来学习，BP 更新 时，采用的是带动量的更新方式，下式的两个系数分别是动量和学习率：
论文：https://arxiv.org/pdf/1502.01852.pdf
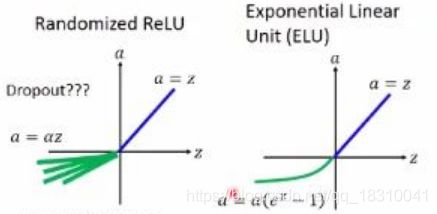
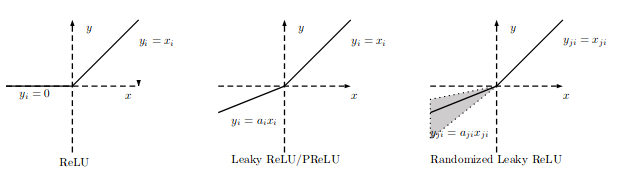
Randomized ReLU：
来自于Kaggle NDSB Competition，RReLU的亮点在于，在训练过程中，aji是从均匀分布 U(I,u) 中抽取的随机数。形式如下：
在测试过程中，采用所有训练的平均数，我们使用：
论文：https://arxiv.org/pdf/1505.00853.pdf
ELUs
负半轴不再是线性的输出，而是一个指数函数。其中引入了一个参数α，也就是当输入趋近于负无穷时，输出是-α。
Maxout
仿照dropout的思想，dropout使每个输入神经元以一定的概率不工作，而maxout更极端的则是对上一层的多个feature map跨通道取最大值作为输出。
使用maxout的默认先验：样本集是凸集可分的
Maxout在网络中充当激活函数的作用，激活函数的一个特点是非线性，这样可以使网络逼近任意的函数，而Maxout是一个分段函数，如下图所示，每个激活函数都可以通过Maxout在局部空间内取最大值得到。
优点：
Maxout具有ReLU的优点，如计算简单，不会 saturation饱和，同时又没有ReLU的一些缺点，如容易死掉。
缺点：
每个神经元的参数double，这就导致整体参数的数量激增。
论文：https://arxiv.org/pdf/1302.4389.pdf
代码：https://github.com/lisa-lab/pylearn2/tree/master/pylearn2/scripts/papers/maxout