《剑指offer》题解——week2（持续更新）

❤ 作者主页：Java技术一点通的博客
❀ 个人介绍：大家好，我是Java技术一点通！(￣▽￣)~*
❀ 微信公众号：Java技术一点通
记得点赞、收藏、评论⭐️⭐️⭐️
认真学习!!!

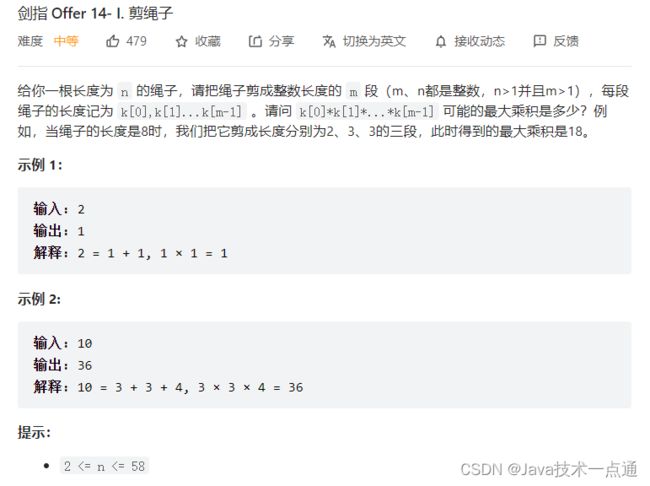
一、剑指 Offer 14- I. 剪绳子

1. 题目描述

2. 思路分析

思路一： 动态规划 f[i] = max(f[i], max(j * (i - j), j * f[i - j]))

1. f[i]表示长度为i的绳子剪成m段后的最大乘积，初始化f[2] = 1;
2. 我们先把绳子剪掉第一段（长度为j），如果只剪掉长度为1，对最后的乘积无任何增益，所以从长度为2开始剪;
3. 剪了第一段后，剩下(i - j)长度可以剪也可以不剪。如果不剪的话长度乘积即为j * (i - j)；如果剪的话长度乘积即为j * f[i - j]。取两者最大值max(j * (i - j), j * f[i - j]);
4. 第一段长度j可以取的区间为[2,i)，对所有j不同的情况取最大值，因此最终f[i]的转移方程为
   f[i] = max(f[i], max(j * (i - j), j * f[i - j]));
5. 最后返回f[n]即可。

思路二： 贪心
核心思路是：尽可能把绳子分成长度为3的小段，这样乘积最大

1. 如果 n == 2，返回1，如果 n == 3，返回2，两个可以合并成n小于4的时候返回n - 1;
2. 如果 n == 4，返回4
3. 如果 n > 4，分成尽可能多的长度为3的小段，每次循环长度n减去3，乘积res乘以3；最后返回时乘以小于等于4的最后一小段;
4. 以上2和3可以合并。

3. 代码实现

思路一代码：

class Solution {
public:
    int cuttingRope(int n) {
        vector f(n + 1);
        f[2] = 1;
        for (int i = 3; i <= n; i ++ ) {
            for (int j = 2; j < i; j ++ ) {
                f[i] = max(f[i], max(j * (i - j), j * f[i - j]));
            }
        }
        return f[n];
    }
};

思路二代码：

class Solution {
public:
    int cuttingRope(int n) {
        if (n < 4) return n - 1;
        int res = 1;
        while (n > 4) {
            res *= 3;
            n -= 3;
        }
        return res * n;
    }
};

 
 

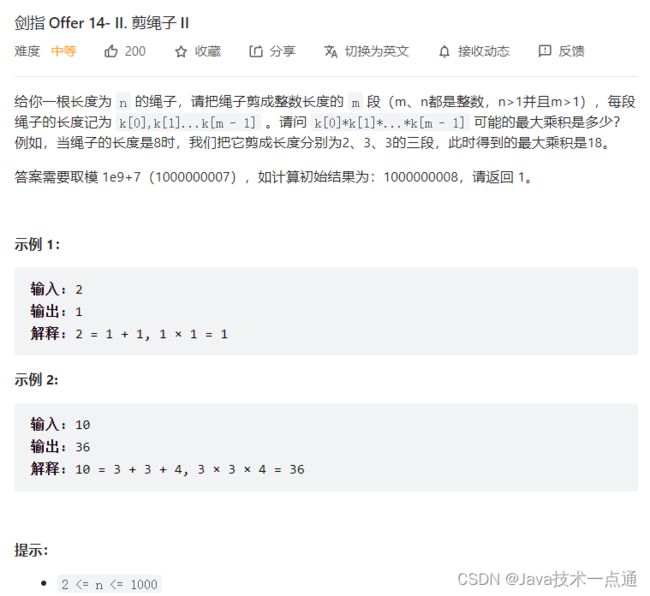
二、剑指 Offer 14- II. 剪绳子 II

1. 题目描述

2. 思路分析

由于需要对结果进行取余，导致不能使用动态规划，因为取模导致了dp的运算出现了问题。dp是通过最优子问题来计算出最终结果的，而取模之后就导致计算最优子问题出现了问题，计算出来的dp[i-j]*j表面上可能是最大的，但是dp[i-j]也是经过取模运算的，从而这会导致dp[i]不是由前面的最优子问题推出来的。
因此，使用dp时，前面的结果不能取余，要保留完整的值来进行比较，通过比较确定最优的子问题结果。
因此本题通过贪心算法来实现，最后对结果取余即可。

3. 代码实现

class Solution {
public:
    int cuttingRope(int n) {
        if (n < 4) return n - 1;
        long res = 1;
        while (n > 4) {
            res = res * 3 % 1000000007;
            n -= 3;
        }
        return res * n % 1000000007;
    }
};

 
 

三、剑指 Offer 15. 二进制中1的个数

1. 题目描述

2. 思路分析

使用lowbit操作，每次lowbit操作截取一个数字最后一个1后面的所有位，每次减去lowbit得到的数字，直到数字减到0，就得到了最终1的个数。
例如：0000100100经过lowbit操作后就会取出最后一个1后面的所有位，即100。

3. 代码实现

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int res = 0;
        for (uint32_t i = n; i; i -= i & -i) res ++;
        return res;
    }
};

 
 

四、剑指 Offer 16. 数值的整数次方

1. 题目描述

2. 思路分析

求 $x^n$ 最简单的方法是通过循环将 n 个 x 乘起来，依次求 $x^1$, $x^2$, ……, $x^{n-1}$,$x^n$，时间复杂度是O(n)。
快速幂法 可将时间复杂度降低至 O($lo{g}_2$ n)。

• 对于任何十进制正整数 nn ，设其二进制为"$b_m$…$b_3$$b_2$$b_1$"($b_i$为二进制某位值， i ∈ [1, m])，则有：

  1. 二进制转十进制： n = 1$b_1$ + 2$b_2$ + 4$b_3$ + …… + $2^{m-1}$$b_m$（即二进制转十进制公式）；
  2. 幂的二进制展开： $x^n$ = $x^{1b_1+2b_2+4b_3+\dots +2^{m-1}{b}_m}$ = $x^{1b_1}$$x^{2b_2}$$x^{4b_3}$…$x^{2^{m-1}{b}_m}$；

• 根据以上推导，可把计算 $x^n$转化为解决以下两个问题：

  • **计算$x^1$, $x^2$, $x^4$, …, $x^{2^{m-1}}$的值：**循环赋值操作 x = $x^2$即可；
  • **获取二进制各位$b_1$, $b_2$, $b_3$, …, $b_m$的值：**循环执行以下操作即可：
    1. n & 1 (与操作)： 判断 n 二进制最后一位是否是 1 ；
    2. n >> 1 (移位操作)： n 右移一位（可理解为删除最后一位）。

 

• 因此，应用以上操作，可在循环中依次计算$x^{2^0{b}_1}$, $x^{2^1{b}_2}$,…,$x^{2^{m-1}{b}_m}$的值，并将所有$x^{2^{i-1}{b}_i}$累计相乘即可。
  • 当 $b_i$ = 0时： $x^{2^{i-1}{b}_i}$ = 1；
  • 当 $b_i$ = 1时： $x^{2^{i-1}{b}_i}$ = $x^{2^{i-1}}$；

但还是有一些小细节要注意的：

• 如果质数是负数的话，要先把指数取绝对值，计算出来两个非负数的绝对值再取倒数。
• int的范围是−2147483648 ~ 2147483647，对−2147483648取绝对值会爆掉。

 

3. 代码实现

class Solution {
public:
    double myPow(double x, int n) {
        if (x == 0) return 0;
        long b = n;
        double res = 1.0;
        if (b < 0) {
            x = 1 / x;
            b = -b;
        }
        while (b) {
            if ((b & 1) == 1) res *= x;
            x *= x;
            b >>= 1;
        }
        return res;
    }
};

 
 

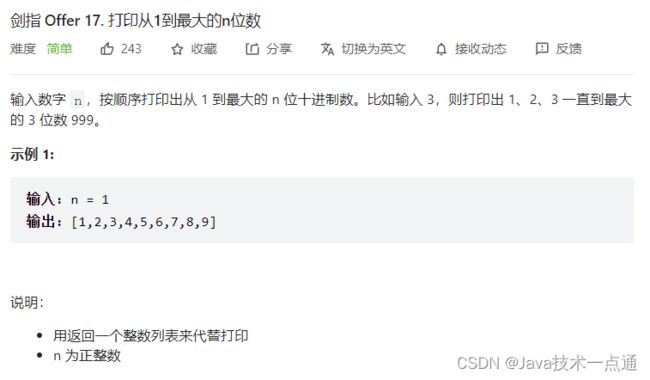
五、剑指 Offer 17. 打印从1到最大的n位数

1. 题目描述

2. 思路分析

题目要求打印 “从 1 至最大的 n 位数的列表” ，因此需考虑以下两个问题：

1. 最大的n位数（记为 end ）和位数 n 的关系： 例如最大的 1 位数是 99 ，最大的 2 位数是 99 ，最大的 3 位数是 999 。则可推出公式：end = $10^n-1$
2. 大数越界问题： 当 n 较大时，end 会超出 int32 整型的取值范围，超出取值范围的数字无法正常存储。但由于本题要求返回 int 类型数组，相当于默认所有数字都在 int32 整型取值范围内，因此不考虑大数越界问题。

不考虑大数打印解法： 暴力枚举
只需定义区间 [1, $10^n$ - 1] ，通过 for 循环生成结果列表 res 并返回即可。

考虑大树打印解法： 递归生成全排列
基于分治算法的思想，先固定高位，向低位递归，当个位已被固定时，添加数字的字符串。例如当 n=2 时（数字范围 1 - 99 ），固定十位为 0 - 9 ，按顺序依次开启递归，固定个位 0 - 9 ，终止递归并添加数字字符串。
防止大数越界，通过字符串来存贮答案，由于本题要求输出为int类型，因此最后再将string转化为int。

3. 代码实现

不考虑大数打印解法：

class Solution {
public:
    vector printNumbers(int n) {
        int end = pow(10, n) - 1;
        vector res;
        for (int i = 1; i <= end; i ++ ) 
            res.push_back(i);
        return res;
    }
};

考虑大数打印解法：

class Solution {
public:

    vector res;
    string path;
    char s[10] = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};

    void dfs(int u, int len) {
        if (u == len) {
            res.push_back(path);
            return;
        }
        int start = u==0? 1 : 0;  // u=0表示左边第一位数字，不能为0
        for (int i = start; i < 10; i ++ ) {
            path.push_back(s[i]);
            dfs(u + 1, len);
            path.pop_back();
        }

    }

    vector printNumbers(int n) {
        for (int i = 1; i <= n; i ++ ) 
            dfs(0, i);

        // 将string转化为int
        vector res_int;
        for (int i = 0; i < res.size(); i ++ ) 
            res_int.push_back(stoi(res[i]));
        return res_int;
    }
};

 
 

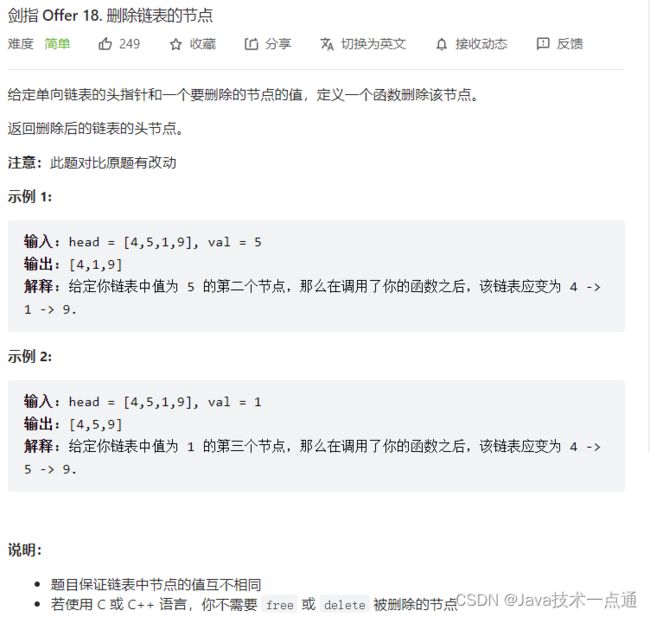
六、剑指 Offer 18. 删除链表的节点

1. 题目描述

2. 思路分析

本题删除值为val 的节点分需为两步：定位节点、修改引用。

1. 定位节点： 遍历链表，直到 head.val == val 时跳出，即可定位目标节点。
2. 修改引用： 设节点 cur 的前驱节点为 pre ，后继节点为 cur.next ；则执行 pre.next = cur.next ，即可实现删除 cur 节点。

算法步骤：

1. 特例处理： 当应删除头节点 head 时，直接返回 head.next 即可。
2. 初始化： pre = head , cur = head.next 。
3. 定位节点： 当 cur 为空 或 cur 节点值等于 val 时跳出。
4. ** 删除节点：** 若 cur 指向某节点，则执行 pre.next = cur.next ；若 cur 指向 null ，代表链表中不包含值为 val 的节点。
5. 返回值： 返回链表头部节点 head 即可。

3. 代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* deleteNode(ListNode* head, int val) {
        if (head->val == val) return head->next;
        ListNode * pre = head, *cur = head->next;
        while (cur != NULL && cur->val != val) {
            pre = cur;
            cur = cur->next;
        } 
        if (cur != NULL) pre->next = cur->next;
        return head;
    }
};

 
 

七、剑指 Offer 19. 正则表达式匹配

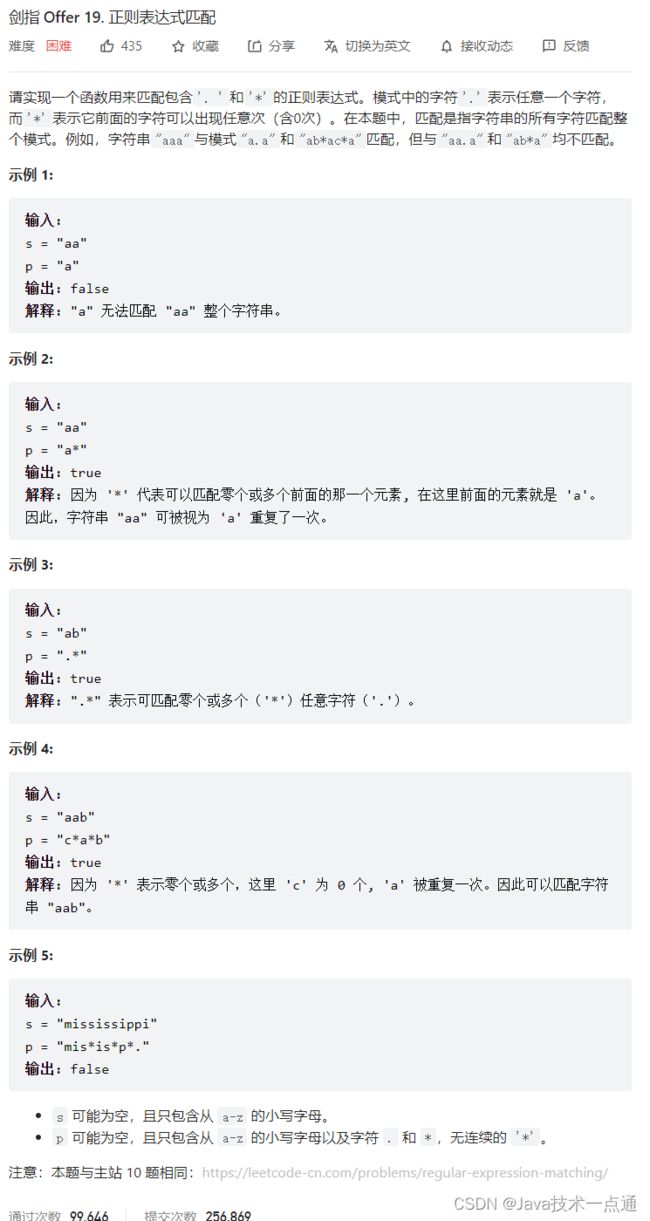
1. 题目描述

2. 思路分析

动态规划：

• 状态定义： 设动态规划矩阵 dp ， dp[i][j] 代表字符串 s 的前 i 个字符和 p 的前 j 个字符能否匹配。
• 转移方程： 需要注意，由于 dp[0][0] 代表的是空字符的状态， 因此 dp[i][j]对应的添加字符是 s[i - 1] 和 p[j - 1] 。

1. 当 p[j - 1] = '*' 时， dp[i][j] 在当以下任一情况为 true时等于 true ：
   1. dp[i][j - 2]： 即将字符组合 p[j - 2] * 看作出现 0 次时，能否匹配；
   2. dp[i - 1][j] 且 s[i - 1] = p[j - 2]: 即让字符 p[j - 2] 多出现 1 次时，能否匹配；
   3. dp[i - 1][j] 且 p[j - 2] = '.': 即让字符 '.' 多出现 1 次时，能否匹配；
2. 当 p[j - 1] != '*' 时， dp[i][j] 在当以下任一情况为 true时等于true ：
   1. dp[i - 1][j - 1] 且 s[i - 1] = p[j - 1]： 即让字符 p[j - 1] 多出现一次时，能否匹配；
   2. dp[i - 1][j - 1] 且 p[j - 1] = '.'： 即将字符 . 看作字符 s[i - 1] 时，能否匹配；

• 初始化： 需要先初始化 dp 矩阵首行，以避免状态转移时索引越界。

  1. dp[0][0] = true： 代表两个空字符串能够匹配。
  2. dp[0][j] = dp[0][j - 2] 且 p[j - 1] = '*'： 首行 s 为空字符串，因此当 p 的偶数位为 * 时才能够匹配（即让p的奇数位出现 0 次，保持 p 是空字符串）。因此，循环遍历字符串 p ，步长为 2（即只看偶数位）。

• 返回值： dp 矩阵右下角字符，代表字符串 s 和 p 能否匹配。

 

3.代码实现

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.size() + 1, n = p.size() + 1;
        vector> dp(m, vector(n, false));
        dp[0][0] = true;
        // 初始化首行
        for(int j = 2; j < n; j += 2)
            dp[0][j] = dp[0][j - 2] && p[j - 1] == '*';
        // 状态转移
        for(int i = 1; i < m; i++) {
            for(int j = 1; j < n; j++) {
                if(p[j - 1] == '*') {
                    if(dp[i][j - 2]) dp[i][j] = true;                              // 1.
                    else if(dp[i - 1][j] && s[i - 1] == p[j - 2]) dp[i][j] = true; // 2.
                    else if(dp[i - 1][j] && p[j - 2] == '.') dp[i][j] = true;      // 3.
                } else {
                    if(dp[i - 1][j - 1] && s[i - 1] == p[j - 1]) dp[i][j] = true;  // 1.
                    else if(dp[i - 1][j - 1] && p[j - 1] == '.') dp[i][j] = true;  // 2.
                }
            }
        }
        return dp[m - 1][n - 1];
    }
};

 
 

八、剑指 Offer 20. 表示数值的字符串

1. 题目描述

2. 思路分析

模拟、字符串处理

1. 先去除行首和行尾空格；
2. 行首如果有一个正负号，直接忽略；
3. 如果字符串为空或只有一个'.'，则不是一个合法数；
4. 循环整个字符串，去掉以下几种情况：
   （1）'.'或'e' 的个数多于1个；
   （2）'.'在'e' 的后面出现；
   （3）'e'后面或前面为空，或者'e'前面紧跟着'.'；
   （4）'e'后面紧跟着正负号，但正负号后面为空；
5. 剩下的情况都合法。

3. 代码实现

class Solution {
public:
   bool isNumber(string s) {
       int i = 0;
       while (i < s.size() && s[i] == ' ') i ++;
       int j = s.size() - 1;
       while (j >= 0 && s[j] == ' ') j --;
       if (i > j) return false;
       s = s.substr(i, j - i + 1);

       if (s[0] == '-' || s[0] == '+') s = s.substr(1);
       if (s.empty() || s[0] == '.' && s.size() == 1) return false;

       int dot = 0, e = 0;
       for (int i = 0; i < s.size(); i ++ ) {
           if (s[i] >= '0' && s[i] <= '9') ;
           else if (s[i] == '.') {
               dot ++;
               if (e || dot > 1) return false;
           }
           else if (s[i] == 'e' || s[i] == 'E') {
               e ++;
               if (i + 1 == s.size() || !i || e > 1 || i == 1 && s[0] == '.') return false;
               if (s[i + 1] == '+' || s[i + 1] == '-') {
                   if (i + 2 == s.size()) return false;
                   i ++;
               }
           }
           else return false;
       }
       return true;
   }
};

 
 

九、剑指 Offer 21. 调整数组顺序使奇数位于偶数前面

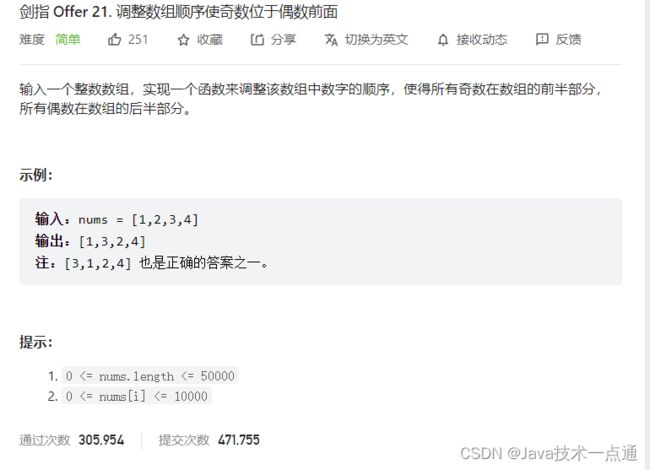
1. 题目描述

2. 思路分析

双指针算法：
用两个指针分别从首尾开始，往中间扫描。扫描时保证第一个指针前面的数都是奇数，第二个指针后面的数都是偶数。
每次迭代时需要进行的操作：

1. 第一个指针一直往后走，直到遇到第一个偶数为止；
2. 第二个指针一直往前走，直到遇到第一个奇数为止；
3. 交换两个指针指向的位置上的数，再进入下一层迭代，直到两个指针相遇为止；

3.代码实现

class Solution {
public:
    vector exchange(vector& nums) {
        int l = 0, r = nums.size() - 1;
        while (l < r) {
            while (l < r && nums[l] % 2 == 1) l ++;
            while (l < r && nums[r] % 2 == 0) r --;
            if (l < r) swap(nums[l], nums[r]);
        }
        return nums;
    }
};

 
 

十、剑指 Offer 22. 链表中倒数第k个节点

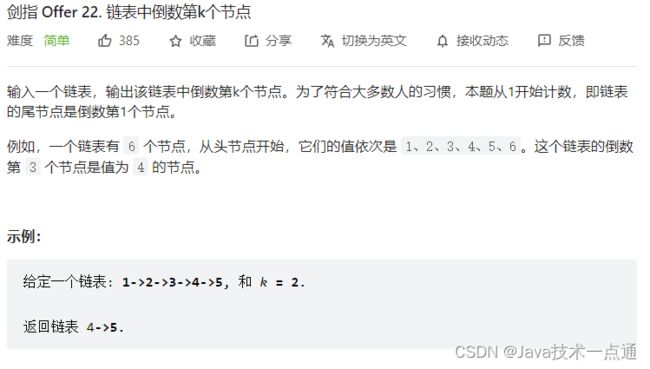
1. 题目描述

2. 思路分析

我们一共遍历两次：

1. 第一次遍历得到链表总长度 n；
2. 链表的倒数第 k 个节点，相当于正数第 n−k+1 个节点。所以第二次遍历到第 n−k+1 个节点，就是我们要找的答案。
   注意： 当 k>n 时要返回NULL。

3. 代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        int n = 0;
        for (auto p = head; p; p = p->next) n ++;
        if (n < k) return NULL;
        auto p = head;
        for (int i = 0; i < n - k; i ++ ) p = p->next;
        return p;
    }
};

 
 

十一、剑指 Offer 24. 反转链表

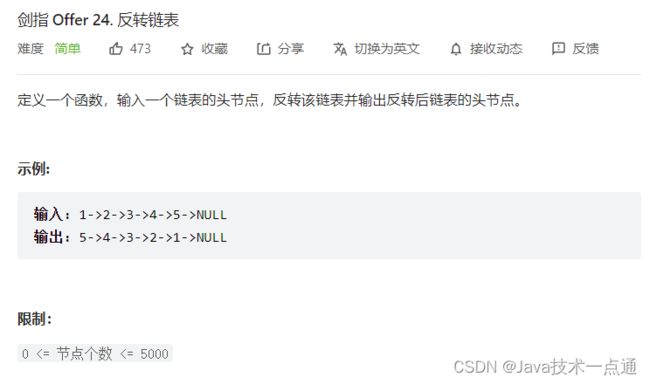
1. 题目描述

2. 思路分析

迭代（双指针）
翻转即将所有节点的next指针指向前驱节点。
由于是单链表，我们在迭代时不能直接找到前驱节点，所以我们需要一个额外的指针保存前驱节点。同时在改变当前节点的next指针前，不要忘记保存它的后继节点。

3. 代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode * prev = NULL;
        ListNode *cur = head;
        while (cur) {
            ListNode *tmp = cur->next;
            cur->next = prev;
            prev  = cur;
            cur = tmp;
        }
        return prev;
    }
};

 

创作不易，如果有帮助到你，请给题解点个赞和收藏，让更多的人看到！！！
关注博主不迷路，内容持续更新中。