排序算法1：归并排序的基本思想和应用示例

归并排序

1：归并排序基本思想

1：归并排序的过程：递归+合并
  递归：每一次将数组分为左右2个子数组，然后再将左右2个子数组划分为2个子数组。base是当划分的子数组只有1个数字时，就直接返回。返回了两个base的结果之后，然后进行合并操作。

  合并：首先最基础的base是，左边子数组返回只有1个数，右边子数组返回只有1个数，两个数之间可以比较大小排序。那么这时返回后，左边子数组有2个数，右边子数组有2个数；相应地，如果数组很长，那么之后是左边排序后是4个数，右边排好序后是4个数。。左8，右8。。

这个时候怎么较快地对左右进行合并后排好序呢？
  常用方法是使用双指针方法，即额外准备一个和左边子数组的长度（eg:4）与右边子数组的长度(eg:4)的和一样长的数组，即额外空间复杂度为8。然后左指针p指向左边子数组的第一个元素，右指针q指向右边子数组的第一个元素。
process:
 1）哪个指针指向的数小，则拷贝该数到新数组中，同时该指针指向下一个数；
 2）直到有一个左右中有一个子数组拷贝完了，则直接拷贝另一个子数组的所有元素到新数组中；
 3）最后再把新数组中的元素全部拷贝回原来数组的位置；
下面是具体的图的说明，该图使用了参考链接[1]中的图片：
第一步是递归：

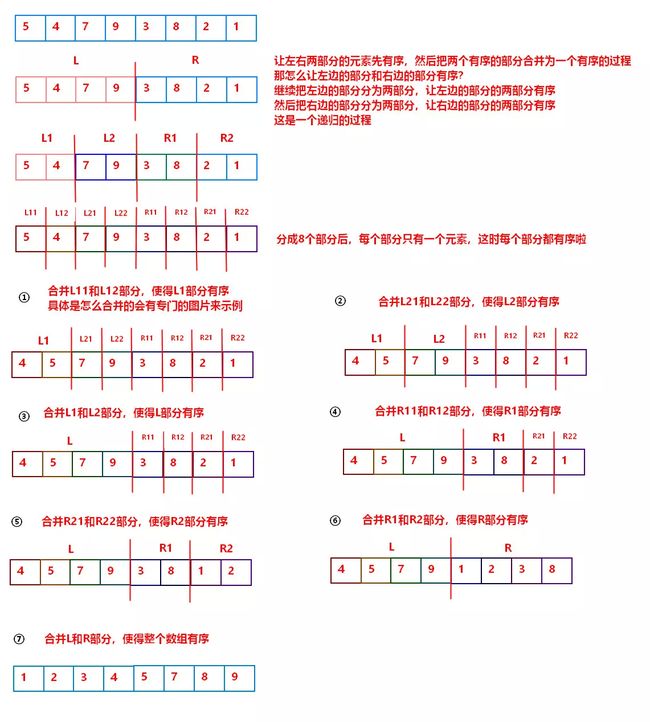
第二步是合并：

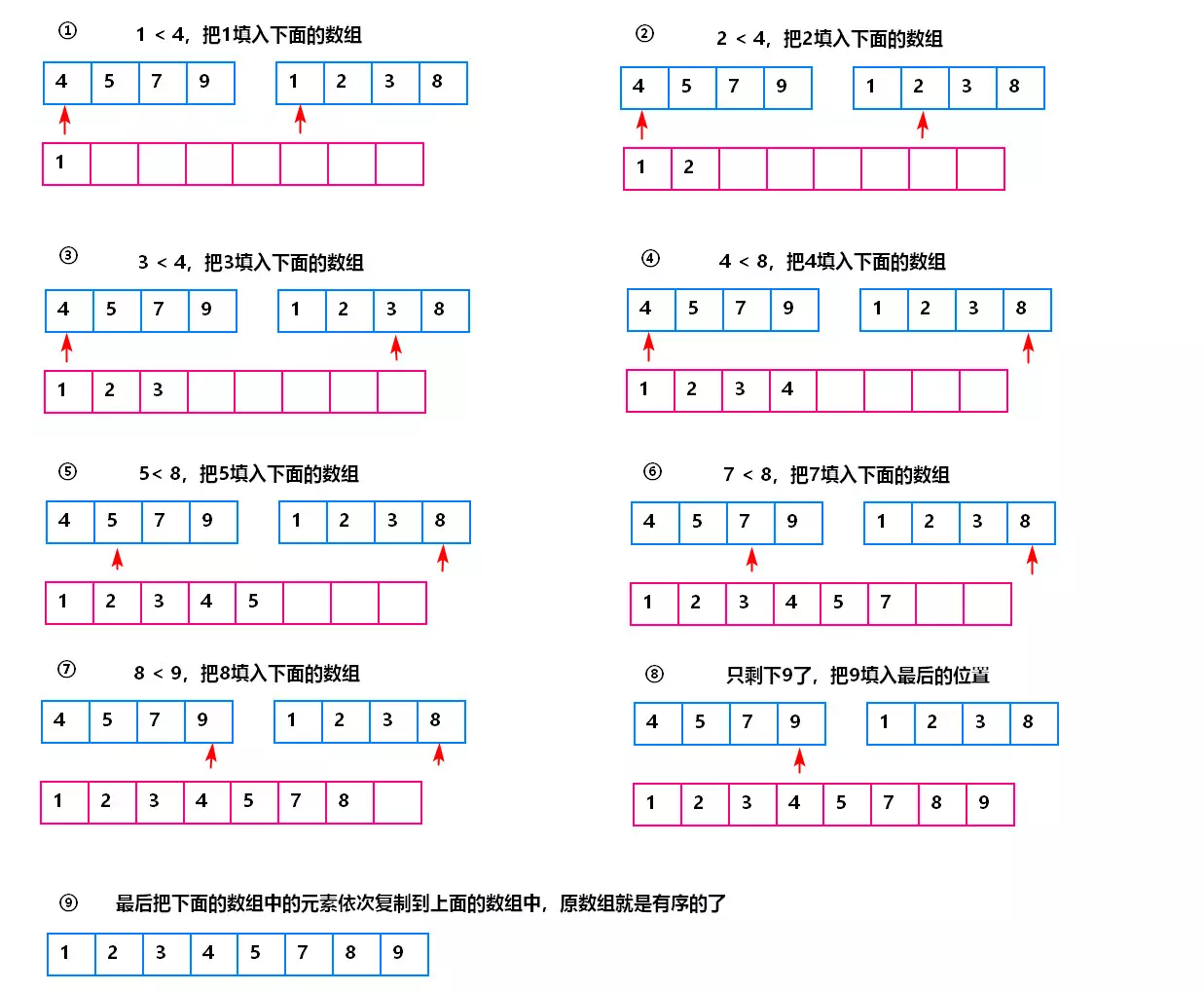
2：归并排序的应用：小和问题和逆序对问题

2.1 小和问题和逆序对问题

  小和问题：在一个随机数组中，找出左边比右边元素小的所有元素之和。
  逆序对问题：一个随机数组中，如果左边的数大，右边的数小，则称这两个数位一个逆序对。 求出一个数列中有多少个逆序对。
分析：
小和问题：
  归并排序在第二步合并的操作时，对于左边子数组有一个指针p，右边子数组有一个指针q。由于在两个子数组内部是有序的，所以如果p指针指向的元素小于q指针指向的元素，那么对于p指针所指向的值（eg:3）来说，从右边子数组的q指针到最后的所有元素的个数(eg:5)都肯定是大于p指针指向的值，所以此时对于这个3来说，小数和sum = sum + 3*5。
  具体可以参考下面的C++的代码。即对于左边子数组的p指针指向的值N，如果小于右边子数组的q指针指向的值M，那么右边子数组的q到右边子数组的边界Right就有(Right - p2 + 1)个N，所以有：

sum += arr[p1] < arr[p2] ? (right - p2 + 1) * arr[p1] : 0;  // 计算小数和

逆序对问题：
  同理，逆序对问题也是一样的性质，只是逆序对是当左边子数组的p指针指向的值N，大于右边子数组的q指针指向的值M时，形成了一对逆序对。同理这个时候应该是左边子数组的指针q到左边子数组的边界mid的所有元素都是大于q指针指向的值M的。具体的C++代码如下：

sum += arr[p1] > arr[p2] ? (mid - p1 + 1) : 0; 计算逆序对的对数 

2.2 C++的代码示例

2.2.1 main.c文件

#include 
#include 
#include 
#include "MergeSort.h"
using namespace std;

// 生成有n个元素的随机数组,每个元素的随机范围为[rangeL, rangeR] 闭区间
int *generateRandomArray(int n, int rangeL, int rangeR) {
    if (rangeL >= rangeR){
        cout << "lt is wrong!" << endl;
    }
	int *arr = new int[n]; // 创建一个 n个元素的数组

	srand(time(NULL)); // 随机种子
	for (int i = 0; i < n; i++)
	    arr[i] = rand() % (rangeR - rangeL + 1) + rangeL;
	return arr;
}

int main()
{
    int len = 15;
    int minnum = 0;
    int maxnum = 100;
    int *arr = generateRandomArray(len, minnum, maxnum);
    cout << "Orignal array:" << endl;
    for (int i=0; i<len; i++){
        cout << arr[i] << "   ";
    }
    cout << endl;
    int brr[len];
    for (int i=0; i<len; i++){
        brr[i] = arr[i];
    }

    //归并排序
    int* result =  MergeSortArr(brr, len);
    cout << "print the MergeSortArr result!" << endl;
    for (int i=0; i<len; i++){
        cout << result[i] << "   ";
    }
    cout << endl;

    return 0;
}
}

2.2.2 MergeSort.h头文件

#ifndef MERGESORT_H_INCLUDED
#define MERGESORT_H_INCLUDED
#endif // MERGESORT_H_INCLUDED
int* MergeSortArr(int arr[], int len);

2.2.3 MergeSort.cpp文件

#include 
#include "MergeSort.h"
using namespace std;

int Merge(int arr[],int left,int mid,int right){
	int * help = new int[right- left + 1];
	int p1 = left;
	int p2 = mid + 1;
	int i = 0;
	int sum = 0;
	while(p1 <= mid && p2 <= right){
		sum += arr[p1] < arr[p2] ? (right - p2 + 1) * arr[p1] : 0;  // 计算小数和
		//sum += arr[p1] > arr[p2] ? (mid - p1 + 1) : 0; 计算逆序对的对数
		help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
	}
	while(p1 <= mid){
		help[i++] = arr[p1++];
	}
	while(p2 <= right){
		help[i++] = arr[p2++];
	}
	for(int j = 0;j < i;j++){
		arr[left + j] = help[j];
	}
	delete []help;
	return sum;
}
int MergeSort(int arr[],int left,int right){
	if(left == right) return 0;
	int mid = left + ((right - left)>>1);
	return MergeSort(arr,left,mid) + MergeSort(arr,mid+1,right) + Merge(arr,left,mid,right);
}

int* MergeSortArr(int arr[], int len){
    cout << "####################" << endl;
    cout << "Begin to merge sort!" << endl;
    MergeSort(arr,0,len - 1);
    return arr;
}

2.2.4 结果展示
  由于初始无序数组是随机的，所以结果可能不会完全相同，仅作展示。

2.3 python代码示例

这里仅给出归并排序python代码的核心部分：

def merge_sort(items, le=lambda x, y: x <= y):
    """主函数体"""
    if len(items) <= 1:
        return items
    mid = len(items) // 2
    items1 = merge_sort(items[:mid], le)
    items2 = merge_sort(items[mid:], le)
    return merge(items1, items2, le)

def merge(items1: list, items2: list, le=lambda x, y: x <= y) -> list:
    """将两个有序列表合并为一个新的有序列表"""
    items3 = []
    index1, index2 = 0, 0
    while index1 < len(items1) and index2 < len(items2):
        if le(items1[index1], items2[index2]):
            items3.append(items1[index1])
            index1 += 1
        else:
            items3.append(items2[index2])
            index2 += 1
    items3 += items1[index1:]
    items3 += items2[index2:]
    return items3

def main():
    """执行函数"""
    items = [35, 12, 99, 18, 57, 66, 43, 32, 90]
    print('Orignal array:', items)
    print('Array after mergesort: ', merge_sort(items))
if __name__ == '__main__':
    main()

3：归并排序的时间复杂度、空间复杂度、稳定性

3.1 时间复杂度

  归并排序中每一次都进行2分递归调用，深度为O（logN），而归并操作中的常数操作为O（N），因此归并排序的时间复杂度是O（N*logN）

3.2 空间复杂度

  由于归并操作中，每一次要额外申请和所要排序数组一样长的数组空间，所以空间复杂度为O（N）

3.3 稳定性

  排序算法在归并操作中，当左边子数组的数等于右边子数组的数时，可以先复制左边子数组的数，所以是可以做成稳定的排序算法的。