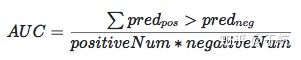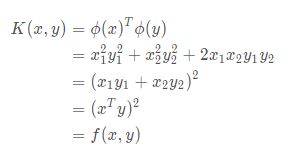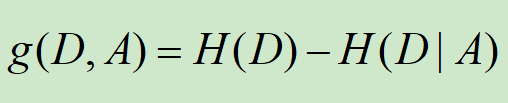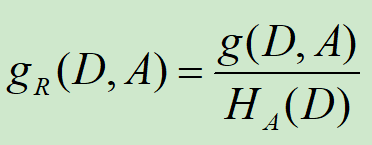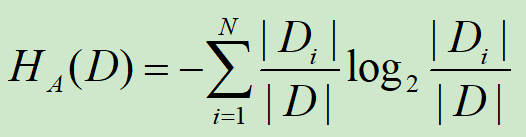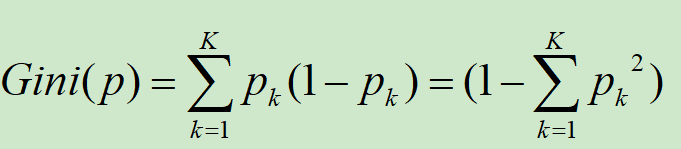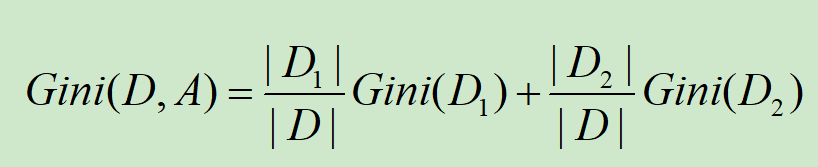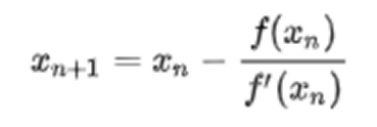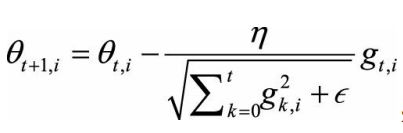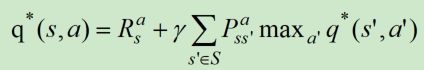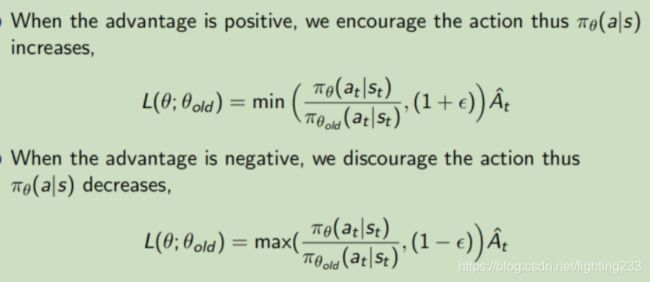机器学习、深度学习、强化学习

目录

机器学习

为什么MSE不适用于分类问题、交叉熵不适用于回归问题？

4、有哪些文本表示模型

5、图像分类任务中，训练数据不足会带来什么问题？如何缓解这个问题？

精确率与召回率的权衡

ROC曲线

14、ROC曲线相比于PR曲线有什么特点？

24、对于二分类问题，当训练集中正负样本非常不均衡时，如何处理数据来更好地训练分类模型？

15、比较LR和GBDT，在什么情况下LR优于GBDT

正则化线性模型

SVM

支持向量机包含几种模型？

目标函数的由来？将目标函数转换为对偶问题的推导？

为什么要转换为对偶问题进行求解？求解的权重个数？

SVM里面的C是啥？

SVM与LR之间的关系？

核函数原理

SVM和adaboost有什么联系？

决策树

C4.5：使用了信息增益比（越大越好）

CART：分类树使用基尼系数（越小越好）

深度学习

为什么CNN中的卷积核一般都是奇数✖️奇数

强化学习

1、强化学习和监督学习以及非监督学习的区别

2、如果问题不满足马尔科夫性怎么办，当前时刻的状态和它之前的很多状态有关。

3、强化学习中的过拟合问题

4、强化学习的损失函数是什么，和深度学习的损失函数有何关系？

5、简述DP、MC和TD的关系

6、求解MDP有哪些方法，有模型用什么方法，动态规划是什么？

7、MC、TD谁的方差大，为什么？

8、RL中基于值函数的和基于PG算法的优缺点以及适用场景

9、有模型RL算法和无模型RL算法的区别

10、确定性策略和随机性策略

11、RL中on-policy以及off-policy策略的区别，以及有哪些off-policy的方式

12、为什么有时候off-policy需要与重要性采样结合使用？

13、重要性采样的作用？

14、为什么Q-learning算法（或者DQN）作为off-policy可以不用重要性采样？

15、Sarsa算法像是在进行值函数估计，为什么能够收敛到最优策略？

16、sarsa和qlearning区别 哪个谨慎 为什么

17、策略迭代和值迭代的区别？

18、不打破数据相关性，神经网络的训练效果为什么就不好？

19、DQN采用了两个关键的trick是什么？

20、DDQN对DQN的改进？

21、有哪些方法可以使得RL训练稳定？

22、常见的平衡探索与利用的方法

23、A2C中的advantage function 和DQN中的advantage function 有什么区别？

24、Actor、Critic两者的区别是什么？

25、actor-critic框架中的critic起了什么作用？

26、策略梯度中的基线（baseline）如何确定？

27、为什么baseline可以直接减去一个值而对策略迭代没有影响？

28、DDPG是on-policy还是off-policy，为什么？

29、A3C是on-policy，为什么？

30、DDPG与A3C的区别？

31、GAE中两个参数哪个控制偏差，哪个控制方差？

32、TRPO、PPO都是on-policy的

A3C（Asynchronous Advantage Actor-Critic）

多臂赌博机

---

        

机器学习

为什么MSE不适用于分类问题、交叉熵不适用于回归问题？

sigmod函数，其导数为

MSE损失函数为，其中，

则其导数为，可以看出在使用MSE的时候，w,b的梯度都与sigmod函数对z的偏导有关系，而sigmod函数的偏导在自变量非常大或者非常小的时候，偏导数会接近于0，这将导致w、b的梯度不会发生变化，即梯度消失。而使用交叉熵时，不会出现上述问题，所以MSE不适用于分类问题。

MSE对于每一个输出的结果都非常看重，这会让错误的分类变的平均，不适合实际的分类问题，而交叉熵只对正确分类的结果看重。

https://www.cnblogs.com/USTC-ZCC/p/13219281.html

4、有哪些文本表示模型

词袋模型：将文本以词为单位划分开，每篇文章可以表示成一个长向量，向量中的每一维代表一个单词，而该维对应的权重（TF-IDF来计算）反映了这个词在文章中的重要程度。

N-gram模型：将连续出现的n个词组成的词组（N-gram）作为一个单独的特征放到向量表征中去。

5、图像分类任务中，训练数据不足会带来什么问题？如何缓解这个问题？

会产生过拟合的问题，处理方法分为两种：1、基于模型的方法，包括简化模型、添加正则项（L1,L2）、集成学习、dropout超参数等； 2、基于数据的方法，主要通过数据扩充，如随机旋转、平移、加噪声扰动、颜色变换、改变图像的亮度、对比度等等。此外，还可以借助其他的模型或者数据来进行迁移学习。（微调）

精确率与召回率的权衡

精确率是指分类正确的正样本个数占分类器判定为正样本个数（把正类预测为正类+把负类预测为正类）的比例，P=TP/(TP+FP)，而召回率是指分类正确的正样本个数占真正的正样本个数的比例，R=TP/(TP+FN)。在排序问题中，采用top N返回结果的precision值和recall值来衡量模型的性能。即认为模型返回的top N的结果就是模型判定的正样本，然后计算前N个位置上的准确率和前N个位置上的召回率。

Precision与recall是既矛盾又统一的两个指标。

P-R曲线能够反映一个排序模型的性能。此外，F1 score和ROC曲线也能综合反映一个排序模型的性能。F1 score是精确率与召回率的调和平均值：

F1 = (2*precision*recall)/(precision + recall)

F1分数让两者同时达到最高，取一个平衡。

ROC曲线

        ROC曲线横轴为FPR假阳性（所有实际为阴性的样本中，被错误地判定为阳性的比率FPR = FP/(TN+FP)），纵轴为TPR真阳性（所有实际为阳性的样本中，被正确判定为阳性的比率 TPR = TP/(TP+FN)）。因此，FPR和TPR都是只关心各自负样本和正样本中有多少被错误覆盖和正确覆盖的，所以，ROC曲线在正负样本比例变化时，没有影响。

在二分类问题中，模型的输出一般都是预测样本为正例的概率，通常需要指定一个阈值，当预测概率大于这个阈值时，样本就被判为正例。通过不断调整这个阈值，不断的得到(FPR, TPR)，就能绘制出曲线。

AUC是ROC曲线下的面积大小，计算AUC只需要沿着横轴积分即可。AUC越大说明分类器越可能把正样本放在前面，分类性能越好。

AUC的另一种定义是，分别随机从正负样本集中，抽取一个正样本、一个负样本，正样本的预测概率值比负样本的预测概率值还要大的可能性就是AUC的值。

则假设有（m+n）个样本，其中正样本m个，负样本n个，总共有m*n对，正样本预测为正样本的概率值大于负样本预测为正样本的概率值记为1，若正样本的预测概率等于负样本的预测概率，则加0.5，然后累加计数，再除以（m*n），就是AUC的值。

14、ROC曲线相比于PR曲线有什么特点？

        ROC曲线在正负样本的分布发生变化时，其曲线的形状能够基本保持不变，而PR曲线的形状一般会剧烈变化。这一特点让ROC曲线能够尽量降低不同测试集带来的干扰，更加客观地衡量模型本身的效果。而如果是想看在特定测试集上的效果，PR曲线更为的直观。

        AUC的优化目标是希望同时优化TPR和FPR，F1的目标是希望同时优化recall和precision。两者的共同点是TPR=Recall，即两者都希望将样本中实际为真的样本检测出来。

        不同之处在于，AUC还希望降低非真样本呈阳性的比例（假阳性），也就是检验犯错误的概率，即尽量不误报，保守估计。

        而F1则是希望提高检测为阳性的样本中实际为真的比例，即精确率，即希望不放过任何可能的样本，激进估计。

        因此，在预测传染病这种实际问题时，倾向于选择F1，而对于推荐场景中，担心用户的流失，更适合用AUC。

24、对于二分类问题，当训练集中正负样本非常不均衡时，如何处理数据来更好地训练分类模型？

分类模型在训练数据不均衡时会出现问题的本质原因是：模型在训练时优化的目标函数和人们在测试时使用的评价标准不一致。

一般从两个角度来处理样本不均衡问题。

• 基于数据的方法

对数据进行重采样，使得样本变的均衡。

最简单的方法是随机采样，分为过采样和欠采样。随机过采样（过分采样，少数变多）是从少数类样本集中随机重复抽取样本（有放回）以得到更多的样本；而随机欠采样则是从多数类样本集中随机选取较少的样本。

        直接的随机采样会带来一些问题，如过采样会对少数样本进行了多次复制，扩大了数据规模，增加了模型复杂度，容易过拟合。而欠采样会导致一些样本的缺失，造成模型只学习到整体模式的一部分。因此，通常在过采样时采用一些新的方法来产生新样本。例如SMOTE算法对少数类样本集中每个样本x，从它在样本集中的K近邻中随机选择一个样本y，然后在连线上随机选择一个点作为新合成的样本点。

        对于欠采样，可以采用Informed Undersampling算法来解决由于随机欠采样带来的数据丢失问题。常见的Informed Undersampling有easy ensemble算法和balance cascade算法，都是采用了集成学习机制。

        easy ensemble：将多数类样本随机划分成n个子集，每个子集的数量等于少数类样本的数量，这相当于欠采样。接着将每个子集与少数类样本结合起来分别训练一个模型，最后将n个模型集成，这样虽然每个子集的样本少于总体样本，但集成后总信息量并不减少。

        balance cascade：类似于boosting的形式，在第n轮训练中，将从多数类样本中抽样得来的子集与少数类样本结合起来训练一个基学习器H，训练完后多数类中能被H正确分类的样本会被剔除。在接下来的第n+1轮中，从被剔除后的多数类样本中产生子集用于与少数类样本结合起来训练，最后将不同的基学习器集成起来。

• 基于算法的方法

通过改变模型训练时的损失函数（如不同类别有不同的权重）；或者当样本极其不均衡时，也可以将问题转化为单类学习、异常检测等。

15、比较LR和GBDT，在什么情况下LR优于GBDT

        LR是线性模型，可解释性强，很容易并行化，但是学习能力有限，需要大量的人工特征工程。

        GBDT是非线性模型，具有天然的特征组合优势，特征表达能力强，但是树与树之间无法并行训练，而且树模型很容易过拟合。

        当在高维稀疏特征下，LR的效果一般会比GBDT好，LR等线性模型的正则项是对权重的惩罚；而树模型的惩罚项通常是叶子节点数和深度。带正则项的线性模型比较不容易对稀疏特征过拟合。

正则化线性模型

        对于线性模型，正则化通常是通过约束模型的权重来实现的。

岭回归

        是线性回归的正则化版本，将等于的正则化项加入到loss function中，是的学习算法不仅拟合数据 ，而且还使得模型权重尽可能小。

岭回归成本函数：J(θ) = MSE(θ) + α1/2∑θi2

Lasso回归

        Lasso回归成本函数：J(θ) = MSE(θ) + α∑|θi|；线性回归的另一种正则化叫做最小绝对收敛和选择算子回归（lasso 回归），添加的正则化项是权重向量的L1范数，而不是岭回归中L2范数的一半。

弹性网络

        弹性网络是介于岭回归和 Lasso 回归之间的中间地带。正则项是岭和 Lasso 正则项的简单混合，你可以控制混合比r。当 r=0 时，弹性网络等效于岭回归，而当r=1时，弹性网络等效于Lasso回归。

弹性网络成本函数：J(θ) = MSE(θ) + rα∑|θi| + 1-r)/2α(∑θi2

SVM

什么是支持向量？

        离划分超平面最近的数据点，是最难分类的点。

支持向量机包含几种模型？

        主要是根据训练数据集是否线性可分以及是否允许出现分类错误来进行划分。

1、硬间隔SVM：当训练数据线性可分时，硬间隔最大化不允许出现分类错误，此时超平面将所有训练数据集都分类正确，所以叫硬间隔支持向量机。

2、软间隔SVM：当训练数据近似线性可分时，软间隔最大化允许出现分类错误，此时超平面不能将所有训练数据点都分类正确，所以叫软间隔支持向量机。（松弛变量）

3、非线性SVM：当训练数据线性不可分时，通过使用核函数和软间隔最大化对数据进行分类。

目标函数的由来？将目标函数转换为对偶问题的推导？

 

为什么要转换为对偶问题进行求解？求解的权重个数？

        1、对偶问题往往更容易求解；（原问题是凸二次规划问题，转为对偶问题后，只用求解alpha系数，而alpha系数是只有支持向量才非0，其他全部为0）2、可以引入核函数，推广到非线性分类问题。

        求解的权重个数即为样本点的个数N。

SVM里面的C是啥？

        惩罚系数，类似于正则化项前面的系数。

SVM与LR之间的关系？

相同点：

        都是分类模型，本质上都是寻找最优分类超平面；

        都是监督学习；

        都是判别模型，即不关心数据是怎么生成的，只关心数据之间的差别，然后利用差别对数据进行分类。

        都可以增加不同的正则化项。

不同点：

        1、LR是统计方法，SVM是几何方法

        2、SVM 的处理方法是只考虑 Support Vectors，也就是和分类最相关的少数点去学习分类器。而逻辑回归通过非线性映射（sigmod函数）减小了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重；

        3、损失函数不同：LR 的损失函数是交叉熵，SVM 的损失函数是 HingeLoss，这两个损失函数的目的都是增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。对 HingeLoss 来说，其零区域对应的正是非支持向量的普通样本，从而所有的普通样本都不参与最终超平面的决定，这是支持向量机最大的优势所在，对训练样本数目的依赖大减少，而且提高了训练效率；

        4、LR 是参数模型，SVM 是非参数模型，参数模型的前提是假设数据服从某一分布，该分布由一些参数确定（比如正太分布由均值和方差确定），在此基础上构建的模型称为参数模型；非参数模型对于总体的分布不做任何假设，只是知道总体是一个随机变量，其分布是存在的（分布中也可能存在参数），但是无法知道其分布的形式，更不知道分布的相关参数，只有在给定一些样本的条件下，能够依据非参数统计的方法进行推断。所以 LR 受数据分布影响，尤其是样本不均衡时影响很大，需要先做平衡，而 SVM 不直接依赖于分布；

        5、LR 可以产生概率，SVM 不能；

        6、LR 不依赖样本之间的距离，SVM 是基于距离的；

        7、LR 相对来说模型更简单好理解，特别是大规模线性分类时并行计算比较方便。而 SVM 的理解和优化相对来说复杂一些，SVM 转化为对偶问题后，分类只需要计算与少数几个支持向量的距离，这个在进行复杂核函数计算时优势很明显，能够大大简化模型和计算。

核函数原理

        核函数主要是将数据映射到更高维度的空间，这个空间叫作特征空间。在特征空间中，数据能够更容易地分离或更好地结构化。是在低维空间进行内积计算。

        这种映射的形式也没有限制，甚至可以形成无限维空间。核函数表示特征空间的内积，通常表示为：

核函数通过内积计算，避免了直接计算映射。

假设存在二维向量x = [ x1 , x2 ] , y = [ y1 , y2 ]，将其升维(ϕ)到高维空间，则：

升维到三维空间：

则核函数的值为：

f 表示函数，在这里代表多项式核函数。在其他条件下，f 可以为任何函数形式。
升维到四维空间：

                                ​​​​​​​        

则核函数的值为：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        

这里要注意一个问题，当 ϕ (x) , ϕ (y) 是三维时，f(x,y) 可以化为三项的和；当 ϕ(x), ϕ(y) 是四维时，f 可以化为四项的和。所以 f 可以转化成多少项的和，ϕ(x),ϕ(y)就有多少维，即当f 可以化成无限的项相加时，ϕ(x),ϕ(y) 也可以是无限维的。高斯核可以数据扩展到无限维就是利用这个原理。

核函数的意义在于做到了没有真正映射到高维空间却达到了映射的作用，减少了大量的映射计算。

SVM和adaboost有什么联系？

        都不是一视同仁地看待所有样本，SVM仅取决于支持向量，而adaboost更关注之前被分错的样本。

决策树

ID3：使用信息增益来作为特征选取准则（越大越好）

信息增益：

C4.5：使用了信息增益比（越大越好）

使用信息增益存在着偏向于选取值较多的特征的问题，当一个属性可取值的数目较多时，可能在这个属性对应值下的样本只有一个或者很少个，此时它的信息增益会很高，ID3会认为这个特征适合划分，而实际上这会使得模型的泛化能力较差。

信息增益比:

特征A对训练数据集D的信息增益比gR(D, A)定义为其信息增益与训练数据集关于特征A的值的熵HA(D)之比。

n为特征A的取值个数。

CART：分类树使用基尼系数（越小越好）

基尼系数：在样本集合中，随机选择一个样本，其被分错的概率。基尼系数越小，数据集的纯度就越高，表示越不容易被分错。

假设有K类，样本点属于第k类的概率为pk，则概率分布的基尼系数为

若样本集根据特征A是否取某一可能值a被划分为D1和D2两部分，则在特征A的条件下，集合D的基尼系数为

Xgboost的损失函数是进行了二阶泰勒展开，为什么用二阶而不是三阶四阶？

        需要考虑到性能，一般二阶泰勒展开的近似效果已经很好了，没必要展开更高阶，而且更高阶的导数需要对损失函数有更高的要求，例如在回归问题中，MSE没有三阶以上的导数了（为0）。

深度学习

无约束优化问题的优化方法有哪些？

        1、直接法

        2、迭代法

                2.1 一阶法（梯度下降法）

                2.2 二阶法（牛顿法）

L1正则化使得模型参数具有稀疏性（0比较多）的原理是什么？

        

3x3卷积的优势

1、在保证具有相同的感知野的条件下，提升了网络的深度（层数），拥有了更多的非线性变换，在一定程度上提升了网络的效果。

2、减少了参数，两个3x3的和一个5x5的相比，参数量减少了一半。

1x1卷积核的作用

1. 调节通道数channel，因为1x1的卷积核不会改变height和width，改变的是通道数，使用多少个1x1的卷积核，输出的通道数就会变成多少。
2. 加入非线性，1x1的卷积核可以在保持特征图尺度不变的前提下大幅提升非线性特征（利用后接的非线性激活函数。
3. 跨通道信息
4. 减少参数，降维的时候就是减少了参数。

为什么CNN中的卷积核一般都是奇数✖️奇数

1. 奇数卷积核更加容易做padding，假设卷积核大小为k*k，为了让卷积后的图像大小与原图一样大，可得padding = (k-1)/2，因此，只有k取奇数，padding才能是整数。
2. 更容易找到中心点，在CNN中，一般以卷积核的某个基准点进行窗口滑动，通常这个基准点是卷积核的中心点，若k为偶数，则找不到中心点。

为什么使用relu激活函数

1. 采用sigmod等函数时，是指数运算，计算量大，反向传播求误差梯度时，求导计算量也大，而使用relu激活函数的计算量小。
2. 对于深层网络，sigmod函数反向传播时，很容易出现梯度消失的情况（sigmod接近饱和区时，变换太慢，导数趋于0，会造成信息丢失），从而无法完成深层网络的训练。
3. relu会使一部分神经元的输出为0，造成了网络的稀疏性，减少了参数的互相依存关系，缓解了过拟合问题的发生。

但是RELU也有局限性，因为在训练过程中会导致神经元死亡的问题，这是由于RELU函数f(x)=max(0,x)导致负梯度在经过该relu单元时被置为0，且在之后也不被任何数据激活，即流经该神经元的梯度永远为0，不对任何数据产生响应。在实际训练过程中，如果学习率设置较大，会导致超过一定比例的神经元不可逆死亡，从而参数梯度无法更新，训练失败。

因此，有人提出了relu的变种Leaky ReLU（LReLU），当z<0时，是一个斜率为a的线性函数，一般a为一个很小的正常数，但另一方面，a的选择又需要较强的人工先验或多次重复训练来确定合适的参数。

为此，人们又提出了PReLU（parametric ReLU），它将负轴的斜率a作为网络可学习的参数，与其他含参数网络层联合优化。

1. 梯度下降法沿着梯度的反方向？（梯度的反方向是函数值下降最快的方向）

解释1：泰勒展开公式

通过一阶泰勒展开式，利用线性近似和向量相乘最小化的思想。

根据一阶泰勒展开式，其中是微小矢量，大小是前进长度μ，μ为标量，设的单位向量用v表示，则=μv。

则有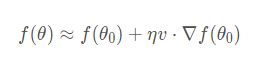，局部下降的目的是要让每次更新时，f()函数变小，则，因为μ为标量，所以，，要沿着梯度的反方向前进。

牛顿法

牛顿法：用来迭代求零点的方法，也可以用在最优化上。

        若要求f(x) = 0的解，则通过下面这个迭代公式来求解：

则若使用牛顿法来求解平方根：

其实就是对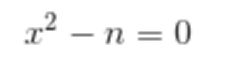求解，f(x) = x2-n, f’(x) = 2x。

class Solution:
    def mySqrt(self, x: int) -> int:
        if x==0:
            return 0
        c, x0 = float(x), float(x)
        while True:
            xi = 0.5*(x0+c/x0)
            if abs(x0-xi)<1e-7:   # 前后两次的更新幅度很小时
                break
            x0 = xi
        return int(x0)

优化器

adagrad：环境感知能力，采用了“历史梯度平方和”来衡量不同参数的梯度的稀疏性，取值越小表示梯度越稀疏，更新就应该越大。

momentum：动量

强化学习

1、强化学习和监督学习以及非监督学习的区别

        监督学习是使用已经标记好的数据样本，做训练来预测新的数据的类型（分类）或者值（回归）

        非监督学习是找到unlabeled 数据背后的关系

        强化学习的目标是最大化累计回报

2、如果问题不满足马尔科夫性怎么办，当前时刻的状态和它之前的很多状态有关。

        将多个时刻状态并入考虑作为一个状态，或者使用RNN来学习其中隐含的时序信息。

3、强化学习中的过拟合问题

        在某个环境中过拟合，然后在另一个环境中测试就效果不好。我们论文中表现还行：Town2训练，town5测试，效果还行。Arxiv一篇论文讲到了可能是在环境感知的部分有过拟合的问题，策略上没有问题，因此他是在前面的环境感知部分加了些正则化、dropout以及添加KL散度等防止过拟合的操作。

4、强化学习的损失函数是什么，和深度学习的损失函数有何关系？

强化学习的损失函数是累积回报，对于不同的问题设定，有着不同的形式，比如对于有限长度的MDP问题，直接用回报和作为优化目标；对于无限长的问题，需要使用折扣累积回报或者平均回报。深度学习的损失函数一般是多个独立同分布样本预测值和label之间的误差，需要最小化，而强化学习的是需要最大化。

5、简述DP、MC和TD的关系

共同点：都是用来估计值函数的方法

不同点：MC是通过采样、求均值的方法来求解；DP是基于模型的，直接计算期望，不用采样；但是仍然使用了bootstrap；TD是结合了采样和bootstrap。TD和DP相比，DP是使用模型来获得后继状态，而TD是根据实验来得到后继状态。

6、求解MDP有哪些方法，有模型用什么方法，动态规划是什么？

求解的方法有DP、MC、TD。有模型使用DP。动态规划是指，将一个复杂问题分成多个子问题，通过求解这些子问题的解，最终获得原问题的解。

7、MC、TD谁的方差大，为什么？

MC的方差大，因为MC是采样了许多条完整的episode，不同的episode之间可能差异很大；而TD使用了bootstrapping，实现了一种类似于平滑的效果，所以估计的值函数方差小。

8、RL中基于值函数的和基于PG算法的优缺点以及适用场景

        value-based是通过求解最优值函数间接去求解最优策略；而policy-based的方法是直接将策略参数化，通过策略梯度来更新策略的参数以最大化回报。

        基于值函数的方法不容易扩展到高维或者连续动作空间（难以建立Q表）；而且无法解决随机策略的问题，value-based的方法对动作值的估计最终会收敛到对应的true value，会变成一个确定的策略。

        policy-based方法在高维和连续动作空间更加有效，可以学习随机的策略，但同样地容易收敛到局部最小值、方差较大。

9、有模型RL算法和无模型RL算法的区别

有模型：环境的所有信息（转移概率和价值函数都已知了），可以使用DP来进行策略求解。

无模型：不知道状态转移概率矩阵，需要用采样来估计模型动态性，采样复杂度高，对超参数敏感，一般基于MC或者TD方法求解策略。

10、确定性策略和随机性策略

确定性策略π(s)将状态空间s映射到动作空间a，本身没有随机性质，因此，通常会结合ε-greedy或者往动作值中加入高斯噪声的方法（DDPG）来增加策略的随机性。

随机性策略π(a|s)是在条件为S的情况下，动作a的条件概率分布，本身带有随机性，获取动作时，只需要对概率分布进行采样即可。

从熵的角度来说，确定性策略的熵为0，没有任何的随机性。随机策略有利于我们进行适度的探索，确定性策略的探索问题更加严峻。

ε-greedy：以ε的概率随机选择随机动作（exploration），以1-ε的概率按照确定性策略选择动作。

11、RL中on-policy以及off-policy策略的区别，以及有哪些off-policy的方式

        on-policy是行为策略与要优化的策略是一个策略，更新了策略后，就用该策略的最新版本采样数据。

        off-policy是使用任意一个策略采集数据，利用收集的数据去更新目标策略。

on-policy利用已知当前最优选择，速度快，但是可能学不到最优解，陷入局部最优，而加入探索又降低了学习效率。样本利用率低，每次更新都需要进行新的采样。

off-policy先产生某概率分布下的大量行为数据，意在探索，从这些偏离最优策略的数据中寻找target policy，前提条件是假設π是目标策略, µ是行为策略，那么从µ学到π的条件是：π(a|s) > 0 必然有 µ(a|s) > 0成立。off-policy的缺点是曲折、收敛慢，但优势是更加强大和通用，确保了数据全面性，可重复利用数据进行训练（replay buffer）。

12、为什么有时候off-policy需要与重要性采样结合使用？

    off-policy方法中不一定非要使用重要性采样，要根据实际情况使用，比如，需要精确估计值函数时，需要采用重要性采样；若是用于是值函数靠近最优值函数则不一定。

13、重要性采样的作用？

        重要性采样一般用于off-policy，又称为off-policy correction。off-policy一般有两个策略：行为策略b和目标策略π，当我们要评估基于π的值函数Vπ和Qπ时，需要使用到历史交互样本，但是这些样本都是用策略b得到的，所以得到的结果存在偏差，需要修正。

        重要性采样则把基于行为策略b估计得到的值矫正到基于目标策略π所估计得到的值，得到基于目标策略π的无偏估计，并使得行为策略向目标策略靠拢。

重要性采样系数：

        当重要性采样系数为1时，即两个策略在状态St时选择At的概率一致，不需要矫正。                        当小于1时，说明行为策略b在状态St时选择At的概率要比目标策略π大，那么这个系数就会降低基于行为策略b得到的TD target，从而引导agent后续降低行为策略b在状态St时选择At的概率。          同理，大于1时，与之相似。

14、为什么Q-learning算法（或者DQN）作为off-policy可以不用重要性采样？

        在选择动作的时候，使用的是目标策略π，而不是行为策略b，因此不需要使用重要性采样来矫正估计值。

Q-learning的思想是从任意初始化的Q函数出发，以最优贝尔曼方程为标准去调整Q函数：

在第n轮更新时的更新式：

        

     因为最优贝尔曼方程的右侧的期望只与状态转移分布有关，而与策略无关，无论训练数据（S, A, R, S’）来自哪个策略，按照Q-learning的更新都能使Q函数接近Q*(S,A)。

15、Sarsa算法像是在进行值函数估计，为什么能够收敛到最优策略？

更新式中有1-ε的概率是按照argmax Q(S, A)来选取动作，即对策略进行提升，可以发现ε-greedy策略是一种不同于条件概率分布表示的策略，只要ε较小，则自带策略提升功能。

16、sarsa和qlearning区别 哪个谨慎 为什么

Sarsa和q-learning都是TD方法，但sarsa是on-policy，其行为策略和目标策略都是ε-greedy的，整个策略的学习是保守的，而qlearning是off-policy的，其行为策略是ε-greedy的，而目标策略是greedy，它的behavior policy可以随机去探索环境，更加激进。 qlearning是离策略的，由于是值更新使用了下一个时刻的argmax_a Q，所以我们只关心哪个动作使得 Q(s_{t+1}, a) 取得最大值，而实际到底采取了哪个动作（行为策略），并不关心。这表明优化策略并没有用到行为策略的数据，所以说它是离策略（off-policy）的。

qlearning：

sarsa:

17、策略迭代和值迭代的区别？

策略迭代包含两个步骤，策略评估与策略提升。而值迭代算法是直接估计最优值函数（直接使用贝尔曼最优方程），值迭代算法是策略评估只进行一次迭代的策略迭代算法。

18、不打破数据相关性，神经网络的训练效果为什么就不好？

在神经网络中通常使用随机梯度下降法。随机的意思是我们随机选择一些样本来增量式的估计梯度，比如常用的采用batch训练。如果样本是相关的，那就意味着前后两个batch的很可能也是相关的，那么估计的梯度也会呈现出某种相关性。如果不幸的情况下，后面的梯度估计可能会抵消掉前面的梯度量。从而使得训练难以收敛。

19、DQN采用了两个关键的trick是什么？

1. 利用经验回放来训练强化学习的学习过程：对采样得到的数据进行均匀随机采样，打破了数据间的关联性。
2. 使用目标网络来缓解训练不稳定的问题：target 网络每隔固定的次数更新一次，而用于动作值函数逼近的网络是每一步都更新。使用两个网络来减少maxQ(S’,A’)与Q(S,A)之间的关联性。

DQN的loss是什么？

        MSE loss（value-based）

20、DDQN对DQN的改进？

由于DQN每次使用当前值函数Q_target最大的动作值函数来更新当前的动作值函数，max操作会导致过估计。（因为神经网络的预测会有误差，误差会累积）

为了解耦这两个过程，将动作选择和动作评估分开来，DDQN使用了两个值网络，一个网络用来执行动作选择（local network即动作选择网络Q1），另一个用来评估动作。（Q_target）

DQN:

def declare_networks(self):

    self.model = DQN(self.num_feats, self.num_actions, body=AtariBody)

    self.target_model = DQN(self.num_feats, self.num_actions, body=AtariBody)

def get_max_next_state_action(self, next_states):

    return self.target_model(next_states).max(dim=1)[1].view(-1, 1)



max_next_action = self.get_max_next_state_action(non_final_next_states)  # 使用target网络来选择当前最大值的动作。

max_next_q_values = self.target_model(non_final_next_states).gather(1, max_next_action)

# 使用target网络来计算动作值。

expected_q_values = batch_reward + (self.gamma*max_next_q_values)  # TD target

#estimate

current_q_values = self.model(batch_state).gather(1, batch_action)

diff = (expected_q_values - current_q_values)

即

cur_q = q_excepted(s, a)

td_target = r + gamma*max(q_target(s’, a’))

#   a’ = q_target(s’).max()

mse(td_target, cur_q)

DDQN：

def declare_networks(self):
    self.model = DQN(self.num_feats, self.num_actions, body=AtariBody)
    self.target_model = DQN(self.num_feats, self.num_actions, body=AtariBody)
def get_max_next_state_action(self, next_states):
    return self.model(next_states).max(dim=1)[1].view(-1, 1) 
 #选择动作的网络变成了model网络，而不再是target网络。

即：

q_excepted_val = q_excepted(s, a)
a* = argmax(q_excepted(s’))      # 用q_excepted网络来选择action
td_target = r + gamma*q_target(s’, a*)
mse(td_target, q_excepted_val)

21、有哪些方法可以使得RL训练稳定？

1. 经验池回放：打破数据间的相关性。
2. Batch normalization：使得输入数据有统一的均值和方差。
3. 使用目标网络来处理TD值。
4. 使用advantage function：一是提高学习速率，让学习更加稳定；二是有助于减少方差，方差过大会导致过拟合。
5. TRPO限制梯度更新步长，使得目标稳步提高。

22、常见的平衡探索与利用的方法

        e-greedy：如DQN、Q-learning

        添加噪声项：DDPG

        熵：PPO

        UCB：多臂老虎机

23、A2C中的advantage function 和DQN中的advantage function 有什么区别？

        即一个是policy based， 一个是value based。

        dqn中，引入advantage function是为了更好地对最优值函数Q(s, a)进行估计，帮助找到最优策略。

        AC算法中，advantage function 是针对策略π，好的策略，advantage function>0，反之小于0.从而提升当前策略。

24、Actor、Critic两者的区别是什么？

actor是决策模块，输出动作；而critic是判别器，用来计算值函数。

25、actor-critic框架中的critic起了什么作用？

critic表现了对于当前决策好坏的衡量，结合策略模块，当critic判别某个动作的选择是有益的时，策略就更新参数以增大该动作出现的几率，反之则降低动作出现的几率。

26、策略梯度中的基线（baseline）如何确定？

        基线只要不是动作a的函数就可以，常用的选择就是状态值函数v(s)，代表了在该状态s下所有动作值函数关于动作概率的平均值。

27、为什么baseline可以直接减去一个值而对策略迭代没有影响？

推导过程

因此，减去个与动作无关的baseline是不会改变策略梯度值的。

28、DDPG是on-policy还是off-policy，为什么？

off-policy，因为DDPG为了保证一定的探索，对于输出的动作加了一定的噪声，也就是说行为策略不再是优化的策略。

DDPG的主要特点：

        1、可以看做是DQN + AC + DPG的组合。

        2、Actor部分使用DPG的思想进行更新，使用critic部分的Q值对action的梯度来对actor进行更新。

        3、critic部分的输入是states和action。

        4、使用了DQN的思想，加入了replay buffer，随机抽样，目标网络，real Q值使用两个target网络共同计算。

        5、将target网络更新变为soft update，在每个batch缓慢更新target网络的参数。

        6、在输出的动作上添加了噪声。

与AC算法的区别：

1. actor和critic都有两个网络，critic_target网络中的动作来自actor_target网络，而不是通过argmax得到。
2. Actor的动作选择上，使用的是确定性策略，而不是随机策略。

DDPG的框架结构图

29、A3C是on-policy，为什么？

异步更新，不同的agent在机器上并行运行也可以看做是在探索环境的不同部分，同时也可以让不同的agent采用不同的策略，这样就可以进一步扩大化数据的多样性，也使得进行在线更新的样本之间的关联度减少。

30、DDPG与A3C的区别？

1. DDPG有4个网络，而A3C网络是共享基础层，只是输出层会分为value和policy两个分支。

        DDPG无法共享actor和critic的基础层：

                1、actor的输入是state，而critic的输入是（state，action）

                2、关于梯度问题，一般只使用critic的梯度更新共享层，因为对于DDPG来说，Q函数基本收敛了，policy才能基本收敛。

      2、A3C是通过多个agent在多个环境实例中异步执行和学习，不同线程使用不同的探索策略，使得数据关联性很小，而DDPG是通过经验池来降低关联性。

     3、A3C是随机策略，DDPG是确定性策略。

     4、DDPG的actor部分是使用DPG的思想进行更新，使用critic部分Q值对action的梯度来对actor进行更新。而A3C是通过PG思想来进行更新。

      5、A3C没有target network。

31、GAE中两个参数哪个控制偏差，哪个控制方差？

        GAE是对n-steps TD估计advantage值的优化，将不同n值的TD估计以衰减的方式糅合在一起。相当于是介于“回合更新”与“单步更新”之间的“多步更新”算法。

λ用于在bias与variance之间寻找平衡，λ小，方差变小，偏差变大；λ大，方差变大，偏差变小；

for t in range(num_step - 1, -1, -1):
    delta = rewards[t, :] + gamma * values[t + 1, :]*(1-dones[t, :]) - values[t, :]
    gae = delta + gamma * lam * (1 - dones[t, :]) * gae

32、TRPO、PPO都是on-policy的

        在整个训练的宏观视角下，PPO仅学习当前策略产生的样本，学完之后就丢弃。在微观视角下，PPO对当前策略产生的样本进行多轮学习，充分挖掘样本学习潜能，提高样本利用率，并加入clip保证策略提升稳定。

        所以，PPO是从on-policy出发，放宽了对目标策略和行为策略的严格约束，提高了on-policy的样本利用率，并加入clip来保证策略是可以稳定提升的。

35、Advantage大于0或者小于0时，clip是怎么操作的？

A3C（Asynchronous Advantage Actor-Critic）

A3C是在A2C的基础上，基于利用“平行宇宙”的概念，模拟不同的环境，用不同的环境进行A2C，然后集中云化更新参数。其实就是利用云化，分布式计算的思想。

步骤是：1.复制全局参数 2.采样抽取数据 3.计算梯度数据 4.更新全局参数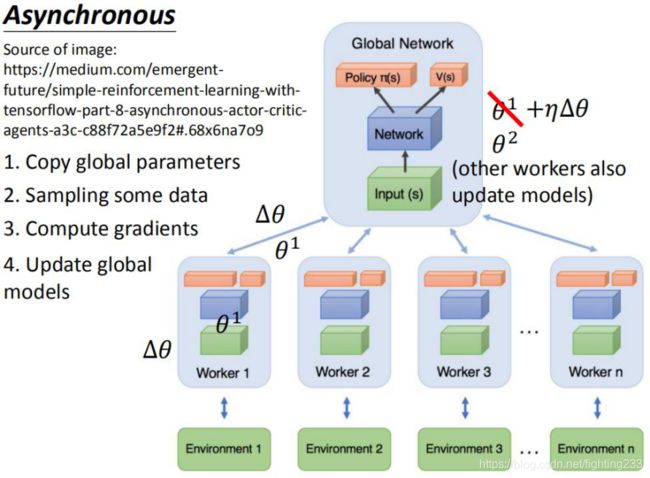    

利用多线程，同时在多个线程里面分别与环境进行交互学习，每个线程将学习的成果进行汇总，整理保存在一个公共空间，定期从公共空间将成果拿出来，知道学习交互。通过这种方法，避免了经验回放相关性过强的问题，做到了异步并发。

图中的global network即为公共部分，是一个公共的神经网络模型，包括actor和critic两个部分。下面有n个worker线程，每个线程里有和公共的神经网络一样的网络结构，每个线程会独立地和环境进行交互得到经验数据，这些线程之间互不干扰，独立运行。

每个线程和环境交互到一定数量的数据后，就计算在自己线程里的损失函数的梯度，但是这些梯度不更新自己线程里的神经网络，而是去更新公共的神经网络，

https://github.com/ikostrikov/pytorch-a3c/blob/master/main.py

如何应对不收敛的问题，加快收敛？

1. 可以使用专家数据学习一个baseline，在这个基础上进行强化学习；
2. 从建模上入手，在设计MDP时，降低问题难度，减少动作空间等；
3. 并行化，引入更多资源。

多臂赌博机

“探索与利用”的问题

1、Greedy方法与Ɛ-greedy方法；

2、动作价值的初始化可以作为鼓励agent探索的方式之一，optimistic initial values就是指在动作价值初始化的时候设置为一个正数，是乐观的，鼓励agent去多探索

3、UCB（upper-confidence-bound action selection）

Ɛ-greedy方法是强迫以一定的概率去探索，但是缺点是对动作不加区别，以等概率去探索所有动作，一个更有效的方式是根据动作的潜力去选择动作，同时考虑估计值的大小与估计值的不确定性来定义潜力：

Nt(a)表示在t时刻之前动作a被选择的次数，c控制探索的长度，置信上界选择的核心思想是用平方根项来衡量对动作a价值估计的不确定性。而使用自然对数的原因是让不确定性的变化趋势随着时间的增加而减小。所有的动作最终都能被选到，但是对于估值低的动作或者被频繁选择的动作， 会降低其选择的概率。

4、Thompson sampling算法

假设每个臂能产生收益的概率为p，并且p的概率分布符合beta(wins, lose)； 每个臂都维护其beta分布的参数，每次试验后，选中一个臂摇一下，有收益的话wins+1，否则，lose+1；

每次选择臂的方式是，通过用每个臂现有的beta分布产生一个随机数，选择所有臂中随机数最大的臂去摇。

np.argmax(pymc.rbeta(1 + successes , 1 + totals - successes))