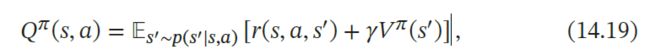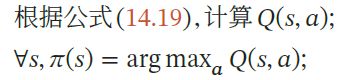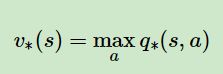强化学习动态规划之策略迭代&价值迭代

在强化学习中，当环境模型已知时（也即环境状态转移概率和奖励已知），可以采用动态规划的思想来解决强化学习问题，常用的有策略迭代算法和值迭代算法两种，以下展开具体介绍。

1.动态规划与强化学习的联系

动态规划相信大家都不陌生，很多算法都会使用到它。动态规划（Dynamic Programming,DP）是一种将复杂问题简单化的思想，而不是指某种具体的算法。DP算法通过把复杂问题分解为子问题，通过求解子问题进而得到整个问题的解。在解决子问题的时候，其结果通常需要存储起来被用来解决后续复杂问题。一个复杂问题可以使用DP思想来求解，只要满足两个性质就可以：(1)一个复杂问题的最优解由数个小问题的最优解构成，可以通过寻找子问题的最优解来得到复杂问题的最优解；(2)子问题在复杂问题内重复出现，使得子问题的解可以被存储起来重复利用。巧了，强化学习要解决的问题刚好满足这两个条件。还记得贝尔曼方程吗？如下：

不难发现，当模型已知时（即公式中的a,P,R都已知），我们可以定义出子问题求解每个状态的状态价值函数，同时这个式子又是一个递推的式子, 意味着利用它，我们可以使用上一个迭代周期内的状态价值来计算更新当前迭代周期某状态s的状态价值。可见，使用动态规划来求解强化学习问题是比较自然的。

注意一下符号的含义：

上图转自：https://zhuanlan.zhihu.com/p/86525700 

2.策略迭代方法

知道了动态规划与强化学习的联系，我们就能用DP的思想去求解强化学习问题。策略迭代包括策略评估(Policy Evaluation)和策略改进(Policy Improvement)，其基本过程是从一个初始化的策略出发，先进行策略评估，然后策略改进，评估改进的策略，再进一步改进策略，经过不断迭代更新，直到策略收敛。下面具体介绍策略评估和策略改进。

2.1 策略评估

有些公式不好打，直接贴出别人的解释：

上图转自：https://www.cnblogs.com/pinard/p/9463815.html

具体求解实例如下：

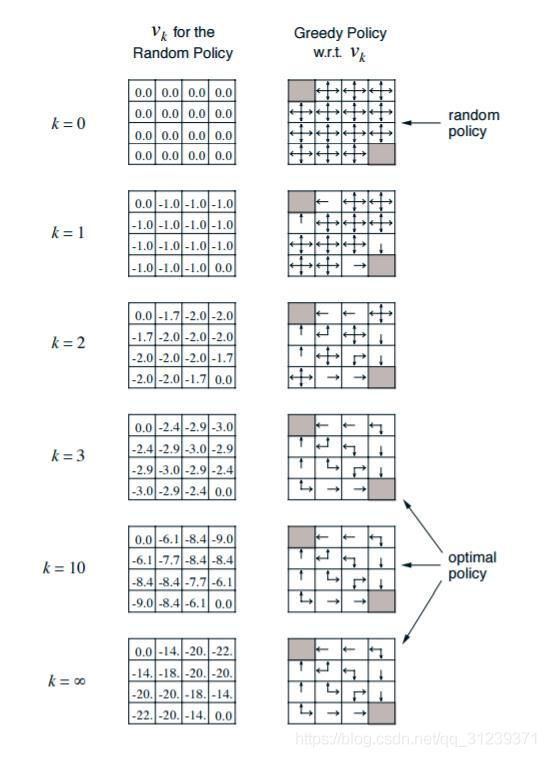
上面是一个经典的Grid World的例子。我们有一个4x4的16宫格。左上和右下的格子是终止格子，它们的价值固定为0，个体如果走到这两个位置，则停止移动，且之后每轮的奖励都是0。个体在其他格子的每次移动，得到的瞬时奖励都是-1。个体每次只能移动一个格子，且只能上下左右4种移动选择，不能斜着走。如果在边界格往外走，则会直接移动回到之前的边界格。衰减因子定义为γ=1。由于这里每次移动，下一格都是固定的，因此所有可行的的状态转化概率P=1。这里给定的初始策略是随机策略，即每个格子里有25%的概率向周围的4个格子移动。

首先将所有格子的状态初始化为0，即图中k=0时的情况（策略评估部分关注的是上图中左侧的表格，即各个状态的价值函数）。由于终止格子的价值固定为0，我们可以不将其加入迭代过程。下面以第三行第一个格子为例，给出不同迭代轮次的计算过程：

就这样一直迭代下去，直到每个格子的策略价值改变很小为止。这时我们就得到了所有格子的基于随机策略的状态价值。 

2.2策略改进

此时在已知每个格子的状态价值后，就可以利用动态规划的思想来解决接下来的策略改进问题。一种可行的方法就是根据我们之前基于任意一个给定策略评估得到的状态价值来及时调整我们的动作策略，调整的方法就是贪婪法。具体来说就是：个体在某个状态下选择的行为是其能够到达后续所有可能的状态中状态价值最大的那个状态。以2.1小节中的内容为例，图右面为策略的选择。当k=无穷大（即状态值收敛）时，第三行第一列的格子周围的状态值分别是-14，-20，-20，那么按贪婪法，我们应该调整动作，往-14的那个方向移动，也即图中的箭头向上。按此规律，就可以得到其他格子的策略，此时一轮策略迭代结束。

解释：这里策略改进的依据其实是找出令Q函数最大的那个动作，即：

 因为在Grid World的例子中，所有可行的的状态转化概率P=1，瞬时奖励都是-1，衰减因子定义为γ=1，所以其实Q函数的值就是下一个状态的状态值，这也就是为什么直接往状态价值最大的那个状态移动就可以的原因。

因此，总结一下，策略迭代就是在循环进行两部分工作，第一步是使用当前策略π∗评估计算当前策略的最终状态价值v∗，第二步是根据状态价值v∗根据一定的方法（比如贪婪法）更新策略π∗，接着回到第一步，一直迭代下去，最终得到收敛的策略π∗和状态价值v∗。

3.价值迭代方法

策略迭代算法中的策略评估和策略改进是交替轮流进行，其中策略评估也是通过一个内部迭代来进行计算，其计算量比较大．事实上，我们不需要每次计算出每次策略对应的精确的值函数，也就是说内部迭代不需要执行到完全收敛。

值迭代整体思路：由于最优策略对应最优值函数，因此可以通过直接求出最优值函数，就能推出最优策略。所以这个思路的核心就是怎么把最优值函数求出来。

最优值函数求解的关键就是贝尔曼最优方程，如下：

所以就可以通过递推的形式去求最优值函数。贝尔曼最优方程具体解析可以参考：

https://www.cnblogs.com/pinard/p/9426283.html

https://zhuanlan.zhihu.com/p/54728513

求得最优值函数，根据下式就可以去选择最优策略下的动作了：

值迭代的整体流程如下：

 上图来自：复旦大学计算机科学技术学院教授邱锡鹏老师的《神经网络与深度学习》一书

 

参考资料：

https://www.cnblogs.com/pinard/p/9463815.html

https://smiler666.github.io/post/rl-policy-iteration/

https://www.zybuluo.com/Team/note/1125995

https://www.pianshen.com/article/7959987079/

https://zhuanlan.zhihu.com/p/360029207

https://zhuanlan.zhihu.com/p/33229439