第四章 MATLAB的数学运算

4.1 多项式与插值

数学运算时MATLAB的核心，其他领域的应用都以这些数学运算为基础，如矩阵运算、代数运算、解方程等等。MATLAB的强大之处正是在于其对几乎所有数学问题的解决方案。本章将介绍MATLAB的部分基础数学功能，包括多项式，线性插值，傅里叶变换和微分方程等。这些数学知识在今后的学习中会经常用到，非常重要。

4.1.1 多项式的表示

多项式在数学中有着极为重要的作用，而多项式的运算也是工程和应用中经常会遇到的问题。
在MATLAB中多项式用一个行向量表示，向量中的元素为该多项式的系数，按照降序排列。例如，多项式$4x^3+3x^2+6x^1+9$可以表示为向量$P=[4,3,6,9]$。用户可以用创建向量的方式创建多项式，再利用poly2sym函数将其显示为多项式。

例子：

clear all; clc;

P = [4, 3, 6, 9];
% 默认变量为x
y = poly2sym(P)

4.1.2 多项式的四则运算

使用向量来表示多项式使得多项式的四则运算变得简单，因为可以直接转换为向量的运算。
多项式的加减即为对应系数项的加减，因此可以通过向量的加减来完成。进行加减运算的两个向量需要有相同的长度，因此对低阶多项式需要补零
多项式的乘法和除法实际上是多项式系数之间的卷积和反卷积运算。MATLAB有相应的卷积函数conv和deconv。
例子：

clear all; clc;
% polynomial operation
p1=[1 2 1];                         		%定义多项式
p2=[1 1];
length_of_p1=length(p1);
length_of_p2=length(p2);
if length_of_p1 == length_of_p2     		%判断两个多项式的长度是否相等
    p1_plus_p2 =p1+p2;              		%多项式相加
    p1_minus_p2=p1-p2;              	%多项式相减
elseif length_of_p1 < length_of_p2
        temp_p1=[zeros(length_of_p2-length_of_p1) p1];
        p1_plus_p2 =temp_p1+p2;
        p1_minus_p2=temp_p1-p2;
else
    temp_p2=[zeros(length_of_p1-length_of_p2) p2];
    p1_plus_p2 =p1+temp_p2;
    p1_minus_p2=p1-temp_p2;
end
p1_multiply_p2=conv(p1,p2);         		%多项式相乘
p1_divide_p2  =deconv(p1,p2);       		%多项式除法
p1=poly2sym(p1)                    		%显示多项式 p1
p2=poly2sym(p2)                    		%显示多项式 p2
p1_plus_p2 =poly2sym(p1_plus_p2)
p1_minus_p2=poly2sym(p1_minus_p2)
p1_multiply_p2=poly2sym(p1_multiply_p2)
p1_divide_p2  =poly2sym(p1_divide_p2)

4.1.3 多项式的其他运算

表4-1 多项式运算函数

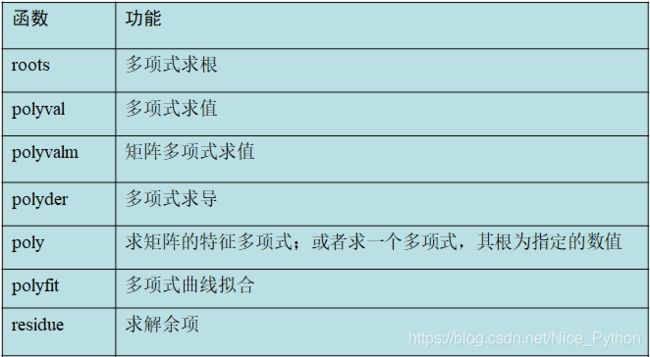
这些都是多项式运算中常见的函数。下面分别简要举例介绍一下。
roots() 和 poly()

clear all; clc;
% roots求多项式的根--注意与root的区别
A = [1 2 1];
yA = poly2sym(A)
a = roots(A)

%%
B = [1, 4, 5, 3, 6, 7];
yB = poly2sym(B)
b = roots(B)

%% 
% poly求具有特定根的多项式
A2 = poly(a)

B2 = poly(b)

%%
% poly求矩阵的特征多项式
P = magic(4);
p = poly(P);
y = poly2sym(p)
x = roots(p)

polyvar多项式求值

clear all; clc;

% 求多项式的值
p = [4 3 2 1];
polyval(p, 4)

x = roots(p)
polyval(p, x)

%%
% 尝试用另一种方法？
syms x
y = poly2sym(p);
disp(y)
r = root(y, x);
vr = vpa(r);
disp(vr)
n = polyval(p, double(vr))

polyder多项式求导

clear all; clc;

a = [1, 2, 1];
% x^2 + 2x + 1
ya = poly2sym(a)

b = [1, -1];
% x-1
yb = poly2sym(b)

% da
p1 = polyder(a);
dya = poly2sym(p1)

% d(ab)
p2 = polyder(a,b);
dy2 = poly2sym(p2)

% d(a/b)
[q, d] = polyder(a, b);
dy3 = poly2sym(q) / poly2sym(d)

polyfit多项式拟合
曲线拟合是工程中经常要用到的技术之一。MATLAB提供了曲线拟合工具箱和多项式拟合函数。函数polyfit给出了使用最小二乘法拟合的多项式。函数调用格式为p = polyfit(x, y, n)，其中x, y分别为要拟合数据的坐标，应该是相同长度的向量，n则是用于拟合的多项式的次数。

clear all; clc;
x = 0 : pi/10 : 2*pi;
y = sin(x);

z = polyfit(x, y, 3);

% 画图
plot(x, y, 'r*')
hold on
f = poly2sym(z);
ezplot(f, [0, 2*pi])

4.1.4 数据插值

另一种工程上常见的问题是数据插值，即根据已知数据推断未知数据。
插值运算时根据已有数据的分布规律，找到一个可以连接起已知各点的函数表达式，并用这一函数表达式来预测处于已有数据两点之间任意位置的数据。
MATLAB提供了对数组的任意一维数据进行插值的工具，这些工具大多需要用到多维数组的操作。本节主要介绍对一维数据插值。
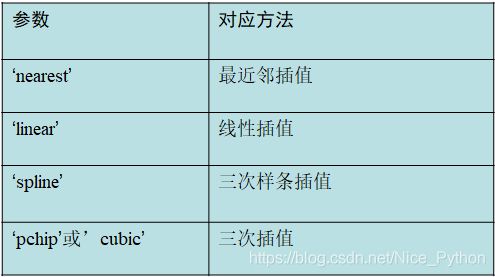
一维数据插值在曲线拟合和数据分析中具有重要的地位。在MATLAB中，一维数据插值主要由函数interp1来实现（即interpolation1的缩写）。该函数的调用格式为yi = interp1(x, y, xi, method)，其中x,y 为所采用的数据的坐标，均是一维向量；xi为待插值的位置，method为采用的插值方法，返回插值结果。而该函数有四种method，不同method得到的结果会有些许差异。

表4-2 插值函数中可选的方法

例子：

% Interpolation using the four methods
x=[0 3 5 7 9 11 12 13 14 15];
y=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.4 1.6];
length_of_x=length(x);
scalar_x=[x(1):0.5:x(length_of_x)];
length_of_sx=length(scalar_x);
for i=1:length_of_sx
    y_nearest(i)=interp1(x,y,scalar_x(i),'nearest');
    y_linear(i) =interp1(x,y,scalar_x(i),'linear');
    y_spline(i) =interp1(x,y,scalar_x(i),'spline');
    y_cubic(i) =interp1(x,y,scalar_x(i),'pchip');
end
subplot(2,2,1),plot(x,y,'*'),hold on,plot(scalar_x,y_nearest),title('method=nearest');
subplot(2,2,2),plot(x,y,'*'),hold on,plot(scalar_x,y_linear),title('method=linear');
subplot(2,2,3),plot(x,y,'*'),hold on,plot(scalar_x,y_spline),title('method=spline');
subplot(2,2,4),plot(x,y,'*'),hold on,plot(scalar_x,y_cubic),title('method= pchip ');

$\ast$最近邻插值将插值点xi的值设置为举例最近的点的对应值。
$\ast$线性插值用分段线性函数拟合已有数据，返回拟合函数在xi处的值。
$\ast$三次样条插值采用样条函数对数据拟合，并且任意两点之间的函数为三次函数。
$\ast$三次插值为一组方法，通过pchip函数对数据进行三次Hermite插值，这种方法可以保持数据的一致性和数据曲线形状。

可以看出，最近邻插值效果最差，其他三种方法差别不是很大，实际上三次插值的效果相对较好，但是运行效率更差。在实际应用中，需要根据实际情况综合考虑来选取合适的插值方法。

傅里叶插值法

MATLAB针对一维数据还有另一种方法，基于傅里叶变换的方法。这种方法将输入数据视为周期函数的采样数据，对数据进行傅里叶变换，然后对更多的点进行傅里叶变换。函数名为interpft（interpolation fourier transform），调用方式为y = interpft(x, n)，其中x为周期函数的均匀采样数据，n为待返回的数据个数。当我们对周期数据或近似周期数据进行插值时，该方法更加合适。

例子：

clear all;clc;

x = 0:pi/5:2*pi; % 10个数据
y = sin(x);
plot(x, y);

hold on
y1 = interpft(y, 20);

x1 = linspace(0, 2*pi, 20);
plot(x1, y1, '.')

可以看出，interpft的插值效果令人满意。尤其是当我们增加数据量之后。==需要注意的是函数的输入参数n表示对输入的采样值x重新插值后返回的数据长度，因此n要大于输入的x的长度。返回的n表示在原始数据的相同采样时间内的等间距的采样数据。

外插运算

若要获得已知的数据集外的插值数据，则需要用到外插，这是比较困难的，且精度不高。MATLAB中可以通过对
interp1函数添加’extrap’参数来指明所用的插值算法，并表示需要外插运算。另一种方法是将数据集外的函数点赋值为extraval，可以赋值为Nan或者0。

例子：

clear all; clc;

x=0:0.5:10;
y=cos(x);
x1 = linspace(0,2*pi,20);
y1=cos(x1);
y2=interp1(x,y,x1,'nearest')           %没有指定外插算法，估值都返回NaN
y2=interp1(x,y,x1,'nearest','extrap')  %指明插值算法也用于外插运算
y3=interp1(x,y,x1,'linear','extrap');
y4=interp1(x,y,x1,'spline','extrap');
y5=interp1(x,y,x1,'pchip ','extrap');
plot(x,y,x1,y1,'o',x1,y2,'-',x1,y3,'-.',x1,y4,'--',x1,y5,'*')

4.2 函数运算

函数是数学中的一个重要概念。这一节我们学习MATLAB的一些基础的函数功能。

4.2.1 函数的表示

MATLAB提供了两种表示函数的方法：一种是利用m文件将函数定义为MATLAB函数；另一种是采用匿名函数。
例子：建立函数$f(x)=\frac{1}{(x-0.3{)}^2+0.01}+\frac{1}{(x-0.9{)}^2+0.04}-6$
方法一：建立m文件。这是MATLAB的内置函数humps()，找到humps.m文件，打开内容如下。

function [out1,out2] = humps(x)
%HUMPS  A function used by QUADDEMO, ZERODEMO and FPLOTDEMO.
%   Y = HUMPS(X) is a function with strong maxima near x = .3
%   and x = .9.
%
%   [X,Y] = HUMPS(X) also returns X.  With no input arguments,
%   HUMPS uses X = 0:.05:1.
%
%   Example:
%      plot(humps)
%
%   See QUADDEMO, ZERODEMO and FPLOTDEMO.

%   Copyright 1984-2014 The MathWorks, Inc.

if nargin==0
   x = 0:.05:1;
end

y = 1 ./ ((x-.3).^2 + .01) + 1 ./ ((x-.9).^2 + .04) - 6;

if nargout==2,
   out1 = x;
   out2 = y;
else
   out1 = y;
end

那我们想要调用该函数，可以通过符号"@"获取函数，如：

fh = @humps;  % 将fh定义为humps函数
fh(1.5)

%%
% 当然也可以直接用humps
humps(1.5)

方法二：匿名函数，例如：

clear all; clc;

fh = @(x) 1 ./ ((x - 0.3).^2 + 0.01) + 1 ./ ((x - 0.9).^2 + 0.04) -6;
fh(1.5)

==**需要注意的是，尽管这两种方法都得到了函数的解。但是，我们仔细阅读humps.m文件内容会发现，该函数不只有一种返回值。若我们使用[x, y] = humps(a) 的形式来调用该函数，该函数不仅会返回函数值y， 还会返回变量值x。而使用匿名函数则无法实现该功能。当然，匿名函数比写脚本要更简单。因此，在实际项目中，可以根据需要确定建立函数的方法。

4.2.2 绘制数学图像

函数图像让我们能够直观的查看函数的总体特征。MATLAB提供了绘制函数图的函数fplot。我们在文档中查看一下fplot函数的使用方法。

help flot

>>fplot - 绘制表达式或函数

    此 MATLAB 函数 在默认区间 [-5 5]（对于 x）绘制由函数 y = f(x) 定义的曲线。

    fplot(f)
    fplot(f,xinterval)
    fplot(funx,funy)
    fplot(funx,funy,tinterval)
    fplot(___,LineSpec)
    fplot(___,Name,Value)
    fplot(ax,___)
    fp = fplot(___)
    [x,y] = fplot(___)

    另请参阅 fcontour, fmesh, fplot3, fsurf, hold, title, Function Line 属性, 
        Parameterized Function Line 属性

    fplot 的参考页

以后我们会经常使用help文档来查看MATLAB内置函数的使用方法。实际上MATLAB的帮助文档是学习MATLAB的最好教材，同学们要学会利用，经常查阅。
通过帮助文档学习fplot的用法。

例子：绘制humps函数图像

fh = @humps;

subplot(1, 2, 1), fplot(fh);
subplot(1, 2, 2), fplot(fh, [-3, 3]);

4.2.3 求函数的极值

本章介绍MATLAB求一元函数和二元函数的极值和曲线拟合方法。

求一员函数极小值

fminbnd()函数

% 求humps函数在（0.3， 1）的极小值坐标
f = @humps;
x = fminbnd(f, 0.3, 1)

f(x)

help fminbnd 给出具体用法

clear all; clc;
function f = scalarobjective(x)
f = 0;
for k = -10:10
    f = f + (k+1)^2*cos(k*x)*exp(-k^2/2);
end

%%
x = fminbnd(@scalarobjective,1,3)

%%
options = optimset('Display', 'iter');
x = fminbnd(@scalarobjective,1,3, options)

%%
[x, fval, exitflag, output] = fminbnd(@scalarobjective,1,3, options)

最基本的用法一般满足绝大部分需求，特殊情况需要自己设置参数。

多元函数求极值

本函数为fminsearch()。该函数内部使用Nelder-Mead单一搜索算法，通过调整各个元素的值来寻找f(x)的极小值，适用于不太平滑、难以计算梯度信息或者梯度信息价值不大的函数。
以Rosenbrock函数为例

%创建函数
function f = banana(x)
f = 100*(x(2) - x(1)^2)^2 + (1 - x(1))^2;
end

% 函数图像
hf = @(x,y) 100*(y-x.^2).^2+(1-x).^2
ezmesh(hf, [-1,1])

% 搜索最小值
hf = @banana;
[x, fvalue,flag,output] = fminsearch(hf, [-2, 2])

4.2.4 函数求解

fzero()求解一元函数的零点。需要制定一个初始点或者指定一个区间。 help fzero查看用法。注意！该函数是通过查找变号的位置来作为零点，因此不能求解例如x^2的根。 例子

% 求解f(x)=logx+sinx-2在x=6附件的解。
f = @(x) log(x) + sin(x) - 2;
[x, y, exitflag, output] = fzero(f, 6)

%%
%通过函数图像查看。
fplot(f, [x-2, x+2]);
hold on
plot(x, y, 'k*')

另一个求根的方法,roots函数求解多项式的根，仅限多项式。上一节的内容。

4.2.5 数值积分

一元函数的积分

两个方法quad和quadl，区别在于算法，前者使用自适应递归Simpson方法，后者采用高阶的自适应Lobatto方法。

例子：
[q, fcnt] = quad(fun, a, b, tol, trace);
q积分值；fcnt迭代次数；fun函数；[a,b]积分区间；tol误差；trace迭代过程；

f =@(x) sin(x);
[q, fcnt] = quad(f, 0, pi, 1e-6, 1)

一元函数的矢量积分

矢量积分相当于多个一元函数积分。当被积函数中含有参数，需要对该参数的不同值计算同一个函数的积分时，可以使用矢量积分。`

clear all;clc;
f = @(x, sigma) exp(-x^2./(2.*(1:sigma)))./sqrt(2*pi .* (1:sigma));
quadv(@(x)f(x, 3), 0, 2)

更好的解法：

q = integral(@(x)f(x, 3), 0, 2, 'ArrayValued', true)

integral 函数表示普通的数值积分，采用全局自适应积分。
用法：help integral`

二重积分和三重积分

在MATLAB中二重积分和三重积分分别使用函数dblquad和函数triplequad实现。
q = dblquad(fun, xmin, xmax, ymin, ymax)；用法类似

f = @(x, y) y*sin(x) + x*cos(y);
q = dblquad(f, pi. 2*pi, 0, pi)

含参函数

在MATLAB中，对于含参函数也可以使用嵌套函数和匿名函数的方法，两者有些微差别。

嵌套函数

该方法通过m文件函数，以函数参数为输入，在函数参数内调用函数的函数来处理含参函数。见例子：

% 寻找函数f(x)=x^3+a*x^2+b*x+c的极值
function [x0, y] = funmin(a, b, c,x1,x2)
options = optimset('Display','off');
[x0, y] = fminbnd(@poly3, x1, x2, options);
    function y = poly3(x)  % 内置函数
        y = x^3 + a*x^2 + b*x + c;
    end

% 画图
fplot(@poly3, [x1, x2]);
hold on;
plot(x0, y, '.');
end

匿名函数

使用匿名函数同样可以实现这个函数，见例子：

1. 创建一个含参数的函数，保存为m文件。输入为自变量和所有的参数。

% 含参函数主体
function y = poly3_fun(x, a, b, c)

2. 在调用函数的函数前对参数赋值。
3. 用含参函数创建匿名函数。
4. 把匿名函数的句柄传递给函数的函数进行计算。

function [x0, y] = funmin_para(a, b, c, x1, x2)
options = optimset('Display','off');
[x0, y] = fminbnd(@(x)poly3_fun(x, a, b, c), x1, x2, options);

% 画图
fplot(@(x)poly3_fun(x, a, b, c), [x1, x2])
hold on
plot(x0, y, '.')
end

多元函数与一元函数类似。

4.3 微分方程

MATLAB能够求解的微分方程包括常微分方程初值问题、常微分方程的边值问题、时滞微分方程初值问题及偏微分方程问题。这里重点介绍前两个。另外MATLAB提供了偏微分方程工具箱，用于求解偏微分方程问题。

常微分方程的初值问题

MATLAB可以直接求解的常微分方程包括下面三种类型。
1. 显式常微分方程，y’=f(t,y)。
2.线性隐式常微分方程，M(t,y)y’=f(t,y)，其中M(t,y)为矩阵。
3.全隐式常微分方程f(t, y, y’) = 0。

显示常微分方程

函数命令：[t, y] = solver(odefun, tspan, y0, options) 输入参数：odefun——待求解的方程 tspan——积分区间 y0——初值，向量 options——指定求解算法。 对于非刚性方程一般用龙格库塔即ode45或ode23，还可以使用ode113---Adams-Bashforth-Moulton算法，该算法对精密步长及方程难以估计时的情况效果更好。 对于刚性方程可以用ode15s，首选，然后ode23s采用二阶改进Rosenbrock算法。还有一种算法为ode23t，采用自由内插的梯形规则。最后还有一种选项为ode23tb。

例子：求解范德蒙方程$y^{\prime \prime }-u(1-y^2)y^{\prime }+y=0$，其中u=1。
解：记$z=y^{\prime }$，则上述方程可以改写为：

$z^{\prime }=(1-y^2)\ast z-y$

1. 创建函数，用于表示该方程

function dydt = vdp1(t, y)
dydt = [y(2); (1- y(1)^2)*y(2) - y(1)];
end

2. 求解该函数

[t, y] = ode45(@vdp1, [0, 20], [2; 0]);

% 画图
plot(t, y(:, 1), '-', t, y(:, 2), '--');
title("范德蒙方程的解，u=1");
xlabel('time t');
ylabel('solution y');
legend('y', 'z');

例子2：求解u=1000时范德蒙方程的解.
当u=1000时，范德蒙方程为刚性问题，采用ode15s求解。

1. 改写函数为vdp1000

function dydt = vdp1000(t, y)
dydt = [y(2); 1000 * (1- y(1)^2)*y(2) - y(1)];
end

2. 调用ode15s求解

[t, y] = ode15s(@vdp1000, [0, 3000], [2; 0]);

% 画图
plot(t, y(:, 1), '-');
title("范德蒙方程的解，u=1000");
xlabel('time t');
ylabel('solution y');
figure
plot( t, y(:, 2), '--');
title("范德蒙方程的解，u=1000");
xlabel('time t');
ylabel("solution y'");

尝试一下使用不合适的求解器求解会出现什么呢？

完全隐式常微分方程

完全隐式常微分方程的形式为: f(t, y, y’) = 0。 即原函数和函数的导数是耦合在一起的。MATLAB中的函数ode15i用来求解这一类方程。
用法为：[t, y] = ode15i(odefun, tspan, y0, yp0, options)，输入参数与之前的类似，其中y0和yp0指初值，需要满足f(t, y0, y0’) = 0。

例子：求解$$t{y}^2(y^{\prime }{)}^3-y^3(y^{\prime }{)}^2+t(t^2+1)y^{\prime }-t^{2}y=0$$，初值为$$y(1)=\sqrt{3/2}$$
解：

1. 建立函数

function dydt = pp(t, y, yp)
dydt = t*y^2*yp^3 - y^3*yp^2 + t*(t^2 + 1)*yp - t^2*y;
end

2. 在解微分方程前，需要先求出y’(1)的初值。

t0 = 1;
y0 = sqrt(3/2);
yp0 = 0;
[y0, yp0] = decic(@pp, t0, y0, 1, yp0, 0);
yp0

3. 使用ode15i求解

[t, y] = ode15i(@pp, [1, 10], y0, yp0);

% 与解析解比较
yt = sqrt(t.^2 + 0.5);
plot(t, y, t, yt, 'o')

常微分方程的边值问题

bvp4c 函数用于求解常微分方程边值问题，该函数调用方式如下。
sol = bvp4c(odefun, bcfun, solinit, options)；其中odefun为待求函数, bcfun为边界条件, solinit为一个结构体，是该方程解的一个估计值。options 也是一个结构体，可以通过函数bvpset创建。
结构体是MATLAB的一个新的数据类型，具体怎样，下一章再讲。

例子： 求解方程 $$y^{\prime \prime }+|y|=0$$, 边值条件为 y(0) = 0和y(t) = -2。

解：

1. 将方程改写为一阶微分方程：
   $$y{1}^{\prime }=y2;y{2}^{\prime }=-|y|$$
2. 创建函数和边值条件

% 函数体
function dydx = eqode(x,y)
  dydx = [y(2), - abs(y(1))];
end

% 边值条件
function res = eqbc(ya,yb)
  res = [ ya(1), yb(1) + 2];
end

3. 创建solinit估计值，并求解

% 创建估计值
solinit = bvpinit(linspace(0, 4, 5), [1, 0]);

% 求解
sol = bvp4c(@eqode, @eqbc, solinit);

% 画图显示
x = linspace(0, 4);
y = deval(sol, x);
plot(x, y(1, : ))

4.4 习题

1. 有如下数据：

变量	值
x	1	1.1	1.2	1.3	1.4
y	1.0	1.23368	1.55271	1.99372	2.61170

利用本章介绍的几种插值方法对其进行插值，得到每隔0.05的结果。

2. 求函数 $$y=e^x-x^5$$， 初始点为 x = 8的解，并绘制图形。

3. 求下列函数的极值。
   （1） $$z=x^2-(y-1{)}^2$$
   （2） $$z=(x-y+1{)}^2$$

4. 计算下列积分。

(1) $${\int }_{-1}^{1}x+x^3+x^{5}dx$$

(2) $${\int }_1^{10}{\int }_1^{10}sin(y)\ast (x+y)/(x^2+4)dxdy$$