不同类型特征变量之间相关性分析
站在2022的第一天想说点啥总结却迟迟不知道该如何下笔,年前的立的各种风控技能Flag还没一一勾除又有新的Flag要立,风控人不容易…不管怎样,学习总是必要的,今天带来番茄风控2022年第一篇实操干货。
在数据分析过程中,对特征变量的相关性分析是一项重要工作,尤其是在数据建模场景,特征的相关性分析是变量筛选的一种典型方法。但是,在日常数据分析实践中,由于数据源的特征分布情况,特征相关性分析往往是针对连续变量与连续变量,如pearson相关系数等,而对分类变量的相关性较少关注。本文基于SAS实操,介绍下不同类型特征之间的相关性分析,分为三个部分:连续变量与连续变量、连续变量与分类变量、分类变量与分类变量。
现有一份excel测试数据,样本量2000,特征数13个,其结构如下图所示:

【图1:样本数据(前10条)】
通过以下代码进行excel数据导入,生成SAS数据集,并对数据的特征类型分布通过报表展示:

生成特征类型报表如图2所示,包括变量名称、类型、长度、标签等信息:
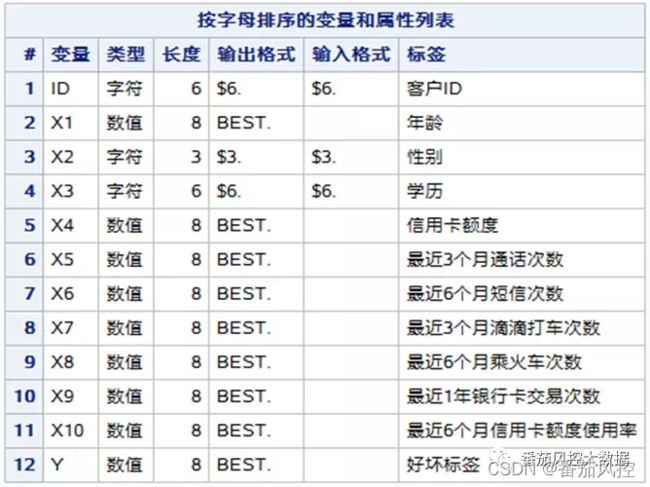 【图2:特征类型】
【图2:特征类型】
1、连续变量与连续变量
衡量连续变量与连续变量的相关性程度有多个参数,包括pearson、spearman、 kendall、hoeffding系数等,其中pearson是参数度量方法,spearman、kendall、hoeffding是非参数度量方法。在实际数据分析工作中,我们经常使用的是person系数或spearman系数。
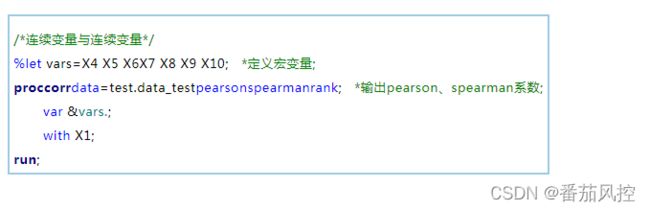
从图2信息可知,变量X1、X4X10均为连续型变量,我们通过SAS中的corr过程步分析变量X4X10与X1之间的线性相关程度。
代码运行后生成报表如图3~4所示,包括变量基本信息、统计信息(最大值、最小值、平均值、中位数、标准差等)、pearson系数、spearman系数。
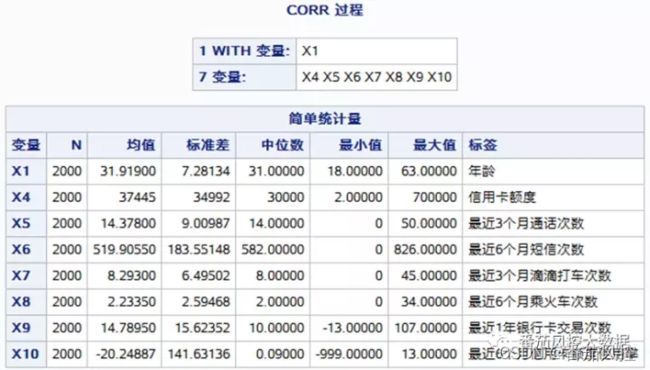

【图3: 统计信息】

【图4 :相关系数】
从上表可知,变量X4~X10与变量X1的相关性依次减弱,pearson系数与pearson系数均呈现同样规律。变量X1(年龄)与X4(信用卡额度)的相关性相对较强,从pearson系数0.12149与spearson系数0.23105均得以体现,同时p值(<0.0001)检验均远小于0.1。X1与X6、X7、X10的相关性均较弱,相关系数低于0.04,p值检验均大于0.1。
为了更有效评估连续变量之间的相关性,综合对比pearson系数与pearson系数更为合理些。例如,某两个变量之间的pearson系数较大,而pearson系数较小,则不能单从某一个系数大小评估其相关性程度。
2、连续变量与分类变量
连续变量与分类变量相关性程度的评估方法,有T检验、方差分析等。在SAS语言的统计分析中,主要取决于分类变量的类别数。若对比分类变量两个类别的差异,可以使用SAS中的ttest(T检验)过程;若比较分类变量多个类别的差异,可以使用anova(方差分析)过程。
T检验是通过T分布理论与假设检验原理进行样本均值与总体均值的比较,以及进行两样本均值的比较;方差分析是用于检验两组或两组以上样本的均值是否具有显著性差异性的一种数理统计方法。
2.1 二分类变量与连续变量
从图2的特征类型信息可知,变量Y(好坏标签)是二分类变量,X5(最近3个月通话次数)是连续型变量,我们通过SAS中的ttest过程步分析变量X2与X5之间的相关性程度。
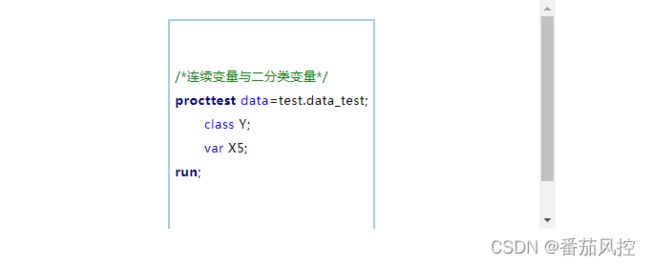
代码运行后生成报表如图5~ 6所示,包括变量统计信息(最大值、最小值、平均值、标准差、标准误差等)、置信区间、T检验、方差等价性检验。

图5: 统计信息与置信区间
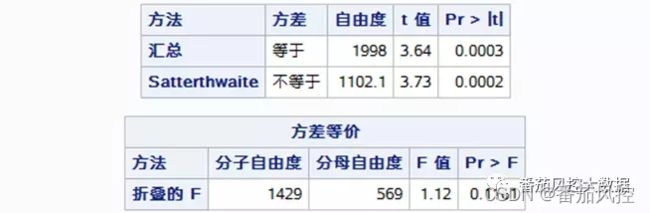
【图6 :T检验与方差等价检验】
根据生成的报表信息,我们来对结果指标进行解读。首先,看图6的“方差等价检验”结果,p值为0.1161,在0.1置信水平下,接受原假设,认为方差相等。然后,看图6 的“T检验”结果,在“方差”为“等于”的一行,对应p值为0.0003,在0.1置信水平下,拒绝原假设,认为变量Y的“0”和“1”两个群体间的“X5(最近3个月通话次数)”信息有显著性差异。最后,综上说明变量X5(最近3个月通话次数)可以作为区分Y变量(0或1)的一个有效特征,即两个变量之间有较好的相关性。
2.2 多分类变量与连续变量
以上是采用T检验,举例(Y与X5)对二分类变量与连续变量进行相关性分析。现选取多分类变量X3(学历)与连续变量X9(最近1年银行卡交易次数),通过SAS中的anova过程(方差分析)说明多分类变量与连续变量的相关性程度。

代码运行后生成报表如图7~9所示,包括方差分析、盒型图、方差齐性检验。根据图7方差分析结果可知,p值为0.9106,接受原假设,认为变量X3(学历)在7种不同水平下的X9(最近1年银行卡交易次数)信息没有显著性差异。从图9方差齐性检验结果可知,p值为0.9379,满足方差齐性检验,认为变量X3(学历)在7种不同水平下的X9(最近1年银行卡交易次数)信息没有较强的关联关系。图8变量盒型图则展示变量X3(学历)不同类别在X9(最近1年银行卡交易次数)的分布情况。
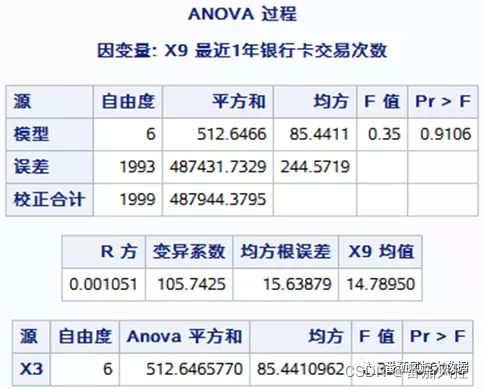
【图7:方差分析】

【图8:变量盒型图】
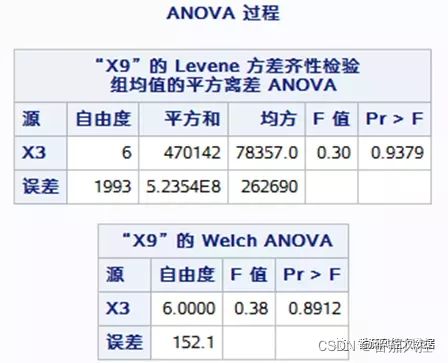
【图9:方差齐性检验】
3、分类变量与分类变量
分类变量之间的相关性检验,其理论基础为卡方检验分析,在SAS中以freq过程步(频数统计)实现分类变量相关性的分析过程。现选取分类变量X2(性别)与分类变量Y(好坏标签),对分类变量之间的相关性程度分析进行说明。

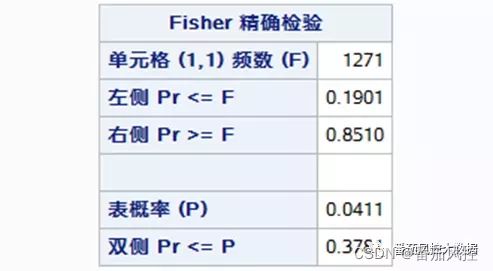
代码运行后生成如图10~13所示,包括变量交叉频数表、卡方检验、Fisher检验、优比信息,其中Fisher检验结果仅对于两个二分类变量输出,本例选取的两个分类变量均为二分类变量,即变量X2(性别)取值“男”与“女”,变量Y(好坏标签)取值“0”和“1”。
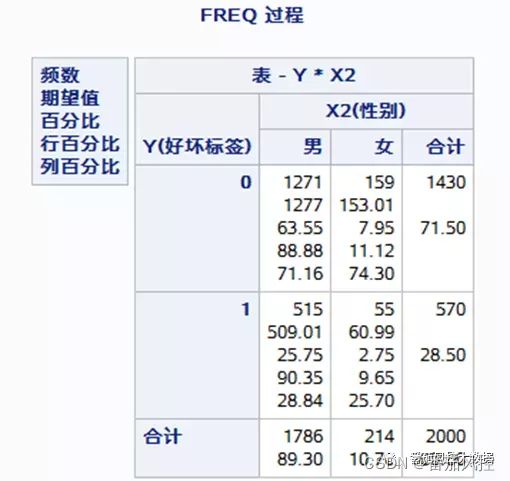
【图10:变量交叉频数 】
由图11卡方检验结果可知,p值为0.3371,在0.1置信水平下,接受原假设,认为分类变量X2(性别)与Y(好坏标签)无关联关系。由图12的Fisher检验可知,p值为0.3781,在0.1的置信水平下,接受原假设,认为X2(性别)与Y(好坏标签)无关联关系。由图13优化比信息可知,变量优比值为0.8537,而95%的置信区间为[0.6179, 1.1795],区间范围包含1,说明优比与1无显著性差异,即认为X2与Y无关联关系。综合以上三项指标,均说明X2(性别)与Y(好坏标签)无较强关联关系。
本文进一步的实操内容,更有相关的数据集提供给大家练习,详细的数据可以到星球进行下载学习:
另外关于本文中所提到的SAS相关的内容,更全面的系统知识可关注:
第一期的《SAS数据分析训练营》。
最后,感谢所有童鞋过去一年对番茄风控的关注~
祝大家元旦节快乐!