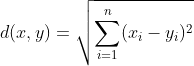【机器学习】1.逻辑回归模型(1)
目录
一、广义线性模型（Generalized Linear Model）
1、一个引例
2、定义
二、逻辑回归
1、对数几率模型（logit model）
2、逻辑回归与Sigmoid函数
三、逻辑回归模型的输出结果
四、逻辑回归的多分类拓展
1、OvO
2、OvR
3、MvM
一、广义线性模型（Generalized Linear Model）
1、一个引例
为现有函数关系，以线性方程进行预测
#构建数据集特征
np.random.seed(24)
x=np.linspace(0,5,25).reshape(-1,1)
x=np.concatenate((x,np.ones_like(x)),axis=1)
print(x)
#构建数据集标签
y=np.exp(x[:,0]+1).reshape(-1,1)
print(y)
#最小二乘法求解线性回归模型
w_b=np.linalg.lstsq(x,y,rcond=-1)[0]
print(w_b[0],w_b[1])
#输出预测值
y_hat=x[:,0]*w_b[0]+w_b[1]
print(y_hat)
#绘图展示
plt.plot(x[:,0],y,'o')
plt.plot(x[:,0],y_hat,'r-')
plt.show()
预测结果偏差较大，尝试线性方程的输出结果进行指数运算后对y进行预测（即用线性回归模型预测lny）
w_b2=np.linalg.lstsq(x,np.log(y),rcond=-1)[0]
print(w_b2[0],w_b2[1])
即 
以上实验所用的lny即为一个联系函数，以上模型也可以称为对数线性模型。
2、定义
一句话定义 广义线性模型 即：
In statistics, the generalized linear model (GLM) is a flexible generalization of ordinary linear regression that allows for response variables that have error distribution models other than a normal distribution.
详细来说，我们可以把 广义线性模型 分解为 Random Component、System Component 和 Link Function 三个部分。
通俗理解就是用函数连接线性方程的左右两端，使得原来线性模型的性能有所扩展
- 广义线性模型通常要求联系函数g(y)为单调可微函数，观测数据基本符合一些特定的数理统计分布（指数族分布）。 线性回归服从 Gaussian 高斯分布，逻辑回归服从 Bernoulli 伯努利分布。指数族还有很多分布如 多项分布、拉普拉斯分布、泊松分布等等。
- 广义线性模型 本质上还是线性模型。
- 通过 联系函数【g（y）】 建立 y和
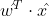俩者联系，联系函数（link function ）的反函数 g−1 称为 响应函数 response function。响应函数 把 linear predictor 直接映射到了预测目标 y，较常用的响应函数例如 logistic/sigmoid、softmax（都是 logit 的反函数）。
二、逻辑回归
1、对数几率模型（logit model）
几率：一个事件发生与不发生概率的比值。 
对数几率：几率取自然对数。 
逻辑回归模型（对数几率模型）：用对数几率作为联系函数的广义线性模型。
在数理统计中要求y服从伯努利分布。
2、逻辑回归与Sigmoid函数
将以上模型改写为y=f(x)的形式，以下为数学推导过程。
在此基础上可知，对数几率函数的反函数为
其函数图像如下
Sigmoid函数：如上述图像一样形如S的函数，Sigmoid函数是一个在生物学中常见的S型函数，也称为S型生长曲线。 在信息科学中，由于其单增以及反函数单增等性质，Sigmoid函数常被用作神经网络的激活函数，将变量映射到0,1之间，其中最为典型的是
3、Sigmoid函数的性质
是连续可导函数。来来来，高数它又来了，求导算性质
,Sigmoid函数的导函数可以用自身表示。
f'(x)的函数图像如下：
sigmoid函数导函数始终大于0，故sigmoid函数为单调递增函数。sigmoid函数取值为（0，1）。
导函数在0点取最大值，sigmoid函数在0点变化率最大。0点也是sigmoid函数的拐点。sigmoid函数当x趋近负无穷时，y趋近于0；趋近于正无穷时，y趋近于1；x=0时，y=0.5。当然，在x超出[-6,6]的范围后，函数值基本上没有变化，值非常接近，在应用中我们一般不考虑。
三、逻辑回归模型的输出结果
逻辑回归模型主要应用于二分类模型的预测。
二分类的判别通常取0.5为阈值
其中
为判别结果，y为逻辑回归方程的输出
| x | y | ycla |
| 3 | 0.12 | 0 |
| 0.3 | 0.67 | 1 |
逻辑回归模型有较好的可解释性，其中y的值可以被看做是一种概率。
其次逻辑回归方程变形一下：
左边的形式是不是在哪里见过？就是y的对数几率呀！x每增加1，y的对数几率就减少1
四、逻辑回归的多分类拓展
将上面的二分类模型改造一下
采用先拆分，后集成的策略：One vs Ons(OvO),One vs Rest(OvR),Many vs Many(MvM)
1、OvO
先依据标签不同拆分为四个小的数据集，再两两进行组合
共可能有六种情况。
将此四分类问题变成了6个二分类问题。
若数据集有N个类别，则拆分为
个数据集。
当6个二分类模型训练完成后，我们从6次训练结果中，选择0-3四个lable中频率最高的那一个。（投票法：每一次训练结果相当于投票给1个lable，最后得票最高的lables为最终判定的所属类别。）
如图所示，选定判定结果为2的概率最高（得票数最高），故判定新进入数据的labels为2。
2、OvR
拆分时选择特定一类作为类别1，其余所有类别作为类别2。可以拆分为4个二分类的分类器。
若数据集有N个类别，则拆分为N个数据集。
四类分类器的结果如何集成起来进行判定呢？
如图：选择判定结果为1的那个分类器对应的判定结果。R2分类器对应的判定lables为1，则新进入的数据判定结果标签为1。（如果有多个判定结果为1的分类器，则选择在训练集上准确率最高的那个分类器）
3、MvM
每次将若干类划为正类，若干类划为负类，多次划分，反复集成。
如下图：考虑将一个划为正，三个划为负的模型结果和三个划为正，一个划为负的模型结果相同。
本例中所有可能的划分结果为：
我们可以划分出10个数据集来构建10个分类器，在实际应用中我们采用ECOC（纠错输出编码），仅在所有划分结果中选部分来进行建模。本例我们选取4个进行建模。
例如k=10不大的时候可以使用穷举编码，在k大的时候可以使用随机编码等；并且分类器个数L = 矩阵长度d 满足
将正负例的标签组成的数组视为编码。（哈哈，发现了吗？labels相同的数据对应的编码是一样的）
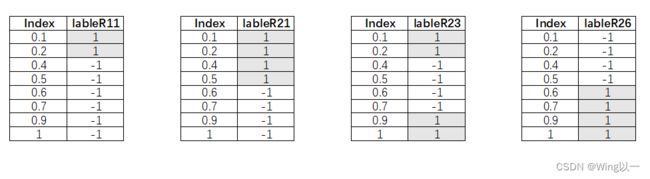
如何集成判定呢？如果新进入一个数据0.3，各分类器判定结果如下图，编码[1,1,1,-1]对应的labels为0。
ECOC框架中的编码矩阵，二元码用{-1，1}表示，三元码用{-1，0，1}表示。-1表示一类，1表示另一类。0表示该码字位对应的类在其列所形成的二分类划分中被忽略（即不参与这个分类器的训练）。
如果有一个编码并不能完全一一对应呢？(假如某个分类预测的部分预测不准确）
我们需要计算这个新编码与已知分类器对应编码的差距，找最相似的那一个。
距离计算公式参考如下：
![d(x,y)=\sqrt[n]{\sum_{i=1}^{n}(|x_{i}-y_{i}|)^{n}}](http://img.e-com-net.com/image/info8/72ec0cd769094e4eb36ac1d75177ccbf.gif)
最通用的情况下n=2
用numpy的相关方法实现距离计算
def dist(x,y,cat=2):
'''
计算两数组之间的距离minkowski distance
:param x: 数组x
:param y: 数组y
:param cat: minkowski distance中n
:return:距离
'''
d1=np.abs(x-y)
if x.ndim>1 or y.ndim>1: #维度判别
res1=np.power(d1,cat).sum(1) #对每一行进行求和
else:
res1=np.power(d1,cat).sum()
res= np.power(res1,1/cat)
return res#四个分类器对应的编码矩阵
code_classifier = np.array([[1,1,1,-1],[-1,1,-1,-1],[-1,-1,-1,1],[-1,-1,1,1]])
#新数据的预测编码
newdata_code = np.array([1,-1,1,1])
print(dist(code_classifier,newdata_code))
可见与lables=3对应的编码最相近。