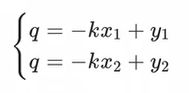python+OpenCV笔记（十八）：霍夫变换——霍夫线检测

目录

一、原理

直角坐标系

极坐标系

实现流程

二、霍夫线检测

代码编写

三、拓展

---

霍夫变换常用来提取图像中的直线和圆等几何形状，如下图所示：

一、原理

直角坐标系

   1.   

        在笛卡尔坐标系中，一条直线由两个点  和  确定。如下图所示：

         将直线  y = kx + q  可写成关于（k，q）的函数表达式：

        对应的变换通过图形直观的表示如下：

         变换后的空间我们叫做霍夫空间。即：笛卡尔坐标系中的一条直线，对应于霍夫空间中的一个点。

        反过来，同样成立，霍夫空间中的一条线，对应于笛卡尔坐标系中一个点，如下所示：

    2.   

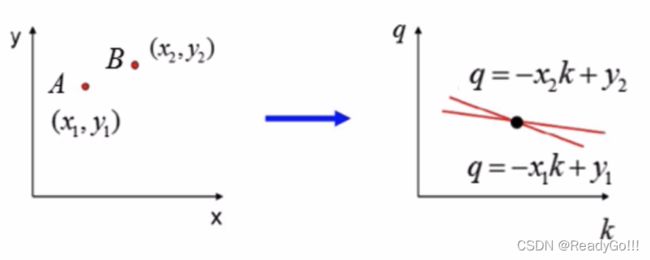
        我们再来看下A、B两个点，对应于霍夫空间的情形：

         再看下三点共线的情况：

         可以看出如果在笛卡尔坐标系的点共线，那么这些点在霍夫空间中对应的直线交于一点。

    3.   

        如果存在不止一条直线时，如下图所示：

         我们选择尽可能多的直线汇成的点，上图中三条直线汇成的A、B两点，将其对应回笛卡尔坐标系中的直线：

极坐标系

    1.   

        到这里我们似乎已经完成了霍夫变换的求解。但如果像下图这种情况时:

        上图中的直线为 x=2，那（k，q）怎么确定呢？

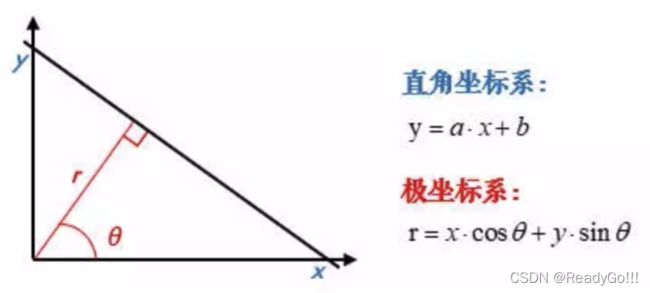
        为了解决这个问题，我们考虑将笛卡尔坐标系转换为极坐标。

     2.   

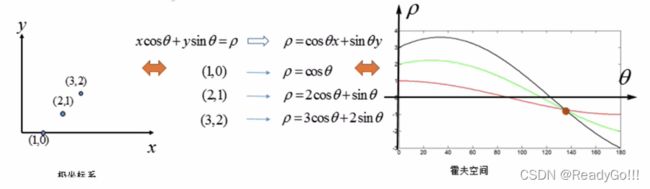
        在极坐标下是一样的，极坐标中的点对应于霍夫空间的线，这时的霍夫空间不是参数(k,q)的空间，而是(p,θ)的空间，p是原点到直线的垂直距离，θ表示直线的垂线与横轴顺时针方向的夹角，垂直线的角度为0度，水平线的角度是180度。

         我们只要求得霍夫空间中的交点的位置，即可得到原坐标系下的直线。

实现流程

        假设有一个大小为100*100的图片，使用霍夫变换检测图片中的直线，则步骤如下所示:

1. 直线都可以使用(p,θ)表示，首先创建一个2D数组，我们叫做累加器，初始化所有值为0，行表示p ，列表示θ。

   

   该数组的大小决定了结果的准确性，若希望角度的精度为1度，那就需要180列。对于p，最大值为图片对角线的距离，如果希望精度达到像素级别，行数应该与图像的对角线的距离相等。
2. 取直线上的第一个点(x，y)，将其带入直线在极坐标中的公式中，然后遍历θ的取值:0，1，2，..180，分别求出对应的p值，如果这个数值在上述累加器中存在相应的位置，则在该位置上加1。
3. 取直线上的第二个点，重复上述步骤，更新累加器中的值。对图像中的直线上的每个点都执行以上步骤，每次更新累加器中的值。
4. 搜索累加器中的最大值，并找到其对应的(p,θ)，就可将图像中的直线表示出来。

 例如：

        假定一个8*8的平面像素中有一条直线，如图：

         从左上角像素点（1,8）开始分别计算θ为0°，1°，2°......180°的ρ，从下图中可以看出ρ分别为1、...、(9√2)/2、...、8、...、(7√2)/2、...、-1，并给这181个值分别记一次，同理计算像素点(3,6)点的ρ，再给计算出来的181个ρ值分别记一票，此时就会发现ρ = (9√2)/2的这个值已经记了两次了，以此类推，遍历完整个8*8的像素空间的时候ρ = (9√2)/2就记了5次，别的ρ值的票数均小于5次，所以得到该直线在这个8*8的像素坐标中的极坐标方程为 (9√2)/2=x*cos45°+y*sin45°，到此该直线方程就求出来了。

二、霍夫线检测

OpenCV API:

cv2.HoughLines(image, rho, theta, threshold)

参数：

1. image：检测的图像，要求是二值化的图像。
                所以在调用霍夫变换前首先要进行二值化，或者进行Canny边缘检测。
2. rho，theta：ρ 和 θ 的精确度。
3. threshold：阈值，只有累加器中的值高于该值时才被认为是直线。

代码编写

import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np

src = cv.imread("E:\\Hough.png")
img = src.copy()

# 二值化图像（Canny边缘检测）
gray_img = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
dst_img = cv.Canny(gray_img, 50, 150)

# 霍夫线变换
lines = cv.HoughLines(dst_img, 0.5, np.pi / 180, 300)

# 将检测的线绘制在原图上（注意是极坐标）
for line in lines:
    rho, theta = line[0]
    a = np.cos(theta)
    b = np.sin(theta)
    # 找两个点
    x0 = rho * a
    y0 = rho * b
    x1 = int(x0 + 1000 * (-b))
    y1 = int(y0 + 1000 * a)
    x2 = int(x0 - 1000 * (-b))
    y2 = int(y0 - 1000 * a)
    cv.line(img, (x1, y1), (x2, y2), (0, 0, 255), 3)

# 显示图像
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(10, 8), dpi=100)
axes[0][0].imshow(src[:, :, ::-1])
axes[0][0].set_title("原图")
axes[0][1].imshow(dst_img, cmap=plt.cm.gray)
axes[0][1].set_title("Canny边缘检测结果")
# axes[1][0].imshow(img2[:, :, ::-1])
# axes[1][0].set_title("最终结果图（阈值150）")
axes[1][1].imshow(img[:, :, ::-1])
axes[1][1].set_title("最终结果图（阈值300）")
plt.show()

三、拓展

        OpenCV中还有一个检测线函数HoughLinesP，使用概率霍夫变换，它只分析图像点的子集，并估计这些点属于同一条线的概率，它是标准霍夫变换的优化版本，计算强度更小，执行速度更快。

        HoughLinesP的实现返回每个检测线段的两个端点（而HoughLines的实现返回每条线，表示形式为一个单点和一个角度，不包含端点的信息）。

代码示例： 

import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np

# 概率霍夫变换
src = cv.imread("E:\\Hough.png")
img = src.copy()
gray_img = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
dst_img = cv.Canny(gray_img, 20, 50)

lines = cv.HoughLinesP(dst_img, 1, np.pi / 180, 20)

for x1, y1, x2, y2 in lines[0]:
    cv.line(img, (x1, y1), (x2, y2), (0, 255, 0), 3)

cv.imshow("HoughLinesP", img)
cv.waitKey(0)