tensorflow学习
Tensorflow API
关于Weight decay 的作用
关于softmax()的函数
softmax模型可以用来给不同的对象分配概率。即使在之后,我们训练更加精细的模型时,最后一步也需要用softmax来分配概率。
为了得到一张给定图片属于某个特定数字类的证据(evidence),我们对图片像素值进行加权求和。如果这个像素具有很强的证据说明这张图片不属于该类,那么相应的权值为负数,相反如果这个像素拥有有利的证据支持这张图片属于这个类,那么权值是正数。
我们也需要加入一个额外的偏置量(bias),因为输入往往会带有一些无关的干扰量。因此对于给定的输入图片 x 它代表的是数字 i 的证据可以表示为
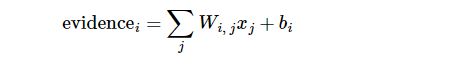
其中 代表权重, 代表数字 i 类的偏置量,j 代表给定图片 x 的像素索引用于像素求和。然后用softmax函数可以把这些证据转换成概率 y:
对于每个evidence 是需要对所有像素点进行加权的,而不是单独一个。
例如y1,y2,y3 加入有3个输出值,那么有一组权值
w11 ,w12,w13 与y1对应
w21, w22 ,w23 与y2对应
w31, w32 ,w33 与y3对应
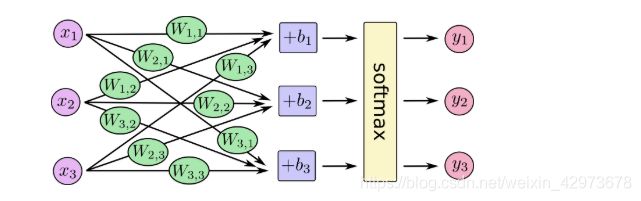
图1
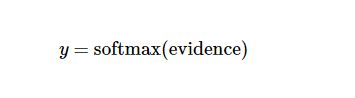
这里的softmax可以看成是一个激励(activation)函数或者链接(link)函数,把我们定义的线性函数的输出转换成我们想要的格式,也就是关于10个数字类的概率分布。因此,给定一张图片,它对于每一个数字的吻合度可以被softmax函数转换成为一个概率值。softmax函数可以定义为:

所以上图可以转化为如下:


在真实的实验里,我们的输入x = [x1, x2, x3] b=[b1,b2,b3]
我们希望输出的结果为[y1,y2,y3]
所以实际计算是
y = softmax(xW + b)
其中W =
[
[w11,w12,w13],
[w21,w22,w23],
[w31,w32,w33]
]
如果是这样写的话,那么上面的对应关系要变为:
w11 ,w21,w31 与y1对应
w12, w22 ,w32 与y2对应
w13, w23 ,w33 与y3对应
即w_,j 列的权值对应yj 的值
这样图1要改了,但是我懒得画了
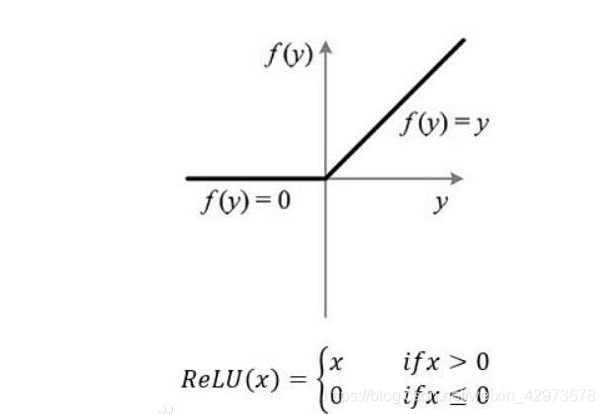
tf.nn.relu()函数是将大于0的数保持不变,小于0的数置为0
tf.truncated_normal与tf.random_normal
1、tf.truncated_normal(shape, mean=0.0, stddev=1.0, dtype=tf.float32, seed=None, name=None)
从截断的正态分布中输出随机值。
生成的值服从具有指定平均值和标准偏差的正态分布,如果生成的值大于平均值2个标准偏差的值则丢弃重新选择
在正态分布的曲线中,横轴区间(μ-σ,μ+σ)内的面积为68.268949%。
横轴区间(μ-2σ,μ+2σ)内的面积为95.449974%。
横轴区间(μ-3σ,μ+3σ)内的面积为99.730020%。
X落在(μ-3σ,μ+3σ)以外的概率小于千分之三,在实际问题中常认为相应的事件是不会发生的,基本上可以把区间(μ-3σ,μ+3σ)看作是随机变量X实际可能的取值区间,这称之为正态分布的“3σ”原则。
在tf.truncated_normal中如果x的取值在区间(μ-2σ,μ+2σ)之外则重新进行选择。这样保证了生成的值都在均值附近。
- shape:张量的形状。
- mean: 正态分布的均值。
- stddev: 正态分布的标准差。
- dtype: 输出的类型。
- seed: 一个整数,当设置之后,每次生成的随机数都一样。
- name: 操作的名字。
2、tf.random_normal(shape, mean=0.0, stddev=1.0, dtype=tf.float32, seed=None, name=None)
从正态分布中输出随机值。
参数:
- shape: 输出的张量。
- mean: 正态分布的均值。
- stddev: 正态分布的标准差。
- dtype: 输出的类型。
- seed: 一个整数,当设置之后,每次生成的随机数都一样。
- name: 操作的名字。
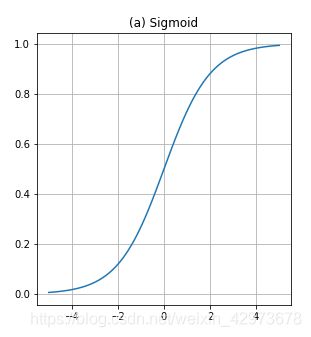
tf.nn.sigmoid()
input_data = tf.Variable( [[0, 10, -10],[1,2,3]] , dtype = tf.float32 )
output = tf.nn.sigmoid(input_data)
with tf.Session() as sess:
init = tf.initialize_all_variables()
sess.run(init)
print(sess.run(output))
[[5.0000000e-01 9.9995458e-01 4.5397868e-05]
[7.3105860e-01 8.8079703e-01 9.5257413e-01]]
函数:tf.slice(inputs, begin, size, name)
作用:从列表、数组、张量等对象中抽取一部分数据
begin和size是两个多维列表,他们共同决定了要抽取的数据的开始和结束位置
begin表示从inputs的哪几个维度上的哪个元素开始抽取
size表示在inputs的各个维度上抽取的元素个数
x=[[1,2,3],[4,5,6],[7,8,9]]
'''
1 2 3
4 5 6
7 8 9
'''
with tf.Session() as sess:
begin = [1,1] # 从x[1,1],指定从1行1列之后截取
size = [2,2] # 从x[1,1]开始,对x的第一个维度(行)抽取2个元素(即2行),在对x的第二个维度(列)抽取1个元素(即每行,从指定的列之后取)
print(sess.run(tf.slice(x,begin,size))) # 输出[[2 5]]
[[5 6]
[8 9]]
总结一下:假定我们是2维的,多维同理,扩展begin 和size就好
x=[w,h]
begin = [row,col] // 表示从第row 行,col列之后获取数据
size = [nrow,ncol] // 这里其实对nrow 和ncol 有限制
即nrow< = h - row ncol<=w-col
reduce_prod(input_tensor,axis=None,keep_dims=False,name=None,reduction_indices=None
此函数计算一个张量的各个维度上元素的乘积。
函数中的input_tensor是按照axis中已经给定的维度来减少的;除非 keep_dims 是true,否则张量的秩将在axis的每个条目中减少1;如果keep_dims为true,则减小的维度将保留为长度1。
如果axis没有条目,则缩小所有维度,并返回具有单个元素的张量。
此函数计算一个张量的各个维度上元素的乘积。
x1 =[[1,2,3],[4,5,6]]
#这里的举例是二维矩阵
with tf.Session() as sess:
print(sess.run(tf.reduce_prod(x1))) # 全部元素相乘
print(sess.run(tf.reduce_prod(x1,axis=0))) # 合并行,按行相乘
print(sess.run(tf.reduce_prod(x1,axis=1))) # 合并列,按列相乘
结果:
720
[ 4 10 18]
[ 6 120]
x1 =[[[1,2,3,4],
[1,2,3,4]], # 一个平面
[[0,0,0,0],
[1,1,1,1]]] # 第二个平面
print(sess.run(tf.reduce_prod(x1))) # 全部元素相乘
print(sess.run(tf.reduce_prod(x1,axis=0))) #合并平面,按平面相乘
print(sess.run(tf.reduce_prod(x1,axis=1))) #合并行,按行相乘
结果:
0
[[0 0 0 0]
[1 2 3 4]]
[[ 1 4 9 16]
[ 0 0 0 0]]
总结一下,如果不加axis就全部相乘,否则,指定一个维度,就会消去那个维度,实现降维
max的结果
print(sess.run(tf.reduce_max(x1))) # 全部元素相乘
print(sess.run(tf.reduce_max(x1,axis=0)))
print(sess.run(tf.reduce_max(x1,axis=1)))
4
[[1 2 3 4]
[1 2 3 4]]
[[1 2 3 4]
[1 1 1 1]]
tf.reduce_sum() 求和,道理同上
tf.reduce_mean () 求平均值,道理同上
tf.reduce_max()求最大值,道理同上
tf.reduce_min()求最小值,道理同上
tf.concat([tensor1, tensor2, tensor3,…], axis)
t1 = [[1, 2, 3], [4, 5, 6]]
t2 = [[7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 0) # [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 1) # [[1, 2, 3, 7, 8, 9], [4, 5, 6, 10, 11, 12]]
# tensor t1 with shape [2, 3]
# tensor t2 with shape [2, 3]
tf.shape(tf.concat([t1, t2], 0)) # [4, 3]
tf.shape(tf.concat([t1, t2], 1)) # [2, 6]
axis=0 代表在第0个维度拼接
axis=1 代表在第1个维度拼接
tf.concat()拼接的张量只会改变一个维度,其他维度是保存不变的。
显然,就是指定axis,那么就其他维度不变,把axis累加就行。
random.sample(list,num)
在指定范围内,随机选出num个元素返回
a = [11,22,33,43,53,63,73,83,93,103]
idx = random.sample(range(len(a)),3)
elem = random.sample(a,3) # 返回元素
print(idx) # 返回的是下标
print(elem)
[4, 6, 1] //返回索引
[83, 93, 33] //返回元素
d = np.array([[1,2,3],[4,5,6],[7,8,9]])
c = np.zeros((4,3))
a = np.zeros((5,1),np.float32)
idx = random.sample(range(len(d)),2)
c[:2,:] = d[idx,:]
//第一维表示从0-1 idx的长度要跟他一样,只要后面的元素和维度一样,就表明依次赋值
print(a)
print(c)
[[0.]
[0.]
[0.]
[0.]
[0.]]
[[1. 2. 3.]
[4. 5. 6.]
[0. 0. 0.]
[0. 0. 0.]]
np.vstack() 的理解
np.hstack():水平方向排列数组,行数不变,列数增加。一般用于三维以下的数组。
np.vstack():垂直方向排列数组,列数不变,行数增加。一般用于三维以下的数组。
a = [[0 1 2]
[3 4 5]]
b = [[0 1 2]
[3 4 5]]
c = np.hstack((a, b)) # c.shape=(2,6)
d = np.vstack((a, b)) # d.shape=(4,3)
c = [[0 1 2 0 1 2]
[3 4 5 3 4 5]]
d 列 = a 列 = b 列 d 行 = a 行 + b 行
d = [[0 1 2]
[3 4 5]
[0 1 2]
[3 4 5]]
numpy.where()
1. np.where(condition, x, y)
满足条件(condition),输出x,不满足输出y。 对数组进行转化
a = np.arange(10)
a1 = np.where(a>5,1,0)
print(a1)
[0 0 0 0 0 0 1 1 1 1]
2. np.where(condition)
返回满足条件的索引
a = np.arange(10)
idx = np.where(a>5) # 返回值是一个array(index,type)
print(idx[0])
print(a[a[np.where(a > 5)]]) # 与上面相同,打印对应的值
print(a[a>5])
三种输出都一样
[6 7 8 9]
------------------------------------
看一个复杂一点的
a = np.arange(8).reshape(2,2,2)
idx = np.where(a>3)
print(a[idx])
(array([1, 1, 1, 1], dtype=int64), //对应第一维
array([0, 0, 1, 1], dtype=int64), //对应第二维
array([0, 1, 0, 1], dtype=int64)) //对应第三维
[4 5 6 7]
np.maximum(num,list)
返回值是一个list
xx1 = np.maximum(1,[-1,1,2,3,-4])
[1 1 2 3 1]
numpy.delete(arr,obj,axis=None)
arr:输入数组
obj:切片,整数,表示哪个子数组要被移除
axis:删除子数组的轴
axis = 0:表示删除数组的行
axis = 1:表示删除数组的列
axis = None:表示把数组按一维数组平铺在进行索引删除
x = np.array(
[[1,2,3],
[4,5,6],
[7,8,9]])
# 删除第i 行
x1 = np.delete(x,2,axis=0)
print(x1)
[[1 2 3]
[4 5 6]]
# 删除多行
x2 = np.delete(x,[1,2],axis=0)
print(x2)
[[1 2 3]]
# 删除第j 列
c1 = np.delete(x,2,axis=1)
print(c1)
[[1 2]
[4 5]
[7 8]]
# 删除多列
c2 = np.delete(x,[1,2],axis=1)
print(c2)
[[1]
[4]
[7]]
# 展平按索引删除
x = np.delete(x,[1,2,3])
print(x)
[1 5 6 7 8 9]
tf.gfile.GFile(filename, mode)
获取文本操作句柄,类似于python提供的文本操作open()函数,filename是要打开的文件名,mode是以何种方式去读写,将会返回一个文本操作句柄。
with tf.gfile.GFile(image_path, 'rb') as f:
encoded_jpg = f.read()
tf.train.Example
主要用在将数据处理成二进制方面,一般是为了提升IO效率和方便管理数据。下面按调用顺序介绍使用tf.train.Example涉及的几个类。
tf.train.BytesList等
现在我们有一个data.txt文件,内容如下:
1
hello solicucu
hhh
文件中第一行是个整数,第二行和第三行都是字符串。
格式化原始数据可以使用tf.train.BytesList tf.train.Int64List tf.train.FloatList三个类。
这三个类都有实例属性value用于我们将值传进去,一般tf.train.Int64List tf.train.FloatList对应处理整数和浮点数,tf.train.BytesList用于处理其他类型的数据。
这里第一行数据我们可以用tf.train.Int64List处理,而第二、第三行数据我们使用tf.train.BytesList处理。
file = open("test.txt")
line = file.readlines().strip()
data_id = tf.train.Int64List(value=[int(line[0])])
data = tf.train.BytesList(value=[bytes(' '.join(line[1:]), encoding='utf-8')])
#注意到,tf.train.Int64List的value值需要是int数据的列表,而tf.train.BytesList的value值需要是bytes数据的列表。
tf.train.Features
事实上tf.train.Features有属性为feature,这个属性的一般设置方法是传入一个字典,字典的key是字符串(feature名),而值是tf.train.Feature对象。因此,我们可以这样得到tf.train.Features对象:
feature_dict = {
"data_id": tf.train.Feature(int64_list=data_id),
"data": tf.train.Feature(bytes_list=data)
}
features = tf.train.Features(feature=feature_dict)
tf.train.Example
tf.train.Example有一个属性为features,我们只需要将上一步得到的结果再次当做参数传进来即可。
另外,tf.train.Example还有一个方法SerializeToString()需要说一下,这个方法的作用是把tf.train.Example对象序列化为字符串,因为我们写入文件的时候不能直接处理对象,需要将其转化为字符串才能处理。
当然,既然有对象序列化为字符串的方法,那么肯定有从字符串反序列化到对象的方法,该方法是FromString(),需要传递一个tf.train.Example对象序列化后的字符串进去做为参数才能得到反序列化的对象。
在我们这里,只需要构建tf.train.Example对象并序列化就可以了,这一步的代码为:
example = tf.train.Example(features=features)
example_str = example.SerializeToString()
Tensorflow: 批标准化(Batch Normalization)
背景
批标准化(Batch Normalization )简称BN算法,是为了克服神经网络层数加深导致难以训练而诞生的一个算法。根据ICS理论,当训练集的样本数据和目标样本集分布不一致的时候,训练得到的模型无法很好的泛化。
而在神经网络中,每一层的输入在经过层内操作之后必然会导致与原来对应的输入信号分布不同,并且前层神经网络的增加会被后面的神经网络不对的累积放大。这个问题的一个解决思路就是根据训练样本与目标样本的比例对训练样本进行一个矫正,而BN算法(批标准化)则可以用来规范化某些层或者所有层的输入,从而固定每层输入信号的均值与方差。
import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
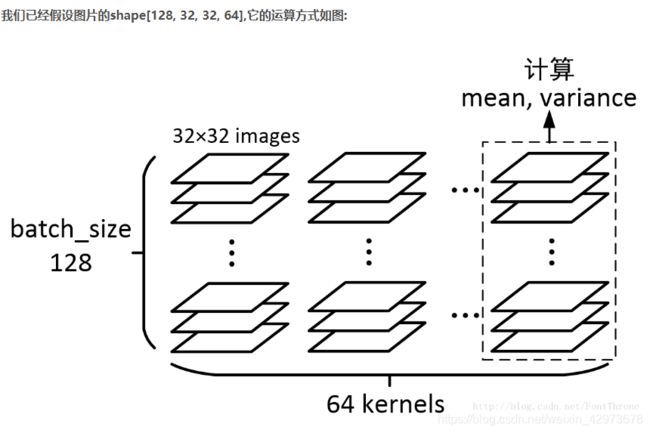
# 计算Wx_plus_b 的均值与方差,其中axis = [0] 表示想要标准化的维度
img_shape = [128, 32, 32, 64]
Wx_plus_b = tf.Variable(tf.random_normal(img_shape))
axis = list(range(len(img_shape) - 1))
wb_mean, wb_var = tf.nn.moments(Wx_plus_b, axis)
scale = tf.Variable(tf.ones([64]))
offset = tf.Variable(tf.zeros([64]))
variance_epsilon = 0.001
Wx_plus_b0 = tf.nn.batch_normalization(Wx_plus_b, wb_mean, wb_var, offset, scale, variance_epsilon)
# 根据公式我们也可以自己写一个
Wx_plus_b1 = (Wx_plus_b - wb_mean) / tf.sqrt(wb_var + variance_epsilon)
Wx_plus_b1 = Wx_plus_b1 * scale + offset
# 因为底层运算方式不同,实际上自己写的最后的结果与直接调用tf.nn.batch_normalization获取的结果并不一致
with tf.Session() as sess:
tf.global_variables_initializer().run()
print('*** wb_mean ***')
print(sess.run(wb_mean))
print('*** wb_var ***')
print(sess.run(wb_var))
print('*** Wx_plus_b ***')
print(sess.run(Wx_plus_b0))
print('**** Wx_plus_b1 ****')
print(sess.run(Wx_plus_b1))
---------------------
作者:Font Tian
来源:CSDN
原文:https://blog.csdn.net/FontThrone/article/details/76652772
版权声明:本文为博主原创文章,转载请附上博文链接!
slim.arg_scope()
函数的使用
slim是一种轻量级的tensorflow库,可以使模型的构建,训练,测试都变得更加简单。在slim库中对很多常用的函数进行了定义,slim.arg_scope()是slim库中经常用到的函数之一
def arg_scope(list_ops_or_scope, **kwargs):
"""Stores the default arguments for the given set of list_ops.
For usage, please see examples at top of the file.
Args:
list_ops_or_scope: List or tuple of operations to set argument scope for or
a dictionary containing the current scope. When list_ops_or_scope is a
dict, kwargs must be empty. When list_ops_or_scope is a list or tuple,
then every op in it need to be decorated with @add_arg_scope to work.
**kwargs: keyword=value that will define the defaults for each op in
list_ops. All the ops need to accept the given set of arguments.
Yields:
the current_scope, which is a dictionary of {op: {arg: value}}
Raises:
TypeError: if list_ops is not a list or a tuple.
ValueError: if any op in list_ops has not be decorated with @add_arg_scope.
"""
如注释中所说,这个函数的作用是给list_ops中的内容设置默认值。但是每个list_ops中的每个成员需要用@add_arg_scope修饰才行。所以使用slim.arg_scope()有两个步骤:
1 、使用@slim.add_arg_scope修饰目标函数
2 、用 slim.arg_scope()为目标函数设置默认参数.
例如如下代码;首先用@slim.add_arg_scope修饰目标函数fun1(),然后利用slim.arg_scope()为它设置默认参数。
import tensorflow as tf
slim =tf.contrib.slim
@slim.add_arg_scope
def fun1(a=0,b=0):
return (a+b)
with slim.arg_scope([fun1],a=10):
x=fun1(b=30)
print(x)
result = 40
平常所用到的slim.conv2d( ),slim.fully_connected( ),slim.max_pool2d( )等函数在他被定义的时候就已经添加了@add_arg_scope。
'''
在使用过程中可以直接slim.conv2d( )等函数设置默认参数。例如在下面的代码中,不做单独声明的情况下,
slim.conv2d, slim.max_pool2d, slim.avg_pool2d三个函数默认的步长都设为1,padding模式都是'VALID'的。
但是也可以在调用时进行单独声明。这种参数设置方式在构建网络模型时,尤其是较深的网络时,可以节省时间
'''
with slim.arg_scope(
[slim.conv2d, slim.max_pool2d, slim.avg_pool2d],stride = 1, padding = 'VALID'):
net = slim.conv2d(inputs, 32, [3, 3], stride = 2, scope = 'Conv2d_1a_3x3')
net = slim.conv2d(net, 32, [3, 3], scope = 'Conv2d_2a_3x3')
net = slim.conv2d(net, 64, [3, 3], padding = 'SAME', scope = 'Conv2d_2b_3x3')
@修饰符
其实这种用法是python中常用到的。在python中@修饰符放在函数定义的上方,它将被修饰的函数作为参数,
并返回修饰后的同名函数。形式如下;
@fun_a #等价于fun_a(fun_b)
def fun_b():
def funs(fun,factor=20):
x=fun()
print(factor*x)
@funs #等价funs(add(),fator=20)
def add(a=10,b=20):
return(a+b)
tf.gfile模块的主要角色是:
1.提供一个接近Python文件对象的API,以及
2.提供基于TensorFlow C ++ FileSystem API的实现。
C ++ FileSystem API支持多种文件系统实现,包括本地文件,谷歌云存储(以gs://开头)和HDFS(以hdfs:/开头)。 TensorFlow将它们导出为tf.gfile,以便我们可以使用这些实现来保存和加载检查点,编写TensorBoard log以及访问训练数据(以及其他用途)。但是,如果所有文件都是本地文件,则可以使用常规的Python文件API而不会造成任何问题
API 功能描述:
1、tf.gfile.Copy(oldpath, newpath, overwrite=False)
拷贝源文件并创建目标文件,无返回,其形参说明如下:
oldpath:带路径名字的拷贝源文件;
newpath:带路径名字的拷贝目标文件;
overwrite:目标文件已经存在时是否要覆盖,默认为false,如果目标文件已经存在则会报错
2、tf.gfile.MkDir(dirname)
创建一个目录,dirname为目录名字,无返回。
3、tf.gfile.Remove(filename)
删除文件,filename即文件名,无返回。
4、tf.gfile.DeleteRecursively(dirname)
递归删除所有目录及其文件,dirname即目录名,无返回。
5、tf.gfile.Exists(filename)
判断目录或文件是否存在,filename可为目录路径或带文件名的路径,有该目录则返回True,否则False。
6、tf.gfile.Glob(filename)
查找匹配pattern的文件并以列表的形式返回,filename可以是一个具体的文件名,也可以是包含通配符的正则表达式。
7、tf.gfile.IsDirectory(dirname)
判断所给目录是否存在,如果存在则返回True,否则返回False,dirname是目录名。
8、tf.gfile.ListDirectory(dirname)
罗列dirname目录下的所有文件并以列表形式返回,dirname必须是目录名。
9、tf.gfile.MakeDirs(dirname)
以递归方式建立父目录及其子目录,如果目录已存在且是可覆盖则会创建成功,否则报错,无返回。
10、tf.gfile.Rename(oldname, newname, overwrite=False)
重命名或移动一个文件或目录,无返回,其形参说明如下:
oldname:旧目录或旧文件;
newname:新目录或新文件;
overwrite:默认为false,如果新目录或新文件已经存在则会报错,否则重命名或移动成功。
11、tf.gfile.Stat(filename)
返回目录的统计数据,该函数会返回FileStatistics数据结构,以dir(tf.gfile.Stat(filename))获取返回数据的属性如下:
12、tf.gfile.Walk(top, in_order=True)
递归获取目录信息生成器,top是目录名,in_order默认为True指示顺序遍历目录,否则将无序遍历,每次生成返回如下格式信息(dirname, [subdirname, subdirname, …], [filename, filename, …])。
13、tf.gfile.GFile(filename, mode)
获取文本操作句柄,类似于python提供的文本操作open()函数,filename是要打开的文件名,mode是以何种方式去读写,将会返回一个文本操作句柄。
tf.gfile.Open()是该接口的同名,可任意使用其中一个!
14、tf.gfile.FastGFile(filename, mode)
该函数与tf.gfile.GFile的差别仅仅在于“无阻塞”,即该函数会无阻赛以较快的方式获取文本操作句柄。
np.squeeze 函数
从数组的形状中删除单维度条目,即把shape中为1的维度去掉
用法:numpy.squeeze(a,axis = None)
1)a表示输入的数组;
2)axis用于指定需要删除的维度,但是指定的维度必须为单维度,否则将会报错;
3)axis的取值可为None 或 int 或 tuple of ints, 可选。若axis为空,则删除所有单维度的条目;
4)返回值:数组
5) 不会修改原数组;
>>> a = e.reshape(1,1,10)
>>> a
array([[[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]])
>>> np.squeeze(a)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])