一文了解PnP算法，python opencv中的cv2.solvePnP()的使用，以及使用cv2.sovlePnP()方法标定相机和2D激光雷达

1 pnp算法概念和原理介绍

1.1 pnp算法的概念

下面几种说法都是对pnp算法要做的事情的描述，大家自己体会一下

1、PnP（Perspective-n-Point）是求解 3D 到 2D 点对运动的方法。它描述了当我们知道n 个 3D 空间点以及它们的投影位置时，如何估计相机所在的位姿。——《视觉SLAM十四讲》（参考）

2、通俗的讲，PnP问题就是在已知世界坐标系下N个空间点的真实坐标以及这些空间点在图像上的投影，如何计算相机所在的位姿。罗嗦一句：已知量是空间点的真实坐标和图像坐标，未知量（求解量）是相机的位姿。

3、PnP是用来求解3D-2D点对运动的方法（参考）

4、PnP问题就是指通过世界中的N个特征点与图像成像中的N个像点，计算出其投影关系，从而获得相机或物体位姿的问题（参考）

1.2 pnp算法的概念总结

下面我在来简单总结一下我个人的理解（参考）：

图片来源

使用Perspective-n-Point (PnP)算法需要知道的已知量和需要求解的未知量：

1.2.1 PnP需要知道的已知量

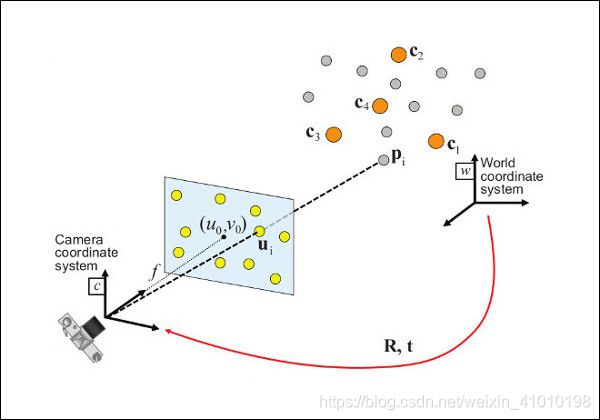
1、需要知道n个世界坐标系下参考点的3D坐标系：$\left\{c_1,c_2,c_3,...,c_n\right\}$

2、同时知道这个n个3D坐标对应相机图像坐标系上的2D投影点：$\left\{u_1,u_2,u_3,...,u_n\right\}$

注意：

• 世界坐标系下的3D点和相机坐标系下投影的2D点是一一对应的
• 相机图像坐标系，并不是相机坐标系或相机像素坐标系，注意区分

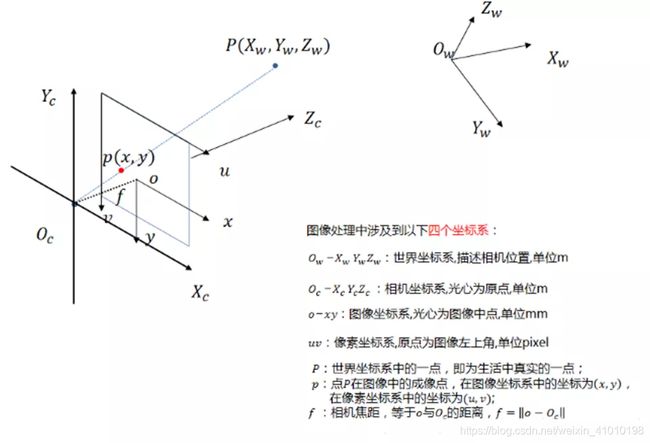
下图是四大坐标系：

3、已知相机摄像头的内参（需要自己提前标注好），相机的摄像头内参包括两部分;

• 相机的内参矩阵
• 相机畸变系数

内参矩阵：

$$\text{ camera matrix }=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$

焦距$（f_x,f_y）$和光学中心$（c_x,c_y）$

畸变系数：

• $k_1、k_2、k_3$：是径向畸变
• $p_1、p_2$：是切向畸变

1.2.2 PnP需要求的未知量

求世界坐标系与摄像机坐标系之间的位姿变换 ：$\left\{R|t\right\}$

• R：是旋转矩阵，可以理解为绕x、y、z三个坐标轴方向的旋转
• t：是平移，可以理解为沿x、y、z三个方向上的平移

所以从一个坐标系变换到另外一个坐标系的位姿变换的自由度就是6，三个方向上的旋转和三个方向上的平移。（参考）

1.3 PnP算法的用处

从上面可以知道PnP就是计算出两个坐标系之间的位姿变换的：$\left\{R|t\right\}$

因此PnP用途也很多：

• 相机位姿跟踪
• 物体位姿跟踪
• AR/VR、
• 机器人操作
• SLAM中位姿初值求解
• 相机标定，相机和激光雷达联合标定等

2 PnP的常见解法

PnP的常用解法也有很多：DLT，P3P，EPnP，UPnP

2.1 PnP解法之DLT

• 参考：https://zhuanlan.zhihu.com/p/58648937

2.2 PnP解法之P3P

• 参考：https://www.jianshu.com/p/b3e9fb2ad0dc

上面的文章中还介绍了很多其他的解法

2.3 PnP解法之EPnP

• 参考：https://blog.csdn.net/jessecw79/article/details/82945918

PnP问题是研究如何从3D-2D匹配对中求解摄像头位姿，EPnP算法是一种非迭代的PnP算法

3 opencv中solvePn()函数的介绍与使用

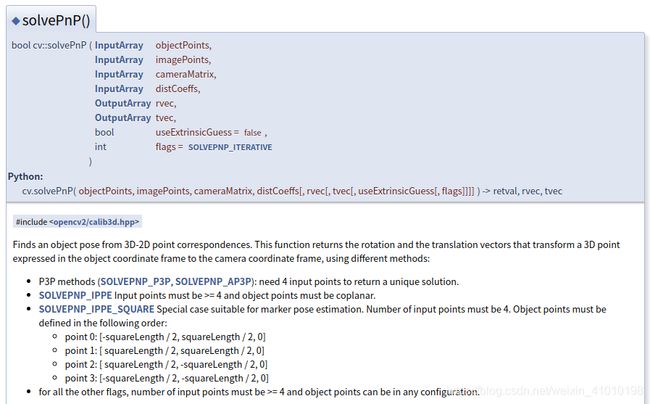
3.1 opencv中solvePnP函数的定义

1、在opencv中的slovePnP函数的定义：

3.2 solvePnP()中参数含义：

• 参考：https://blog.csdn.net/cocoaqin/article/details/77485436
• 参考：https://blog.csdn.net/u010554381/article/details/81983992
• 参考：https://blog.csdn.net/cocoaqin/article/details/77848588

3.2.1 solvePnP()中的参数

1、下面是solvePnP()函数参数含义解释（参考）：

• objectPoints：特征点的世界坐标，坐标值需为float型，不能为double型，可以为mat类型，也可以直接输入vector

• imagePoints：特征点在图像中的像素坐标，可以输入mat类型，也可以直接输入vector，注意输入点的顺序要与前面的特征点的世界坐标一一对应

• cameraMatrix：相机内参矩阵

• distCoeffs：相机的畸变参数【Mat_(5, 1)】

• rvec：输出的旋转向量：

• tvec：输出的平移向量

• useExtrinsicGuess： 用于SOLVEPNP迭代的参数。如果为true（1），函数使用提供的rvec和tvec值分别作为旋转和平移向量的初始近似，并进一步优化它们。默认值为False。

• flags：PnP的计算方法

3.2.2 sovlePnP()中flags参数对应的PnP计算方法

flags取值对应的是PnP的计算方法，flags的参数选择（参考）：

enum { SOLVEPNP_ITERATIVE = 0,
       SOLVEPNP_EPNP      = 1, //!< EPnP: Efficient Perspective-n-Point Camera Pose Estimation @cite lepetit2009epnp
       SOLVEPNP_P3P       = 2, //!< Complete Solution Classification for the Perspective-Three-Point Problem 
       SOLVEPNP_DLS       = 3, //!< A Direct Least-Squares (DLS) Method for PnP  @cite hesch2011direct
       SOLVEPNP_UPNP      = 4, //!< Exhaustive Linearization for Robust Camera Pose and Focal Length Estimation 
       SOLVEPNP_AP3P      = 5, //!< An Efficient Algebraic Solution to the Perspective-Three-Point Problem 
       SOLVEPNP_MAX_COUNT      //!< Used for count
};

1、cv2.SOLVEPNP_ITERATIVE=0

SOLVEPNP_ITERATIVE的迭代方法是基于Levenberg-Marquardt优化。 在这种情况下，函数会找到一个使重新投影误差最小的位姿（pose），该位姿是观察到的投影imagePoints与使用projectPoints将objectPoints投影的点之间的平方距离的总和（参考）。

Levenberg-Marquardt法（LM法）是一种非线性优化方法。LM算法用于解决非线性最小二乘问题，多用于曲线拟合等场合

2、cv2.SOLVEPNP_EPNP=1

3、cv2.SOLVEPNP_P3P=2

4、cv2.SOLVEPNP_DLS=3

5、cv2.SOLVEPNP_UPNP=4

6、cv2.SOLVEPNP_AP3P=5

3.3 如何获取世界坐标和图像坐标

• 参考：https://blog.csdn.net/cocoaqin/article/details/77848588

3.4 如何标定相机的内参（内参矩阵和畸变系数）

3.5 solvePnP()的实际使用实例

参考：https://blog.csdn.net/lyhbkz/article/details/90246356
参考：https://blog.csdn.net/shenxiaolu1984/article/details/50165635

3.5.1 使用solvePnP()标定相机和2D lidar激光雷达

camera_2d_lidar_calibration

cv2.solvePnP(objp, imgp, K, D, flags=cv2.SOLVEPNP_ITERATIVE)使用LM优化迭代算法介绍

• flags=cv2.SOLVEPNP_ITERATIVE

3、epnp相关源码：

• epnp.h
• epnp.cpp
• solvepnp.cpp

---

• 评估计算的R和T的函数源码定义：void epnp::estimate_R_and_t(double R[3][3], double t[3])
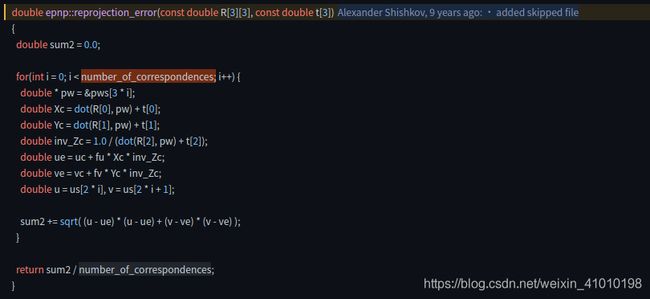
• 重投影误差函数的定义：double epnp::reprojection_error(const double R[3][3], const double t[3])

重投影误差公式：

$$reprojection\_error=\frac{1}{n}\sum _i^n\sqrt{(u-ue{)}^2+(v-ve{)}^2}$$

其中：
$$n=number\_of\_correspondences$$

解释epnp为什么至少需要3对点才可以解：https://blog.csdn.net/flyyufenfei/article/details/70440067

参考：https://blog.csdn.net/boksic/article/details/79177055
参考：https://blog.csdn.net/xueyinhualuo/article/details/46931989
参考：https://blog.csdn.net/a6333230/article/details/83304098
参考：https://blog.csdn.net/u014709760/article/details/88029841
参考：https://www.jianshu.com/p/b3e9fb2ad0dc
参考：https://zhuanlan.zhihu.com/p/58648937