数字图像处理——图像频域增强

图像频域增强

图像变换是图像频域增强技术的基础，也是变换域分析理论的基础，图像频域增强基于图像信号的频域模型。

图像变换的目的

简化图像的处理；便于图像特征的提取；图像压缩；从概念上增强对图像信息的理解。

傅里叶变换

在图像处理中，傅里叶变换一种有效而重要的方法，如：图像特征提取，频率域滤波，周期性噪声的去除，图像恢复等。可以将图像从空间域转换到频率域进行处理。

至于傅里叶变换的其他概念和具体实现细节，这里不多阐述，涉及到信号分析的知识，这篇博客主要介绍在opencv中关于频域增强的一些模块的使用。

先可以简单演示一下：

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

img = cv.imread('pictures/cat.jpg')
img = cv.cvtColor(img, cv.COLOR_BGR2GRAY)

# 傅里叶变换
f = np.fft.fft2(img)
# 将零频点移到频谱的中间
fshift = np.fft.fftshift(f)

# 取绝对值：将复数变化成实数
# 取对数的目的为了将数据变化到较小的范围（比如0-255）
# 计算振幅图
s1 = np.log(np.abs(f))
s2 = np.log(np.abs(fshift))

plt.subplot(121), plt.imshow(img, 'gray'), plt.title('orignalimg')
plt.subplot(122), plt.imshow(s2, 'gray'), plt.title('amplitude')
plt.show()

空间频率的理解

对于图像信号而言，空间频率是指单位长度内亮度(灰度)作周期性变化的次数，是图像中灰度变化剧烈程度的指标，也可以理解为灰度在平面空间上的梯度。

上面右边的图像就是频率域图像，是对原始图像作傅里叶变换得到的频谱图，频谱图和原图像上各点不存在一一对应的关系，即使在不移频的情况下也没有。图像中低频部分指低梯度的点，高频部分是梯度大的点。

从幅度谱我们可以看出明亮线和原始图像中对应的轮廓线是垂直的。如果原始图像中有圆形区域，那么幅度谱中也呈圆形分布。

若图像没有特定结构，幅度谱中比较亮一些斜线是由原图的边缘部分产生的。

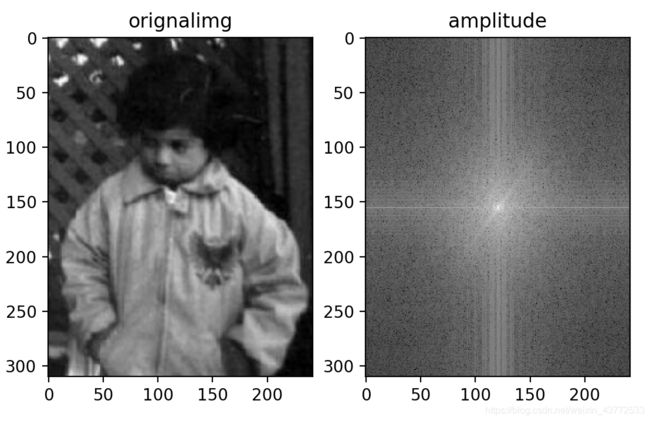
明显，频谱图中暗的点数更多，实际图像则比较柔和；反之，亮点多则图像比较尖锐。

如何看频谱图

（1）频谱图像以图像的中心为坐标原点，具有对称性。
（2）图像中心为原始图像的平均亮度，频率为0，从图像中心向外，频率增高。高亮度表明频率特征明显。
（3）频谱图像中心明显的频率变化方向与原图像中轮廓（边界）的方向垂直。也就是说如果原始图像中有多种水平分布的边界，那么频率域图像中在垂直方向的频率变化比较明显。如果原始图像中边界在左上-右上分布，那么频率域图像中在左上-右下方向频率变化明显。

从频域变回空间域

首先ifftshift将零频点移回去，然后反傅里叶变换，看看代码和生成结果。

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

img = cv.imread('pictures/cat.jpg', 0)

# 傅里叶变换
f = np.fft.fft2(img)
# 将零频点移到频谱的中间
fshift = np.fft.fftshift(f)

# 取绝对值：将复数变化成实数
# 取对数的目的为了将数据变化到较小的范围（比如0-255）
# 计算振幅图
s1 = np.log(np.abs(f))
s2 = np.log(np.abs(fshift))

plt.subplot(121), plt.imshow(img, 'gray'), plt.title('orignalimg')
plt.subplot(122), plt.imshow(s2, 'gray'), plt.title('amplitude')
plt.show()

#逆变换-幅值
f1shift = np.fft.ifftshift(fshift)
img_back = np.fft.ifft2(f1shift)
# 复数变实数
img_back = np.abs(img_back)
img_back = (img_back - np.amin(img_back)) / (np.amax(img_back) -
                                             np.amin(img_back))
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('orignalimg')
plt.subplot(122), plt.imshow(img_back, 'gray'), plt.title('imageback')
plt.show()