变分推断(variational inference)/variational EM
诸神缄默不语-个人CSDN博文目录
由于我真的,啥都不会,所以本文基本上就是,从0开始。
我看不懂的博客就是写得不行的博客。所以我只写我看得懂的部分。
持续更新。
文章目录
- 1. 琴生不等式
- 2. 香农信息量/自信息I
- 3. 信息熵
- 4. 相对熵/KL散度/信息散度
- 5. 最大似然
-
- 5.1 表述方式1
- 5.2 表述方式2
- 5.3 在有监督分类任务中的应用
- 6. EM
-
- 6.1 EM算法介绍
-
- 6.1.1 最小化KL散度视角
- 6.1.2 Evidence Lower Bound (ELBO)
- 6.2 EM算法的训练流程
-
- 6.2.1 示例1:三硬币模型
- 6.2.2 示例2:高斯混合模型GMM
- 6.3 EM算法的优点
- 7. Variational EM
- 8. 本文撰写过程中使用的其他参考资料
1. 琴生不等式
证明加权形式(令 a 1 = a 2 = ⋯ = a n = 1 n a_{1}=a_{2}=\cdots=a_{n}=\dfrac{1}{n} a1=a2=⋯=an=n1即为一般形式):
首先证明 a 1 x 1 + a 2 x 2 + ⋯ + a n x n a_1x_1+a_2x_2+\dots+a_nx_n a1x1+a2x2+⋯+anxn仍然在 [ a , b ] [a,b] [a,b]内(另一种证明思路见百度百科,即参考资料链接1):
不妨设 x 1 ≥ x 2 ≥ ⋯ ≥ x n x_1\geq x_2\geq\dots\geq x_n x1≥x2≥⋯≥xn
a 1 x 1 + a 2 x 2 + ⋯ + a n x n = a 1 ( x 1 − x 2 ) + ( a 1 + a 2 ) ( x 2 − x 3 ) + ⋯ + ( a 1 + a 2 + ⋯ + a n − 1 ) ( x n − 1 − x n ) + ( a 1 + a 2 + ⋯ + a n ) x n a_1x_1+a_2x_2+\dots+a_nx_n=a_1(x_1-x_2)+(a_1+a_2)(x_2-x_3)+\dots+(a_1+a_2+\dots+a_{n-1})(x_{n-1}-x_n)+(a_1+a_2+\dots+a_n)x_n a1x1+a2x2+⋯+anxn=a1(x1−x2)+(a1+a2)(x2−x3)+⋯+(a1+a2+⋯+an−1)(xn−1−xn)+(a1+a2+⋯+an)xn
(这个我自己想是想不出来的,但是我可以理解。大概展开是这样的:)

每一项的值都是 [ 0 , x i − x i + 1 ] [0,x_i-x_{i+1}] [0,xi−xi+1],最后一项是 x n x_n xn,所以整个多项式的取值范围是 [ x n , x 1 ] [x_n,x_1] [xn,x1](右界一般情况下能不能取到我还没琢磨明白,反正 a 1 = 1 a_1=1 a1=1时肯定可以,别的情况我还没想到),显然是在 [ a , b ] [a,b] [a,b]范围内的
用数学归纳法证明不等式:
①当 n = 1 n=1 n=1时 f ( x ) ≤ f ( x ) f(x)\leq f(x) f(x)≤f(x)显然成立
②当 n = 2 n=2 n=2时:
设 x 1 ≤ x 2 x_1\leq x_2 x1≤x2
函数曲线在 ( x 1 , f ( x 1 ) ) , ( x 2 , f ( x 2 ) ) (x_1,f(x_1)),(x_2,f(x_2)) (x1,f(x1)),(x2,f(x2))所构成的直线之下,设这条直线为 g ( x ) = m x + n g(x)=mx+n g(x)=mx+n
则 a 1 f ( x 1 ) + a 2 f ( x 2 ) = a 1 ( m x 1 + n ) + a 2 ( m x 2 + n ) = m ( a 1 x 1 + a 2 x 2 ) + n = g ( a 1 x 1 + a 2 x 2 ) a_1f(x_1)+a_2f(x_2)=a_1(mx_1+n)+a_2(mx_2+n)=m(a_1x_1+a_2x_2)+n=g(a_1x_1+a_2x_2) a1f(x1)+a2f(x2)=a1(mx1+n)+a2(mx2+n)=m(a1x1+a2x2)+n=g(a1x1+a2x2)
所以 a 1 f ( x 1 ) + a 2 f ( x 2 ) = g ( a 1 x 1 + a 2 x 2 ) ≥ f ( a 1 x 1 + a 2 x 2 ) a_1f(x_1)+a_2f(x_2)=g(a_1x_1+a_2x_2)\geq f(a_1x_1+a_2x_2) a1f(x1)+a2f(x2)=g(a1x1+a2x2)≥f(a1x1+a2x2)得证
③假设对任意 n ≥ 2 n\geq2 n≥2不等式都成立,即 f ( a 1 x 1 + a 2 x 2 + a 3 x 3 + ⋯ + a n x n ) ≤ a 1 f ( x 1 ) + a 2 f ( x 2 ) + ⋯ + a n f ( x n ) f(a_1x_1+a_2x_2+a_3x_3+\dots+a_nx_n)\leq a_1f(x_1)+a_2f(x_2)+\dots+a_nf(x_n) f(a1x1+a2x2+a3x3+⋯+anxn)≤a1f(x1)+a2f(x2)+⋯+anf(xn)
则当 n = n + 1 n=n+1 n=n+1时:
f ( a 1 x 1 + a 2 x 2 + a 3 x 1 + ⋯ + a n x n + a n + 1 x n + 1 ) = f ( ( a 1 + a 2 + ⋯ + a n ) a 1 x 1 + a 2 x 2 + a 3 x 1 + ⋯ + a n x n a 1 + a 2 + ⋯ + a n + a n + 1 x n + 1 ) ≤ ( a 1 + a 2 + ⋯ + a n ) f ( a 1 x 1 + a 2 x 2 + a 3 x 1 + ⋯ + a n x n a 1 + a 2 + ⋯ + a n ) + a n + 1 f ( x n + 1 ) = ( a 1 + a 2 + ⋯ + a n ) f ( a 1 x 1 a 1 + a 2 + ⋯ + a n + a 2 x 2 a 1 + a 2 + ⋯ + a n + ⋯ + a n x n a 1 + a 2 + ⋯ + a n ) + a n + 1 f ( x n + 1 ) ≤ ( a 1 + a 2 + ⋯ + a n ) [ a 1 f ( x 1 ) a 1 + a 2 + ⋯ + a n + a 2 f ( x 2 ) a 1 + a 2 + ⋯ + a n + ⋯ + a n f ( x n ) a 1 + a 2 + ⋯ + a n ] + a n + 1 f ( x n + 1 ) = a 1 f ( x 1 ) + a 2 f ( x 2 ) + ⋯ + a n f ( x n ) + a n + 1 f ( x n + 1 ) \begin{aligned} f(a_1x_1+a_2x_2+a_3x_1+\dots+a_nx_n+a_{n+1}x_{n+1})&=f\Big((a_1+a_2+\cdots+a_n)\frac{a_1x_1+a_2x_2+a_3x_1+\dots+a_nx_n}{a_1+a_2+\cdots+a_n}+a_{n+1}x_{n+1}\Big)\\ &\leq(a_1+a_2+\cdots+a_n)f\big(\frac{a_1x_1+a_2x_2+a_3x_1+\dots+a_nx_n}{a_1+a_2+\cdots+a_n}\big)+a_{n+1}f(x_{n+1})\\ &=(a_1+a_2+\cdots+a_n)f\big(\frac{a_1x_1}{a_1+a_2+\cdots+a_n}+\frac{a_2x_2}{a_1+a_2+\cdots+a_n}+\dots+\frac{a_nx_n}{a_1+a_2+\cdots+a_n}\big)+a_{n+1}f(x_{n+1})\\ &\leq(a_1+a_2+\cdots+a_n)\Big[\frac{a_1f(x_1)}{a_1+a_2+\cdots+a_n}+\frac{a_2f(x_2)}{a_1+a_2+\cdots+a_n}+\dots+\frac{a_nf(x_n)}{a_1+a_2+\cdots+a_n}\Big]+a_{n+1}f(x_{n+1})\\ &=a_1f(x_1)+a_2f(x_2)+\dots+a_nf(x_n)+a_{n+1}f(x_{n+1}) \end{aligned} f(a1x1+a2x2+a3x1+⋯+anxn+an+1xn+1)=f((a1+a2+⋯+an)a1+a2+⋯+ana1x1+a2x2+a3x1+⋯+anxn+an+1xn+1)≤(a1+a2+⋯+an)f(a1+a2+⋯+ana1x1+a2x2+a3x1+⋯+anxn)+an+1f(xn+1)=(a1+a2+⋯+an)f(a1+a2+⋯+ana1x1+a1+a2+⋯+ana2x2+⋯+a1+a2+⋯+ananxn)+an+1f(xn+1)≤(a1+a2+⋯+an)[a1+a2+⋯+ana1f(x1)+a1+a2+⋯+ana2f(x2)+⋯+a1+a2+⋯+ananf(xn)]+an+1f(xn+1)=a1f(x1)+a2f(x2)+⋯+anf(xn)+an+1f(xn+1)
不等式得证
2. 香农信息量/自信息I
连续型随机变量:
I ( x ) = − log 2 p ( x ) = log 2 1 p ( x ) I(x)=−\log_2p(x)=\log_2\frac{1}{p(x)} I(x)=−log2p(x)=log2p(x)1
这时香农信息量的单位为比特。(如果非连续型随机变量,则为某一具体随机事件的概率,其他的同上)
香农信息量用于刻画消除随机变量在处的不确定性所需的信息量的大小。
(本节参考香农信息量__寒潭雁影的博客-CSDN博客一文,该文中还有用数据压缩来介绍为何要这么定义,我没咋看懂,但是觉得很有意思,可供参考)
对数以e为底,单位是纳特(nat)
3. 信息熵
用期望评估整体系统的信息量:“事件香农信息量×事件概率”的累加
H ( p ) = E [ I ( x ) ] = E [ − log ( p ( x ) ) ] H(p)=E\big[I(x)\big]=E\big[-\log\big(p(x)\big)\big] H(p)=E[I(x)]=E[−log(p(x))]
信息熵公式
(对于连续型随机变量):
H ( p ) = H ( X ) = E x ∼ p ( x ) [ − log p ( x ) ] = − ∫ p ( x ) log p ( x ) d x H(p)=H(X)=E_{x∼p(x)}[−\log p(x)]=−\displaystyle\int p(x)\log p(x)dx H(p)=H(X)=Ex∼p(x)[−logp(x)]=−∫p(x)logp(x)dx
(对于离散型随机变量):
H ( p ) = H ( X ) = E x ∼ p ( x ) [ − log p ( x ) ] = − ∑ i = 1 n p ( x i ) log p ( x i ) H(p)=H(X)=E_{x∼p(x)}[−\log p(x)]=−\displaystyle\sum\limits_{i=1}^np(x_i)\log p(x_i) H(p)=H(X)=Ex∼p(x)[−logp(x)]=−i=1∑np(xi)logp(xi)
注意,我们前面在说明的时候 log \log log是以2为底的,但是一般情况下在神经网络中,默认以 e e e为底,这样算出来的香农信息量虽然不是最小的可用于完整表示事件的比特数,但对于信息熵的含义来说是区别不大的。其实只要这个底数是大于1的,都能用来表达信息熵的大小。
4. 相对熵/KL散度/信息散度
两个概率分布间差异的非对称性度量。
在信息论中,相对熵等价于两个概率分布的信息熵的差值,若其中一个概率分布为真实分布( p ( x i ) p(x_i) p(xi) ),另一个为理论(拟合)分布( q ( x i ) q(x_i) q(xi) ),则此时相对熵等于交叉熵与真实分布的信息熵之差,表示使用理论分布拟合真实分布时产生的信息损耗 。
D K L ( p ∥ q ) = ∑ i = 1 N [ p ( x i ) log p ( x i ) − p ( x i ) log q ( x i ) ] D_{KL}(p∥q)=\displaystyle\sum\limits_{i=1}^N\Big[p(x_i)\log p(x_i)−p(x_i)\log q(x_i)\Big] DKL(p∥q)=i=1∑N[p(xi)logp(xi)−p(xi)logq(xi)]
有一种理解是:信息量变成了 − log ( q ) -\log(q) −log(q),但事件概率还是原先的 p p p,所以会变成那个公式
假设理论拟合出来的事件概率分布跟真实的一模一样,那么这玩意就等于真实事件的信息熵,这一点显而易见。
假设拟合的不是特别好,那么这个玩意会比真实事件的信息熵大(这个在相对熵(KL散度)__寒潭雁影的博客-CSDN博客_kl三都一文中有证明,感觉还是比较好证的)。
也就是在理论拟合出来的事件概率分布跟真实的一模一样的时候,相对熵等于0。而拟合出来不太一样的时候,相对熵大于0。这个性质很关键,因为它正是深度学习梯度下降法需要的特性。假设神经网络拟合完美了,那么它就不再梯度下降,而不完美则因为它大于0而继续下降。
(相对熵(KL散度)__寒潭雁影的博客-CSDN博客_kl三都一文中还介绍了为什么用相对熵衍生出的交叉熵而不是均方差作为损失函数来训练神经网络,主要是关心梯度消失问题。相关的分析博文还可以参考,我只浏览过一遍还没有细看:1. 深度学习1—最简单的全连接神经网络__寒潭雁影的博客-CSDN博客_全连接神经网络实例 2. 一文弄懂神经网络中的反向传播法——BackPropagation - Charlotte77 - 博客园 3. 神经网络中w,b参数的作用(为何需要偏置b的解释)_AI_盲的博客-CSDN博客_神经元 为什么要有偏置)
交叉熵:
H q ( p ) = ∑ x p ( x ) log 1 q ( x ) H_q(p)=\sum_xp(x)\log\frac{1}{q(x)} Hq(p)=x∑p(x)logq(x)1
KL散度=交叉熵-信息熵
D K L ( p ∥ q ) = H q ( p ) − H ( p ) = ∑ x p ( x ) log 1 q ( x ) − ( − ∑ x p ( x ) log p ( x ) ) = ∑ i = 1 N [ p ( x i ) log p ( x i ) − p ( x i ) log q ( x i ) ] \begin{aligned} D_{KL}(p∥q)&=H_q(p)-H(p)\\ &=\sum_xp(x)\log\frac{1}{q(x)}-\bigg(-\sum_xp(x)\log p(x)\bigg)\\ &=\displaystyle\sum\limits_{i=1}^N\Big[p(x_i)\log p(x_i)−p(x_i)\log q(x_i)\Big] \end{aligned} DKL(p∥q)=Hq(p)−H(p)=x∑p(x)logq(x)1−(−x∑p(x)logp(x))=i=1∑N[p(xi)logp(xi)−p(xi)logq(xi)]

第一行表示p所含的信息量/平均编码长度 H ( p ) H(p) H(p);
第二行是cross-entropy,即用q来编码p所含的信息量/平均编码长度|或者称之为q对p的cross-entropy;
第三行是上面两者之间的差值,即q对p的KL距离,KL距离越大说明差值越大,说明两个分布的差异越大。
(注意这三者都是非负的。上面说的KL和cross-entropy是两个不同分布之间的距离度量,因此用 H ( p ) H(p) H(p)来表示熵。如果是测量同一分布中两个变量相互影响的关系,则一般用 H ( X ) H(X) H(X)来表示熵,如联合信息熵和条件信息熵 - 简书(我还没看))
这一部分我还没看的参考资料:1. 【机器学习】信息量,信息熵,交叉熵,KL散度和互信息(信息增益)_哈乐笑的博客-CSDN博客(这一篇公式符号似乎有问题) 2. 熵 (信息论) - 维基百科,自由的百科全书
5. 最大似然
求一组使概率(似然)最大化的参数(通过取对数后求导的方式)。
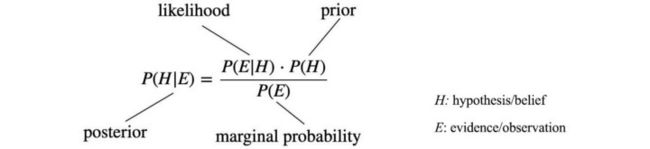
关于贝叶斯定理中不同术语的定义:
5.1 表述方式1
来自百度百科,比较清晰简单的介绍,本科统计学知识就能直观理解:


5.2 表述方式2
来自从最大似然到EM算法,不过是最小化KL散度而已 - 知乎的表述方法:

(3→4:理论上4式右半部分乘以n就可以得到3式
5→6:感觉也是比较直觉可得的)

(最小化KL散度→拟合两种分布。这里从第二行变成第三行应该是因为 p ~ ( X ) \tilde{p}(X) p~(X)可视为已知常量)
5.3 在有监督分类任务中的应用
在有监督学习模式中, ( X , Y ) (X,Y) (X,Y)就构成了一个事件:

但是我们要求的不是 ( X , Y ) (X,Y) (X,Y)的期望,而是 ( Y ∣ X ) (Y|X) (Y∣X)的,所以根据 p ( X , Y ) = p ( X ) p ( Y ∣ X ) p(X,Y)=p(X)p(Y|X) p(X,Y)=p(X)p(Y∣X),从这一步:
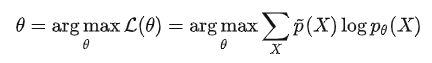
直接认为 p θ ( X ) = p ~ ( X ) p_\theta(X)=\tilde{p}(X) pθ(X)=p~(X)(事件统计概率),那么这就是个常数项:
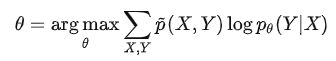
p ~ ( X , Y ) = p ~ ( X ) p ~ ( Y ∣ X ) \tilde{p}(X,Y)=\tilde{p}(X)\ \tilde{p}(Y|X) p~(X,Y)=p~(X) p~(Y∣X):

在有监督分类时, p ~ ( Y ∣ X ) \tilde{p}(Y|X) p~(Y∣X)仅在 Y = Y t Y=Y_t Y=Yt(即正确标签)时为1,其余情况都为0:
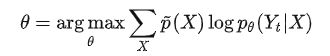
这一部分作者在评论区给出的解释是:这里的Y代表离散值,Y只有作为模型输出时才是连续的
6. EM
简而言之:是一种优化算法。
一般用于MLE(最大似然估计)问题,估计参数。
根据已知的观察结果 x x x,通过 maximum likelihood principle 导出我们觉得最合理的 model(也称为 identification) θ \theta θ。
θ ^ M L = arg max θ p ( x ; θ ) \hat{\theta}_{ML} = \underset{\theta}{\arg\!\max} \; p(\mathbf{x}; \theta) θ^ML=θargmaxp(x;θ)
一种trick就是增加隐变量 z \mathbf{z} z:
p ( x ; θ ) = ∫ p ( x , z ; θ ) d z p(\mathbf{x};\theta) = \int p(\mathbf{x}, \mathbf{z}; \theta) d\mathbf{z} p(x;θ)=∫p(x,z;θ)dz
这种问题常用stochastic sampling (Monte Carlo methods)、用一些假设来绕过计算,或用variational inference
6.1 EM算法介绍
EM算法解决含有隐变量 (hidden variable) 的概率模型参数的极大似然估计,每次迭代由两步组成:
E步, 求期望 (expectation)
M步, 使期望最大化 (maximization)
所以这一算法称为期望极大算法 (expectation maximization algorithm) ,简称EM算法。
6.1.1 最小化KL散度视角
EM算法的原理是最小化KL散度。
有监督场景下的最大似然估计:
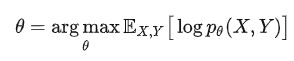
如果只给出X,那么Y就是隐变量
举例:GMM模型
![]()
不用 p θ ( X ) p θ ( Y ∣ X ) p_\theta(X)p_\theta(Y|X) pθ(X)pθ(Y∣X)是因为两项都难估计。
p ( Y ) p(Y) p(Y)易得(分类问题)
p ( X ∣ Y ) p(X|Y) p(X∣Y):这些X都属于同一类,所以应该长得差不多→假设为正态分布
只知道 X X X
Y Y Y是隐变量
( p ~ \tilde{p} p~是统计频率)(没看懂 p ~ \tilde{p} p~和 p p p的区别)
K L ( p ~ ( X , Y ) ∣ ∣ p θ ( X , Y ) ) = ∑ X , Y p ~ ( X , Y ) log p ~ ( X , Y ) p θ ( X , Y ) = ∑ X , Y p ~ ( X ) p ~ ( Y ∣ X ) log p ~ ( Y ∣ X ) p ~ ( X ) p θ ( X ∣ Y ) p θ ( Y ) = ∑ X p ~ ( X ) ∑ Y p ~ ( Y ∣ X ) log p ~ ( Y ∣ X ) p ~ ( X ) p θ ( X ∣ Y ) p θ ( Y ) = E X [ ∑ Y p ~ ( Y ∣ X ) log p ~ ( Y ∣ X ) p ~ ( X ) p θ ( X ∣ Y ) p θ ( Y ) ] = E X [ ∑ Y p ~ ( Y ∣ X ) log p ~ ( Y ∣ X ) p θ ( X ∣ Y ) p θ ( Y ) + ∑ Y p ~ ( Y ∣ X ) log p ~ ( X ) ] ( 对 数 乘 法 ) = E X [ ∑ Y p ~ ( Y ∣ X ) log p ~ ( Y ∣ X ) p θ ( X ∣ Y ) p θ ( Y ) ] + E [ log p ~ ( X ) ] \begin{aligned} &KL\big(\tilde{p}(X,Y)||p_\theta(X,Y)\big)\\ &=\sum_{X,Y}\tilde{p}(X,Y)\log\frac{\tilde{p}(X,Y)}{p_\theta(X,Y)}\\ &=\sum_{X,Y}\tilde{p}(X)\tilde{p}(Y|X)\log\frac{\tilde{p}(Y|X)\tilde{p}(X)}{p_\theta(X|Y)p_\theta(Y)}\\ &=\sum_{X}\tilde{p}(X)\sum_Y\tilde{p}(Y|X)\log\frac{\tilde{p}(Y|X)\tilde{p}(X)}{p_\theta(X|Y)p_\theta(Y)}\\ &=\mathbb{E}_X\Bigg[\sum_Y\tilde{p}(Y|X)\log\frac{\tilde{p}(Y|X)\tilde{p}(X)}{p_\theta(X|Y)p_\theta(Y)}\Bigg]\\ &=\mathbb{E}_X\Bigg[\sum_Y\tilde{p}(Y|X)\log\frac{\tilde{p}(Y|X)}{p_\theta(X|Y)p_\theta(Y)}+\sum_Y\tilde{p}(Y|X)\log\tilde{p}(X)\Bigg](对数乘法)\\ &=\mathbb{E}_X\Bigg[\sum_Y\tilde{p}(Y|X)\log\frac{\tilde{p}(Y|X)}{p_\theta(X|Y)p_\theta(Y)}\Bigg]+\mathbb{E}\big[\log\tilde{p}(X)\big] \end{aligned} KL(p~(X,Y)∣∣pθ(X,Y))=X,Y∑p~(X,Y)logpθ(X,Y)p~(X,Y)=X,Y∑p~(X)p~(Y∣X)logpθ(X∣Y)pθ(Y)p~(Y∣X)p~(X)=X∑p~(X)Y∑p~(Y∣X)logpθ(X∣Y)pθ(Y)p~(Y∣X)p~(X)=EX[Y∑p~(Y∣X)logpθ(X∣Y)pθ(Y)p~(Y∣X)p~(X)]=EX[Y∑p~(Y∣X)logpθ(X∣Y)pθ(Y)p~(Y∣X)+Y∑p~(Y∣X)logp~(X)](对数乘法)=EX[Y∑p~(Y∣X)logpθ(X∣Y)pθ(Y)p~(Y∣X)]+E[logp~(X)]
E [ log p ~ ( X ) ] \mathbb{E}\big[\log\tilde{p}(X)\big] E[logp~(X)]是常数,所以只需要优化第一项式,使 K L ( p ~ ( X , Y ) ∣ ∣ p θ ( X , Y ) ) KL\big(\tilde{p}(X,Y)||p_\theta(X,Y)\big) KL(p~(X,Y)∣∣pθ(X,Y))最小。
首先假设 p ~ ( Y ∣ X ) \tilde{p}(Y|X) p~(Y∣X)已知(在上一轮中得到):
θ ( r ) = arg min θ E X [ ∑ Y p ~ ( r − 1 ) ( Y ∣ X ) log p ~ ( r − 1 ) ( Y ∣ X ) p θ ( X ∣ Y ) p θ ( Y ) ] = arg max θ E X [ ∑ Y p ~ ( r − 1 ) ( Y ∣ X ) log p θ ( X ∣ Y ) p θ ( Y ) ] \begin{aligned} \theta^{(r)}&=\argmin_\theta\mathbb{E}_X\Bigg[\sum_Y\tilde{p}^{(r-1)}(Y|X)\log\frac{\tilde{p}^{(r-1)}(Y|X)}{p_\theta(X|Y)p_\theta(Y)}\Bigg]\\ &=\argmax_\theta\mathbb{E}_X\Bigg[\sum_Y\tilde{p}^{(r-1)}(Y|X)\log p_\theta(X|Y)p_\theta(Y)\Bigg] \end{aligned} θ(r)=θargminEX[Y∑p~(r−1)(Y∣X)logpθ(X∣Y)pθ(Y)p~(r−1)(Y∣X)]=θargmaxEX[Y∑p~(r−1)(Y∣X)logpθ(X∣Y)pθ(Y)]
得到 θ ( r ) \theta^{(r)} θ(r)后,假设 p θ ( X ∣ Y ) p_\theta(X|Y) pθ(X∣Y)已知,求 p ~ ( Y ∣ X ) \tilde{p}(Y|X) p~(Y∣X):
p ~ ( r ) ( Y ∣ X ) = arg min p ~ ( Y ∣ X ) [ ∑ Y p ~ ( Y ∣ X ) log p ~ ( Y ∣ X ) p θ ( r ) ( X ∣ Y ) p θ ( r ) ( Y ) ] \tilde{p}^{(r)}(Y|X)=\argmin_{\tilde{p}(Y|X)}\Bigg[\sum_Y\tilde{p}(Y|X)\log\frac{\tilde{p}(Y|X)}{p_\theta^{(r)}(X|Y)p_\theta^{(r)}(Y)}\Bigg] p~(r)(Y∣X)=p~(Y∣X)argmin[Y∑p~(Y∣X)logpθ(r)(X∣Y)pθ(r)(Y)p~(Y∣X)]
方括号内的部分:
∑ Y p ~ ( Y ∣ X ) log p ~ ( Y ∣ X ) p θ ( r ) ( X ∣ Y ) p θ ( r ) ( Y ) = ∑ Y p ~ ( Y ∣ X ) log p ~ ( Y ∣ X ) p θ ( r ) ( X , Y ) = ∑ Y p ~ ( Y ∣ X ) log p ~ ( Y ∣ X ) p θ ( r ) ( Y ∣ X ) p θ ( r ) ( X ) = ∑ Y p ~ ( Y ∣ X ) log [ p ~ ( Y ∣ X ) p θ ( r ) ( Y ∣ X ) − p θ ( r ) ( X ) ] = ∑ Y p ~ ( Y ∣ X ) log p ~ ( Y ∣ X ) p θ ( r ) ( Y ∣ X ) − ∑ Y p ~ ( Y ∣ X ) log p θ ( r ) ( X ) = K L ( p ~ ( Y ∣ X ) p θ ( r ) ( Y ∣ X ) ) − 常 数 ( 我 只 能 看 出 θ ( r ) 已 知 , 别 的 为 什 么 能 构 成 常 数 没 理 解 ) \begin{aligned} &\sum_Y\tilde{p}(Y|X)\log\frac{\tilde{p}(Y|X)}{p_\theta^{(r)}(X|Y)p_\theta^{(r)}(Y)}\\ &=\sum_Y\tilde{p}(Y|X)\log\frac{\tilde{p}(Y|X)}{p_\theta^{(r)}(X,Y)}\\ &=\sum_Y\tilde{p}(Y|X)\log\frac{\tilde{p}(Y|X)}{p_\theta^{(r)}(Y|X)p_\theta^{(r)}(X)}\\ &=\sum_Y\tilde{p}(Y|X)\log\Bigg[\frac{\tilde{p}(Y|X)}{p_\theta^{(r)}(Y|X)}-p_\theta^{(r)}(X)\Bigg]\\ &=\sum_Y\tilde{p}(Y|X)\log\frac{\tilde{p}(Y|X)}{p_\theta^{(r)}(Y|X)}-\sum_Y\tilde{p}(Y|X)\log p_\theta^{(r)}(X)\\ &=KL\big(\tilde{p}(Y|X)p_\theta^{(r)}(Y|X)\big)-常数\textcolor{red}{(我只能看出\theta^{(r)}已知,别的为什么能构成常数没理解)} \end{aligned} Y∑p~(Y∣X)logpθ(r)(X∣Y)pθ(r)(Y)p~(Y∣X)=Y∑p~(Y∣X)logpθ(r)(X,Y)p~(Y∣X)=Y∑p~(Y∣X)logpθ(r)(Y∣X)pθ(r)(X)p~(Y∣X)=Y∑p~(Y∣X)log[pθ(r)(Y∣X)p~(Y∣X)−pθ(r)(X)]=Y∑p~(Y∣X)logpθ(r)(Y∣X)p~(Y∣X)−Y∑p~(Y∣X)logpθ(r)(X)=KL(p~(Y∣X)pθ(r)(Y∣X))−常数(我只能看出θ(r)已知,别的为什么能构成常数没理解)
所以优化 θ ( r ) \theta^{(r)} θ(r)相当于最小化 K L ( p ~ ( Y ∣ X ) p θ ( r ) ( Y ∣ X ) ) KL\big(\tilde{p}(Y|X)p_\theta^{(r)}(Y|X)\big) KL(p~(Y∣X)pθ(r)(Y∣X))。根据KL散度的性质,最优解就是两个分布完全一致,即:
p ~ ( Y ∣ X ) = p θ ( r ) ( Y ∣ X ) = p θ ( r ) ( X ∣ Y ) p θ ( r ) ( Y ) ∑ Y p θ ( r ) ( X ∣ Y ) p θ ( r ) ( Y ) \tilde{p}(Y|X)=p_\theta^{(r)}(Y|X)=\frac{p_\theta^{(r)}(X|Y)p_\theta^{(r)}(Y)}{\sum_Yp_\theta^{(r)}(X|Y)p_\theta^{(r)}(Y)} p~(Y∣X)=pθ(r)(Y∣X)=∑Ypθ(r)(X∣Y)pθ(r)(Y)pθ(r)(X∣Y)pθ(r)(Y)
所以更新方式为:
p ~ ( Y ∣ X ) = p θ ( r ) ( X ∣ Y ) p θ ( r ) ( Y ) ∑ Y p θ ( r ) ( X ∣ Y ) p θ ( r ) ( Y ) \tilde{p}(Y|X)=\frac{p_\theta^{(r)}(X|Y)p_\theta^{(r)}(Y)}{\sum_Yp_\theta^{(r)}(X|Y)p_\theta^{(r)}(Y)} p~(Y∣X)=∑Ypθ(r)(X∣Y)pθ(r)(Y)pθ(r)(X∣Y)pθ(r)(Y)
因为我们没法一步到位求它的最小值,所以现在就将它交替地训练:先固定一部分,最大化另外一部分,然后交换过来。
回顾前文得到的:
θ ( r ) = arg max θ E X [ ∑ Y p ~ ( r − 1 ) ( Y ∣ X ) log p θ ( X ∣ Y ) p θ ( Y ) ] \theta^{(r)}\textcolor{blue}{=\argmax_\theta}\textcolor{green}{\mathbb{E}_X}\Bigg[\sum_Y\tilde{p}^{(r-1)}(Y|X)\log p_\theta(X|Y)p_\theta(Y)\Bigg] θ(r)=θargmaxEX[Y∑p~(r−1)(Y∣X)logpθ(X∣Y)pθ(Y)]
绿色部分就是E(求期望),蓝色部分就是M(求最大)
被E的式子就是Q函数
6.1.2 Evidence Lower Bound (ELBO)
设 q ( z ) q(z) q(z)是 z z z上的概率分布
ln p ( x ; θ ) = ∫ q ( z ) ln p ( x ; θ ) d z = ∫ q ( z ) ln ( p ( x ; θ ) p ( z ∣ x ; θ ) p ( z ∣ x ; θ ) ) d z = ∫ q ( z ) ln ( p ( x , z ; θ ) p ( z ∣ x ; θ ) ) d z = ∫ q ( z ) ln ( p ( x , z ; θ ) q ( z ) p ( z ∣ x ; θ ) q ( z ) ) d z = ∫ q ( z ) ln ( p ( x , z ; θ ) q ( z ) ) d z − ∫ q ( z ) ln ( p ( z ∣ x ; θ ) q ( z ) ) d z = F ( q , θ ) + K L ( q ∣ ∣ p ) \begin{aligned} \ln p(x; \theta) & = \int q(z) \ln p(x; \theta) dz \\ & = \int q(z) \ln \Big( \frac{p(x; \theta) p(z | x; \theta)}{p(z | x; \theta)} \Big) dz \\ & = \int q(z) \ln \Big( \frac{p(x, z; \theta)}{p(z | x; \theta)} \Big) dz \\ & = \int q(z) \ln \Big( \frac{p(x, z; \theta) q(z)}{p(z | x; \theta) q(z)} \Big) dz \\ & = \int q(z) \ln \Big( \frac{p(x, z; \theta)}{q(z)} \Big) dz - \int q(z) \ln \Big( \frac{p(z | x; \theta)}{q(z)} \Big) dz \\ & = F(q, \theta) + KL(q || p) \end{aligned} lnp(x;θ)=∫q(z)lnp(x;θ)dz=∫q(z)ln(p(z∣x;θ)p(x;θ)p(z∣x;θ))dz=∫q(z)ln(p(z∣x;θ)p(x,z;θ))dz=∫q(z)ln(p(z∣x;θ)q(z)p(x,z;θ)q(z))dz=∫q(z)ln(q(z)p(x,z;θ))dz−∫q(z)ln(q(z)p(z∣x;θ))dz=F(q,θ)+KL(q∣∣p)
F ( q , θ ) F(q, \theta) F(q,θ)就是evidence lower bound (ELBO)或the negative of the variational free energy
因为KL散度是非负的,所以 ln p ( x ; θ ) ≥ F ( q , θ ) \ln p(x; \theta) \ge F(q, \theta) lnp(x;θ)≥F(q,θ),所以ELBO给marginal likelihood提供了下限。所以Expectation Maximization (EM)和variational inference最大化variational lower bound,而不直接最大化marginal likelihood
假设我们能analytically得到 p ( z ∣ x ; θ O L D ) p(z | x; \theta^{OLD}) p(z∣x;θOLD)(对高斯混合模型来说就是softmax),那我们就能 q ( z ) = p ( z ∣ x ; θ O L D ) q(z) = p(z | x; \theta^{OLD}) q(z)=p(z∣x;θOLD)
F ( q , θ ) = ∫ q ( z ) ln ( p ( x , z ; θ ) q ( z ) ) d z = ∫ q ( z ) ln p ( x , z ; θ ) d z − ∫ q ( z ) ln q ( z ) d z = ∫ p ( z ∣ x ; θ O L D ) ln p ( x , z ; θ ) d z − ∫ p ( z ∣ x ; θ O L D ) ln p ( z ∣ x ; θ O L D ) d z = Q ( θ , θ O L D ) + H ( q ) \begin{aligned} F(q, \theta) & = \int q(z) \ln \Big( \frac{p(x, z; \theta)}{q(z)} \Big) dz \\ & = \int q(z) \ln p(x, z; \theta) dz - \int q(z) \ln q(z) dz \\ & = \int p(z | x; \theta^{OLD}) \ln p(x, z; \theta) dz \\ & \quad - \int p(z | x; \theta^{OLD}) \ln p(z | x; \theta^{OLD}) dz \\ & = Q(\theta, \theta^{OLD}) + H(q) \end{aligned} F(q,θ)=∫q(z)ln(q(z)p(x,z;θ))dz=∫q(z)lnp(x,z;θ)dz−∫q(z)lnq(z)dz=∫p(z∣x;θOLD)lnp(x,z;θ)dz−∫p(z∣x;θOLD)lnp(z∣x;θOLD)dz=Q(θ,θOLD)+H(q)
第二项 H ( z ∣ x ) H(z|x) H(z∣x)是给定x条件下z的熵,是 θ O L D \theta^{OLD} θOLD的函数, θ O L D \theta^{OLD} θOLD当成已知项,所以这项是常数
EM算法的目标就是 arg max θ Q ( θ , θ O L D ) \argmax\limits_\theta Q(\theta, \theta^{OLD}) θargmaxQ(θ,θOLD)
(Gibbs entropy)
- E:计算 p ( z ∣ x ; θ O L D ) p(z | x; \theta^{OLD}) p(z∣x;θOLD)
- M:计算 arg max θ ∫ p ( z ∣ x ; θ O L D ) ln p ( x , z ; θ ) d z \argmax\limits_\theta\displaystyle\int p(z | x; \theta^{OLD}) \ln p(x, z; \theta) dz θargmax∫p(z∣x;θOLD)lnp(x,z;θ)dz
For example, the EM for the Gaussian Mixture Model consists of an expectation step where you compute the soft assignment of each datum to K clusters, and a maximization step which computes the parameters of each cluster using the assignment. However, for complex models, we cannot use the EM algorithm.
另一种推导出ELBO的方法,利用琴生不等式(函数是 log x \log x logx):

6.2 EM算法的训练流程
使用KL散度作为联合分布的差异性度量,然后对KL散度交替最小化
输入:观测变量数据X,隐变量数据Y,联合分布 p θ ( X , Y ) p_\theta(X,Y) pθ(X,Y),条件分布 p θ ( Y ∣ X ) p_\theta(Y|X) pθ(Y∣X)(总之是指含有未知数 θ \theta θ的式子)
输出:模型参数 θ \theta θ
我的理解:
- 先确定X,Y,θ
- 给出Q关于θ的表达式
- 重复步骤:代入θ计算E(Q),计算使E极大的θ
(EM算法的收敛性证明略)
6.2.1 示例1:三硬币模型

Step1:观测变量是掷硬币的结果,隐变量是使用哪一枚硬币,而模型参数是硬币的出现正面的概率。
重复以上计算, 直到对数似然函数值不再有明显的变化为止。
代码实现:
import numpy as np
import math
def em_single(theta,Y):
"""每一轮EM算法"""
u_group=[] #Y_i:丢的是第一枚硬币的概率
pi=theta[0]
p=theta[1]
q=theta[2]
#E:通过计算E得到隐变量
for y in Y:
u=(pi*math.pow(p,y)*math.pow(1-p,1-y))/(pi*math.pow(p,y)*math.pow(1-p,1-y)+(1-pi)*math.pow(q,y)*math.pow(1-q,1-y))
u_group.append(u)
#M:计算使Q极大化的参数
new_pi=sum(u_group)/len(Y)
new_p=sum(u_group[i]*Y[i] for i in range(len(Y)))/sum(u_group)
new_q=sum((1-u_group[i])*Y[i] for i in range(len(Y)))/sum(1-u_group[i] for i in range(len(Y)))
return [new_pi,new_p,new_q]
def threecoins(theta,Y):
j=0 #步数
while j<1000:
new_theta=em_single(theta,Y)
if new_theta==theta: #收敛(这里设置一个阈值可能会更好)
break
else:
theta = new_theta
j=j+1
print(new_theta)
return new_theta
if __name__=="__main__":
Y = [1, 1, 0, 1, 0, 0, 1, 0, 1, 1] #其实这里写成X可能会更好
theta=[0.4,0.6,0.7] #初始参数
result=threecoins(theta,Y)
print("模型参数的极大似然估计是",result)
6.2.2 示例2:高斯混合模型GMM

图中正确的似乎应该是 θ k = ( μ k , σ k ) \theta_k=(\mu_k,\sigma_k) θk=(μk,σk)
GMM就是一堆高斯模型按概率随机选择一个生成观测值。

p ( x i ∣ z i = k ) ∼ N ( μ k , σ k ) p(x_i | z_i=k) \sim \mathcal{N}(\mu_k, \sigma_k) p(xi∣zi=k)∼N(μk,σk)
明确隐变量和对数似然函数:



代码实现:
做2个高斯分布混合,长度为1000
import numpy as np
import random
import math
import time
def loadData(mu0, sigma0, mu1, sigma1, alpha0, alpha1):
'''
初始化数据集
这里通过服从高斯分布的随机函数来伪造数据集
:param mu0: 高斯0的均值
:param sigma0: 高斯0的方差
:param mu1: 高斯1的均值
:param sigma1: 高斯1的方差
:param alpha0: 高斯0的系数
:param alpha1: 高斯1的系数
:return: 混合了两个高斯分布的数据
'''
# 定义数据集长度为1000
length = 1000
# 初始化第一个高斯分布,生成数据,数据长度为length * alpha系数,以此来
# 满足alpha的作用
data0 = np.random.normal(mu0, sigma0, int(length * alpha0))
# 第二个高斯分布的数据
data1 = np.random.normal(mu1, sigma1, int(length * alpha1))
#(其实这里可能有bug,就是这两个加起来可能不等于length。但是1000的话没这个问题,所以无所谓)
# 初始化总数据集
# 两个高斯分布的数据混合后会放在该数据集中返回
dataSet = []
# 将第一个数据集的内容添加进去
dataSet.extend(data0)
# 添加第二个数据集的数据
dataSet.extend(data1)
# 对总的数据集进行打乱(其实不打乱也没事,只不过打乱一下直观上让人感觉已经混合了
# 读者可以将下面这句话屏蔽以后看看效果是否有差别)
#(与顺序无关嘛,无所谓的)
random.shuffle(dataSet)
#返回伪造好的数据集
return dataSet
def calcGauss(dataSetArr, mu, sigmod):
'''
根据高斯密度函数计算值
注:在公式中y是一个实数,但是在EM算法中(见算法9.2的E步),需要对每个j
都求一次yjk,在本实例中有1000个可观测数据,因此需要计算1000次。考虑到
在E步时进行1000次高斯计算,程序上比较不简洁,因此这里的y是向量,在numpy
的exp中如果exp内部值为向量,则对向量中每个值进行exp,输出仍是向量的形式。
所以使用向量的形式1次计算即可将所有计算结果得出,程序上较为简洁
:param dataSetArr: 可观测数据集
:param mu: 均值
:param sigmod: 方差
:return: 整个可观测数据集的高斯分布密度(向量形式)
'''
result = (1 / (math.sqrt(2*math.pi)*sigmod)) * np.exp(-1 * (dataSetArr-mu) * (dataSetArr-mu) / (2*sigmod**2))
# 返回结果
return result
def E_step(dataSetArr, alpha0, mu0, sigmod0, alpha1, mu1, sigmod1):
'''
EM算法中的E步
依据当前模型参数,计算分模型k对观数据y的响应度
:param dataSetArr: 可观测数据y
:param alpha0: 高斯模型0的系数
:param mu0: 高斯模型0的均值
:param sigmod0: 高斯模型0的方差
:param alpha1: 高斯模型1的系数
:param mu1: 高斯模型1的均值
:param sigmod1: 高斯模型1的方差
:return: 两个模型各自的响应度
'''
# 计算y0的响应度
# 先计算模型0的响应度的分子
gamma0 = alpha0 * calcGauss(dataSetArr, mu0, sigmod0)
# 模型1响应度的分子
gamma1 = alpha1 * calcGauss(dataSetArr, mu1, sigmod1)
# 两者相加为E步中的分布
sum = gamma0 + gamma1
# 各自相除,得到两个模型的响应度
gamma0 = gamma0 / sum
gamma1 = gamma1 / sum
# 返回两个模型响应度
return gamma0, gamma1
def M_step(muo, mu1, gamma0, gamma1, dataSetArr):
mu0_new = np.dot(gamma0, dataSetArr) / np.sum(gamma0)
mu1_new = np.dot(gamma1, dataSetArr) / np.sum(gamma1)
sigmod0_new = math.sqrt(np.dot(gamma0, (dataSetArr - muo)**2) / np.sum(gamma0))
sigmod1_new = math.sqrt(np.dot(gamma1, (dataSetArr - mu1)**2) / np.sum(gamma1))
alpha0_new = np.sum(gamma0) / len(gamma0)
alpha1_new = np.sum(gamma1) / len(gamma1)
# 将更新的值返回
return mu0_new, mu1_new, sigmod0_new, sigmod1_new, alpha0_new, alpha1_new
def EM_Train(dataSetList, iter=500):
'''
根据EM算法进行参数估计
:param dataSetList:数据集(可观测数据)
:param iter: 迭代次数
:return: 估计的参数
'''
# 将可观测数据y转换为数组形式,主要是为了方便后续运算
dataSetArr = np.array(dataSetList)
# 步骤1:对参数取初值,开始迭代
alpha0 = 0.5
mu0 = 0
sigmod0 = 1
alpha1 = 0.5
mu1 = 1
sigmod1 = 1
# 开始迭代
step = 0
while (step < iter):
# 每次进入一次迭代后迭代次数加1
step += 1
# 步骤2:E步:依据当前模型参数,计算分模型k对观测数据y的响应度
gamma0, gamma1 = E_step(dataSetArr, alpha0, mu0, sigmod0, alpha1, mu1, sigmod1)
# 步骤3:M步
mu0, mu1, sigmod0, sigmod1, alpha0, alpha1 = M_step(mu0, mu1, gamma0, gamma1, dataSetArr)
# 迭代结束后将更新后的各参数返回
return alpha0, mu0, sigmod0, alpha1, mu1, sigmod1
if __name__ == '__main__':
start = time.time()
# alpha是高斯混合模型的权重α
# mu0是均值μ
# sigmod是方差σ
# 在设置上两个alpha的和必须为1,其他没有什么具体要求,符合高斯定义就可以
alpha0 = 0.3 # 系数α
mu0 = -2 # 均值μ
sigmod0 = 0.5 # 方差σ
alpha1 = 0.7 # 系数α
mu1 = 0.5 # 均值μ
sigmod1 = 1 # 方差σ
# 初始化数据集
dataSetList = loadData(mu0, sigmod0, mu1, sigmod1, alpha0, alpha1)
print('---------------------------')
print(dataSetList[:5])
#打印设置的参数
print('---------------------------')
print('the Parameters set is:')
print('alpha0:%.1f, mu0:%.1f, sigmod0:%.1f, alpha1:%.1f, mu1:%.1f, sigmod1:%.1f' % (
alpha0, alpha1, mu0, mu1, sigmod0, sigmod1
))
# 开始EM算法,进行参数估计
alpha0, mu0, sigmod0, alpha1, mu1, sigmod1 = EM_Train(dataSetList)
# 打印参数预测结果
print('----------------------------')
print('the Parameters predict is:')
print('alpha0:%.1f, mu0:%.1f, sigmod0:%.1f, alpha1:%.1f, mu1:%.1f, sigmod1:%.1f' % (
alpha0, alpha1, mu0, mu1, sigmod0, sigmod1
))
# 打印时间
print('----------------------------')
print('time span:', time.time() - start)
运行结果:
[-2.79992449645255, -2.5326809939296915, -1.8697714052358605, 0.9248711228254336, -2.2669313768298]
---------------------------
the Parameters set is:
alpha0:0.3, mu0:0.7, sigmod0:-2.0, alpha1:0.5, mu1:0.5, sigmod1:1.0
----------------------------
the Parameters predict is:
alpha0:0.3, mu0:0.7, sigmod0:-2.0, alpha1:0.5, mu1:0.5, sigmod1:1.0
----------------------------
time span: 0.06270933151245117
6.3 EM算法的优点
用EM而不用generic optimizer是因为:
- EM为某些情况下的求解提供了更好的收敛性(这一点我还没寻摸明白)
- 同时通过 latent variable 也能更好的解释一个 model,比如常见的 mixture model 等。
- The variational EM gives us a way to bypass computing the partition function and allows us to infer the parameters of a complex model using a deterministic optimization step.
7. Variational EM
对于复杂情况,我们用更简单的模型估计posterior probability。
如给定 x x x,我们假设有些隐变量独立于其他隐变量。
Such independence reduces complexity and allows us to deduce the analytic form of the EM.
还可以给定更强的,给定 x x x,所有隐变量互相独立的假设: z i ⊥ z j f o r i ≠ j z_i\perp z_j\ for\ i \neq j zi⊥zj for i=j(mean field approximation)
这样我们就可以独立更新每个隐变量的规则。
q ( z ) = ∏ i q ( z i ) q(z) = \prod_i q(z_i) q(z)=∏iq(zi),将ELBO分解为 z j z_j zj和其他隐变量:
F ( q , θ ) = ∫ q ( z ) ln ( p ( x , z ; θ ) q ( z ) ) d z = ∫ ∏ i q ( z i ) ln p ( x , z ; θ ) d z − ∑ i ∫ q ( z i ) ln q ( z i ) d z i = ∫ q ( z j ) ∫ ( ∏ i ≠ j q ( z i ) ln p ( x , z ; θ ) ) ∏ i ≠ j d z i d z j − ∫ q ( z j ) ln q ( z j ) d z j − ∑ i ≠ j ∫ q ( z i ) ln q ( z i ) d z i = ∫ q ( z j ) ln ( exp ( ⟨ ln p ( x , z ; θ ) ⟩ i ≠ j ) q ( z j ) ) d z j − ∑ i ≠ j ∫ q ( z i ) ln q ( z i ) d z i = ∫ q ( z j ) ln ( p ~ i ≠ j q ( z j ) ) d z j + H ( z i ≠ j ) + c = − K L ( q j ∣ ∣ p ~ i ≠ j ) + H ( z i ≠ j ) + c \begin{aligned} F(q, \theta) & = \int q(z) \ln \Big( \frac{p(x, z; \theta)}{q(z)} \Big) dz \\ & = \int \prod_i q(z_i) \ln p(x, z; \theta) dz - \sum_i \int q(z_i) \ln q(z_i) dz_i \\ & = \int q(z_j) \int \Big( \prod_{i \neq j} q(z_i) \ln p(x, z; \theta) \Big) \prod_{i \neq j} dz_i dz_j \\ & \quad - \int q(z_j) \ln q(z_j) dz_j - \sum_{i \neq j} \int q(z_i) \ln q(z_i) dz_i \\ & = \int q(z_j) \ln \Big( \frac{\exp(\langle \ln p(x, z; \theta)\rangle_{i \neq j})}{q(z_j)} \Big) dz_j \\ & \quad - \sum_{i \neq j} \int q(z_i) \ln q(z_i) dz_i \\ & = \int q(z_j) \ln \Big( \frac{\tilde{p}_{i\neq j}}{q(z_j)} \Big) dz_j + H(z_{i\neq j}) + c\\ & = - KL(q_j || \tilde{p}_{i\neq j}) + H(z_{i\neq j}) + c \end{aligned} F(q,θ)=∫q(z)ln(q(z)p(x,z;θ))dz=∫i∏q(zi)lnp(x,z;θ)dz−i∑∫q(zi)lnq(zi)dzi=∫q(zj)∫(i=j∏q(zi)lnp(x,z;θ))i=j∏dzidzj−∫q(zj)lnq(zj)dzj−i=j∑∫q(zi)lnq(zi)dzi=∫q(zj)ln(q(zj)exp(⟨lnp(x,z;θ)⟩i=j))dzj−i=j∑∫q(zi)lnq(zi)dzi=∫q(zj)ln(q(zj)p~i=j)dzj+H(zi=j)+c=−KL(qj∣∣p~i=j)+H(zi=j)+c

8. 本文撰写过程中使用的其他参考资料
- List of mathematic operators - Wikipedia
- 算子 - 维基百科,自由的百科全书
- 琴生不等式_百度百科
- 琴生不等式的证明_weixin_41170664的博客-CSDN博客_琴生不等式(不等式证明部分主要参考这一篇和上一篇)
- 琴生不等式 - 维基百科,自由的百科全书:这个里面的表达方式太数学了,我没看懂
- 信息熵__寒潭雁影的博客-CSDN博客_连续随机变量信息熵
- 相对熵(KL散度)__寒潭雁影的博客-CSDN博客_kl三都
- [中字]信息熵,交叉熵,KL散度介绍||机器学习的信息论基础_哔哩哔哩_bilibili:这个视频讲得很好,讲了香农信息量、信息熵、交叉熵(熵+KL散度)公式的来历和算法
- 信息熵和KL散度 - 简书
- Machine Learning — Fundamental. “One learning algorithm” hypothesizes… | by Jonathan Hui | Medium:这一篇内容相当全面。大多我只略览,没有涵盖到本博文中。有些没看懂,以后慢慢看。
内容包括:
信息论(香农信息量、熵、交叉熵、KL散度、条件熵、信息增益/互信息)
概率(概率质量函数、概率密度函数PDF、累积分布函数CDF、条件概率、独立、边缘概率、链式法则、贝叶斯定理、概率模型、非概率模型、最大似然估计MLE、最大后验估计MAPE、贝叶斯推断、点估计、偏差、方差、独立同分布i.i.d.、协变量偏移)
分布(期望、方差、协方差、样本方差、相关系数、高斯分布/正态分布、标准正态分布、多元高斯分布、中心极限定理、伯努利分布、二项分布、分类分布、多项式分布、贝塔分布、狄利克雷分布、Symmetric Dirichlet distribution、泊松分布、指数分布、拉普拉斯分布、伽马分布、卡方分布、狄拉克分布、学生T分布、归一化因子、指数族分布、K阶矩、矩匹配、频率学派、贝叶斯学派(posterior会变成prior……这样的循环)、正则化共轭先验)
导数(雅克比矩阵、海森矩阵)
矩阵分解(成分分析、奇异值分解SVD、主成分分析PCA、Probabilistic PCA、核PCA、乔莱斯基分解法、摩尔-彭若斯广义逆)
统计显著性(零假设、备择假设、P值、Z检验、置信区间、费雪精确检验、卡方检验、探索性数据分析EDA)
概率抽样(简单随机抽样、分层随机抽样、组群随机抽样、系统随机抽样)
模型评估指标(accuracy、precision、recall/sensitivity/TPR、specificity/TNR、F1 score、FPR、miss rate/FNR、prevalence、misclassification rate、ROC曲线、R方(我看到还有一种翻译叫拟合度)
范数
相似度(Jaccard Similarity、余弦相似度、皮尔森相似度) - Machine Learning — Algorithms. In the last article, we look into the… | by Jonathan Hui | Medium:这篇文章是上一篇文章的后续,介绍了一些传统机器学习方法。其中介绍了用EM算法解决MLE问题的部分,对其解读是将参数拆成两部分,分别固定其中一部分、更新另一部分。
- Machine Learning — Proof & Terms. Terms | by Jonathan Hui | Medium:这篇与上两篇文章也是同作者,这里面讲了用EM算法填补缺失值和求解GMM、PCA。具体的没看,反正有这么回事儿
- 最大似然估计_百度百科:只使用了一部分内容
- 从最大似然到EM算法,不过是最小化KL散度而已 - 知乎:这一篇讲得很好
- Statistical inference - Wikipedia:这个概念感觉比较大,这篇我还没看
- 边际似然函数(贝叶斯统计背景下)_Codefmeister的博客-CSDN博客_边际似然
- 负对数似然(negative log-likelihood)_不一样的雅兰酱的博客-CSDN博客_负对数似然函数
- Expectation Maximization and Variational Inference (Part 1):这一篇开头还能看得懂,等到说 H ( z ∣ x ) H(z|x) H(z∣x)对 θ \theta θ是常数这里之后就看不懂了。然后我就把原话搬过来了
- Expectation Maximization and Variational Inference (Part 2):用GMM举了个variational EM的例子,这篇实在是看你妈不懂
- Variational Inference for Dirichlet Process Mixtures:应该就是上一篇文章例子的出处。哎但是这个我真的看求不懂,我躺了。(这个网页好难打开,我隔了一天才打开)
- 一文让你完全入门EM算法:这篇写得还可以,以后补一下
- 谈谈Variational inference和EM算法之间的关系 - 知乎:这一篇开头的annotation写得我看不懂啊……后面的内容也有一些整合到了本博文中,但是未完全看懂,日后有机会还可以继续多看看。另外就是这一篇用期望值来定义琴生不等式,这个跟我在博文里现在写的不一样,以后可以加上用这种定义的
- cs229-notes8.dvi:是上一篇文章的重要参考资料之一,感觉写得比上一篇更清晰简明,而且内容很全面,从琴生不等式到变分推断都有。但是还没仔细看,决定以后把这里的内容再好好看看,加到博文里。(还是有些数学公式没看懂是咋推出来的)
这个是cs229课程的notes,等我以后有时间了,我也要去看cs229! - Machine Learning — Variational Inference | by Jonathan Hui | Medium:这篇对我来说有点难了,而且不知道为什么我只能看到文字,无法显示图片。所以留待以后再看吧
- Evidence Lower BOund (ELBO) - 知乎:这篇给出了琴生不等式和KL散度两种推导出ELBO的算法,都已经整合到本博文里了
- (以下部分的内容还没有仔细看)
- https://www.cs.princeton.edu/courses/archive/fall11/cos597C/lectures/variational-inference-i.pdf
- 从最大似然到EM算法:一致的理解方式 - 科学空间|Scientific Spaces
- 基于近似计算解决推断问题——变分推断(一) - 简书
- Maximum Likelihood from Incomplete Data via the EM Algorithm
- PRML
- The Elements of Statistical Learning
- EM算法之KL散度和Jensen不等式 - 知乎:没看懂
- EM算法总结:从 ELBO + KL散度出发 - 知乎:没怎么看懂,而且图画得真丑
- variational EM – demonstrate 的 blog:从凑熵那一步开始看不懂
- 变分推断(Variational Inference) | 变分:没看懂这哪儿来的 q ( z ) q(z) q(z)啊?
- D. G. Tzikas, A. C. Likas, and N. P. Galatsanos, The Variational Approximation for Bayesian Inference, IEEE Signal Processing Magazine, Nov 2008
- R.M. Neal and G.E. Hinton, A view of the EM algorithm that justifies incremental, sparse and other variants, Learning in Graphical Models, 1998
- Variational Methods
- David M Blei, Alp Kucukelbir, and Jon D McAuliffe. Variational inference: A review for statisticians. Journal of the American Statistical
Association, 112(518):859–877, 2017.
[2] Diederik P Kingma and Max Welling. Auto-encoding variational bayes.
arXiv preprint arXiv:1312.6114, 2013.