多层感知机(MLP)
多层感知机(MLP)
【代码】
以多层感知机为例,介绍多层神经网络。
1. 隐藏层
多层感知机在单层神经网络的基础上引入了一到多个隐藏层(hidden layer)。隐藏层位于输入层和输出层之间。
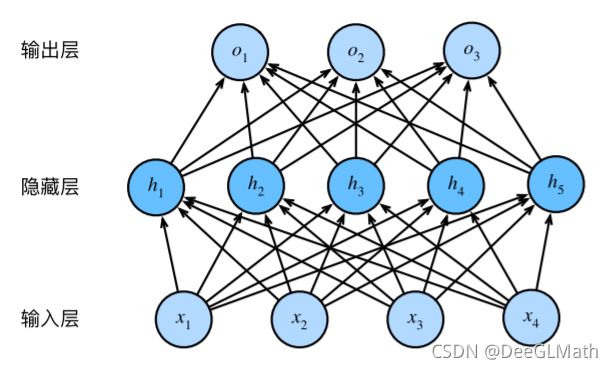
在上图的多层感知机中,输入和输出个数分别为4和3,中间的隐藏层中包含了5个隐藏单元(hidden unit)。由于输入层不涉及计算,上图中的多层感知机的层数为2.由上图可见,隐藏层中的神经元和输入层中各个输入完全连接,输出层中的神经元和隐藏层中的各个神经元也完全连接。因此,多层感知机中的隐藏层和输出层都是全连接层。
给定一个小批量样本 X ∈ R n × d X \in R^{n \times d} X∈Rn×d,其批量大小为 n n n,输入个数为 d d d。假设多层感知机只有一个隐藏层,其中隐藏单元个数为 h h h。记隐藏层的输出为 H H H,有 H ∈ R n × h H \in R^{n \times h} H∈Rn×h。因为隐藏层和输出层均是全连接层,可以设隐藏层的权重参数和偏差参数分别为:
W h ∈ R d × h , b h ∈ R 1 × h (1) W_h \in R^{d \times h}, b_h \in R^{1 \times h} \tag 1 Wh∈Rd×h,bh∈R1×h(1)
输出层的权重参数和偏差参数分别为:
W o ∈ R h × q , b o ∈ R 1 × q (2) W_o \in R^{h \times q}, b_o \in R^{1 \times q} \tag 2 Wo∈Rh×q,bo∈R1×q(2)
⼀种含单隐藏层的多层感知机的设计。其输出 O ∈ R n × q O \in R^{n \times q} O∈Rn×q的计算为:
H = X W h + b h , O = H W o + b o (3) H=XW_h+b_h, \\ O=HW_o+b_o \tag 3 H=XWh+bh,O=HWo+bo(3)
将隐藏层的输出直接作为输出层的输⼊。如果将以上两个式⼦联⽴起来,可以得到:
O = ( X W h + b h ) W o + b o = X W h W o + b h W o + b o (4) O=(XW_h+b_h)W_o+b_o=XW_hW_o+b_hW_o+b_o \tag 4 O=(XWh+bh)Wo+bo=XWhWo+bhWo+bo(4)
从联立后的式子可以看出,虽然神经网络引入了隐藏层,却依然等价于一个单层神经网络:其中输出层权重参数为 W h W o W_hW_o WhWo,偏差参数为 b h W o + b o b_hW_o+b_o bhWo+bo。所以,即便添加更多的隐藏层,以上的设计只能与仅含输出层的单层神经网络等价。
2. 激活函数
引入隐藏层的神经网络可以等价于仅含输出层的单层神经网络的问题,在于全连接层只是对数据做仿射变换(affine transformation),而多个仿射变换的叠加仍然是⼀个仿射变换。解决问题的⽅法之一是引⼊⾮线性变换,对隐藏变量使⽤按元素运算的⾮线性函数进⾏变换,再作为下⼀个全连接层的输⼊。⾮线性函数被称为激活函数(activation function)。
ReLU函数
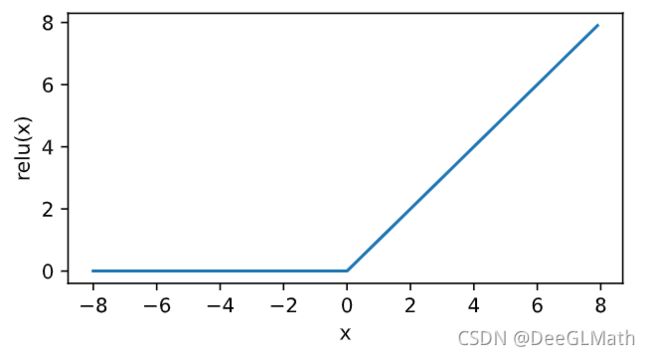
ReLU(rectified linear unit)函数提供了⼀个很简单的⾮线性变换。给定元素 x x x,该函数定义为:
R e L U ( x ) = max ( x , 0 ) (5) ReLU(x)=\max(x,0) \tag 5 ReLU(x)=max(x,0)(5)
可以看出,ReLU函数只保留正数元素,并将负数元素清零。
%matplotlib inline
from utils import set_figsize, plt
from mxnet import autograd, nd
# 定义⼀个绘图函数 xyplot
def xyplot(x_vals, y_vals, name):
set_figsize(figsize=(5, 2.5))
plt.plot(x_vals.asnumpy(), y_vals.asnumpy())
plt.xlabel('x')
plt.ylabel(name + '(x)')
# 通过 NDArray提供的 relu函数来绘制 ReLU函数
x = nd.arange(-8.0, 8.0, 0.1)
x.attach_grad() # 申请存储梯度所需的内存
with autograd.record():
y = x.relu()
xyplot(x, y, 'relu') # 该激活函数是⼀个两段线性函数
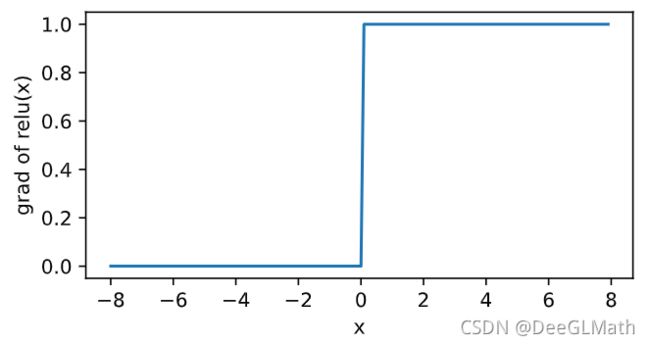
# 当输⼊为负数时,ReLU函数的导数为0;当输⼊为正数时,ReLU函数的导数为1。
y.backward() # 调用 backward函数自动求梯度
xyplot(x, x.grad, 'grad of relu')
sigmoid函数
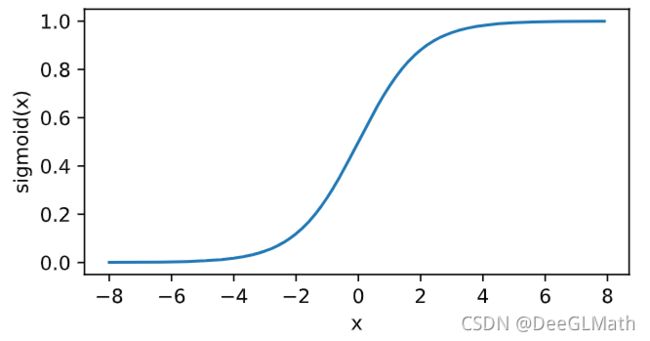
sigmoid函数可以将元素的值变换到0和1之间:
s i g m o i d ( x ) = 1 1 + exp ( − x ) (6) sigmoid(x)=\frac{1}{1+\exp(-x)} \tag 6 sigmoid(x)=1+exp(−x)1(6)
当输⼊接近0时,sigmoid函数接近线性变换。
with autograd.record():
y = x.sigmoid()
xyplot(x, y, 'sigmoid')
依据链式法则,sigmoid函数的导数:
s i g m o i d ′ ( x ) = s i g m o i d ( x ) ( 1 − s i g m o i d ( x ) ) (7) sigmoid^{'}(x)=sigmoid(x)(1-sigmoid(x)) \tag 7 sigmoid′(x)=sigmoid(x)(1−sigmoid(x))(7)
当输⼊为0时,sigmoid函数的导数达到最⼤值0.25;当输⼊越偏离0时,sigmoid函数的导数越接近0。
y.backward()
xyplot(x, x.grad, 'grad of sigmoid')
tanh函数
tanh(双曲正切)函数可以将元素的值变换到-1和1之间:
t a n h ( x ) = 1 − exp ( − 2 x ) 1 + exp ( − 2 x ) (8) tanh(x)=\frac{1-\exp(-2x)}{1+\exp(-2x)} \tag 8 tanh(x)=1+exp(−2x)1−exp(−2x)(8)
当输⼊接近0时,tanh函数接近线性变换。虽然该函数的形状和sigmoid函数的形状很像,但tanh函数在坐标系的原点上对称。
with autograd.record():
y = x.tanh()
xyplot(x, y, 'tanh')
依据链式法则,tanh函数的导数:
t a n h ′ ( x ) = 1 − t a n h 2 ( x ) (9) tanh^{'}(x)=1-tanh^2(x) \tag 9 tanh′(x)=1−tanh2(x)(9)
当输⼊为0时,tanh函数的导数达到最⼤值1;当输⼊越偏离0时,tanh函数的导数越接近0。
y.backward()
xyplot(x, x.grad, 'grad of tanh')
多层感知机就是含有⾄少⼀个隐藏层的由全连接层组成的神经⽹络,且每个隐藏层的输出通过激活函数进⾏变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。多层感知机按以下方式计算输出:
H = ϕ ( X W h + b h ) , O = H W o + b o (10) H=\phi(XW_h+b_h), \\ O=HW_o+b_o \tag {10} H=ϕ(XWh+bh),O=HWo+bo(10)
其中 ϕ \phi ϕ表⽰激活函数。