C语言解决背包问题(动态规划)、最短路径问题(dijkstra算法、floyd算法)

C语言解决背包问题、最短路径问题

  背包问题、最短路径问题是数学建模中常见的最优规划问题，已经有很成熟的解决方法。本文提供了解决这两个问题的参考资料和实现代码，回答了：①背包问题的最大价值和最优选择方案；②最短路问题的最短距离和最短路线。

1. 背包问题

1.1 基本介绍

  问题描述：现有需要装包的物品N件，每件物品的重量为w[i]，每件物品的价值为v[i]，背包的可承重量为W，问背包能够装下的最大价值是多少？如下图，给出了5件物品的重量和价值，现背包容量为20，请问装包的最大价值是多少？装哪些物体？

背包问题参考资料:https://baike.baidu.com/item/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98/2416931?fr=aladdin
讲解视频参考：https://www.bilibili.com/video/BV1U5411s7d7/?spm_id_from=333.337.search-card.all.click&vd_source=1613a057691341621e311fd2c0f53768

1.2 C语言解题

①只输出最大价值的程序：

#include 
#define M 6
#define W 21

int dp[M][W] = {{0}};
int w[M] = {0, 2, 3, 4, 5, 9};
int v[M] = {0, 3, 4, 5, 8, 10};

void fun(int i, int j) {
	if (j < w[i]) dp[i][j] = dp[i-1][j];
	else {
		int tmp1, tmp2;
		tmp1 = dp[i-1][j-w[i]]+v[i];
		tmp2 = dp[i-1][j];
		dp[i][j] = tmp1>tmp2?tmp1:tmp2;
	} 
}

int main() {
	int i, j;
	for (i=1; i<M; i++) {
		for (j=1; j<W; j++) {
			fun(i,j);
		}
	}
	printf("%d", dp[M-1][W-1]);
}

②同时求解最大价值和最优方案
  要求解到底选中了哪些物品，关键在于记录每个dp[i][j]的状态，此处用s[i][j]表示，如果第i件物品被购买了，则令s[i][j]=1，如果不购买，则令s[i][j]=0；当所有状态求解完毕之后，从最后一个状态开始查看，如果s[i][j]=1，表明第i件物品选中了，之后令i=i-1，j=j-w[i]，接着查看s[i-1][j-w[i]]的状态，如果是s[i][j]=0，表明第i件物品不够买，之后i=i-1，但j不变，接着查看s[i-1][j]的状态，以此类推，直到i==0，输出所有选中的物品即可。具体实现方式可参考如下程序：

#include 
#define M 6		// 数量设置比实际多一是为了能够进行[i-1]的索引
#define W 21

int main() {
	int i, j;
	int w[M] = {0, 2, 3, 4, 5, 9};
	int v[M] = {0, 3, 4, 5, 8, 10};
	int dp[M][W] = {{0}}, s[M][W]={{0}};	// s记录物品购买状态
	// 动态规划算法主体
	for (i=1; i<M; i++) {
		for (j=1; j<W; j++) {
			if (j < w[i]) {
				dp[i][j] = dp[i-1][j];
			}
			else {
				int tmp1, tmp2;
				tmp1 = dp[i-1][j-w[i]]+v[i];
				tmp2 = dp[i-1][j];
				if (tmp1>tmp2) {
					dp[i][j] = tmp1;
					s[i][j] = 1;		// 购买物品i时，标记s[i][j]为1
				}
				else dp[i][j]=tmp2;
			} 
		}
	}
	
	// 结果打印
	i = M-1, j = W-1;	// 物品数量和背包容量
	printf("最大装包价值为：%d\n", dp[i][j]);
	printf("需要装包的物品有：");
	do {
		if (s[i][j]==1)	{
			printf("%d ", i);
			j -= w[i];	// i选中后，容量减少；
			i--;		// 接着查看上一件物品是否购买；
		}
		else i--;		// 如果当前物件不选，则直接查看上一物品，j不变；
	}
	while(i!=0);
	printf("\n剩余空间容量：%d", j);
}

1.3 运行结果

①只输出最大价值：

②同时求解最大价值和选中的物品：

  如图所示，在本题中，共有5件物品，在容量为20的情况下，价值最大的选择方式为1，3，4，5物品。
  笔者设想：读者可以罗列自己每天要做的任务N件，并给任务附上耗时w[i]和重要程度v[i]，那么我们在只有T个工作时间的情况下，可以利用本节算法求解出最优的工作选项，这样一来就可以生产效率最大化了，哈哈哈~。

2. dijkstra算法计算单源最短路线问题

2.1 基本介绍

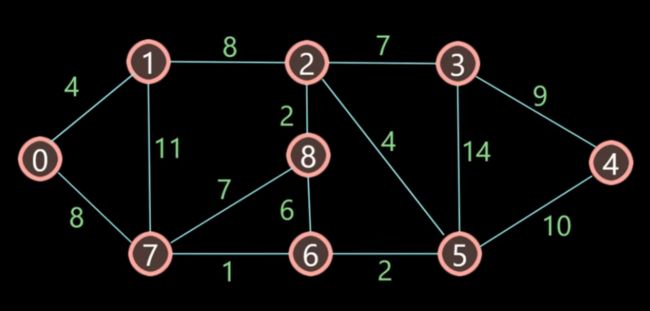
  问题描述：已知N个城市和m条连通城市间的铁路，问从城市A到城市B的最短路径怎么走，最短路径是多少？如下图所示，请问从第0号城市到第4号城市的最短距离是多少，路径怎么走？

dijkstra算法简单易懂介绍视频：
https://www.bilibili.com/video/BV1zz4y1m7Nq/?spm_id_from=333.337.search-card.all.click&vd_source=1613a057691341621e311fd2c0f53768

2.2 C语言解法

#include 
#include 
#define N 9

int main()
{
	int i,j,k,d[N][N]={{0}};
	int e[14][3] = {{0,1,4}, {0,7,8},{1,2,8},\
					{1,7,11},{7,8,7},{7,6,1},\
					{2,3,7}, {2,5,4},{2,8,2},\
					{8,6,6}, {6,5,2},{3,4,9},\
					{3,5,14},{5,4,10}};
	
	// 邻接矩阵初始化流程：除了对角线元素，其余设为无穷大 -> 根据边线信息给矩阵赋值				
	for (i=0;i<9;i++)
	{
		for (j=0;j<9;j++)
		{
			if (i!=j) d[i][j]=1000;
		}
	}
	
	for (i=0;i<14;i++)
	{
		j = e[i][0];
		k = e[i][1];
		d[j][k] = e[i][2];
		d[k][j] = e[i][2];
	}
	
	// 定义始末点、标记集合sign、起点到各点的距离dist、每个最优点的上一节点矩阵front
	int s=0, t=4, tmp=0, min=1000, index=0;
	int sign[N]={0}, dist[N]={0}, front[N]={0};
	
	for (i=0;i<N;i++)	// 起点到其余各点的距离初始化为无穷大
	{
		if (i==s) continue;
		dist[i] = 1000;
	}
	
	// dijkstra算法主体
	sign[s] = 1;
	while(sign[t]!=1)
	{
		min=1000;
		for (i=0;i<N;i++)
		{
			if (sign[i]==1) continue;	// 过滤已标记的节点
			tmp = d[s][i]+dist[s];
			if (dist[i]>tmp)
			{
				dist[i] = tmp;
				front[i] = s;	// 记录最优值的前一个点
			}
			if (min>dist[i])
			{
				min = dist[i];
				index = i;
			}
		}
		s = index;			// 将下一个起点定为最小路径的节点
		sign[s] = 1;		// 将该点作为标记点
	}

	s=0, t=4;
	printf("从节点%d到节点%d的最短距离为：%d", s, t, dist[t]);
	
	printf("\n最短路线为：%d ", t);
	do
	{
		printf("%d ", front[t]); // 输出最短路径路线
		t = front[t];
	}
	while(t!=0);
}

2.3 运行结果

  如下图所示，从0到4的最短距离为21，其路线为0 -> 7 -> 6 -> 5 ->4，注：因为节点是从终点回溯到起点的，所以打印出来的路线为逆序，实际路线是从右往左查看。

3. Floyd算法计算任意两点间的最短路线问题

3.1 基本介绍

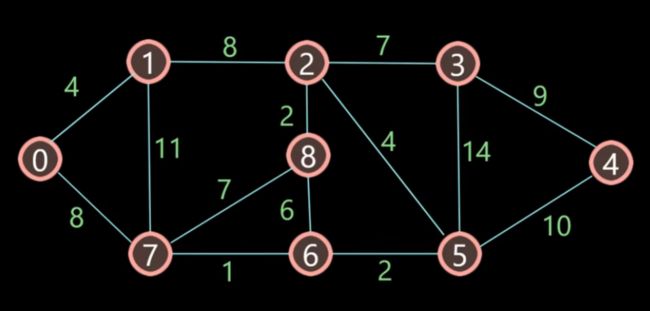
  与上一节同样的问题，不过是利用Floyd算法进行求解。问：任意两点间的最短路线和最短距离是多少？

掌握Floyd算法的资料可参考：https://haokan.baidu.com/v?pd=wisenatural&vid=3162895385654641145
这位老师讲解比较浅显易懂。

3.2 C语言解法

  参考资料中没有介绍如何输出最短路线的方法，本人结合dijkstra算法的思路对floyd算法进行了改进，实现了任意两点间最短路线和最短距离的求解，具体实现方式如下：

#include 
#include 
#define N 9

int main()
{
	int i,j,k,d[N][N]={{0}},front[N][N]={{0}};
	int e[14][3] = {{0,1,4}, {0,7,8},{1,2,8},\
					{1,7,11},{7,8,7},{7,6,1},\
					{2,3,7}, {2,5,4},{2,8,2},\
					{8,6,6}, {6,5,2},{3,4,9},\
					{3,5,14},{5,4,10}};
					
	for (i=0;i<9;i++)
	{
		for (j=0;j<9;j++)
		{
			if (i!=j) d[i][j]=1000;
		}
	}
	
	for (i=0;i<14;i++)
	{
		j = e[i][0];
		k = e[i][1];
		d[j][k] = e[i][2];
		d[k][j] = e[i][2];
	}
	
	// floyd算法：
	for (i=0;i<9;i++)
	{
		for (j=0;j<9;j++)
		{
			front[i][j] = i;	// 用于记录路径
		}
	}
	
	for (k=0;k<N;k++)
	{
		for (i=0;i<N;i++)
		{
			for (j=0;j<N;j++)
			{
				if (d[i][j]>d[i][k]+d[k][j])
				{
					d[i][j] = d[i][k]+d[k][j];
					front[i][j] = front[k][j];	// 每次替换后，变更为上一节点
				}
			}
		}
	}
	
	printf("任意两点间的最短距离：\n");
	for (i=0;i<9;i++)
	{
		for (j=0;j<9;j++)
		{
			printf("%4d ", d[i][j]);
		}
		printf("\n");
	}
	
	int s=1,t=4;
	printf("从%d到%d的最短距离为：%d", s, t, d[s][t]);
	printf("\n路径：%d ", t);
	do
	{
		printf("%d ", front[s][t]);
		t = front[s][t];
	}
	while(t!=s);
}

3.3 运行结果

   如下图，求解从0节点到4节点的最短距离为21，最短路线为：0 -> 7 -> 6 -> 5 -> 4。

   如下图，求解从1节点到4节点的最短距离为22，最短路线为：1 -> 2 -> 5 -> 4。

欢迎各位读者学习交流！