【深度学习】04-01-自注意力机制(Self-attention)-李宏毅老师21&22深度学习课程笔记
04-01-自注意力机制Self-attention
- 模型输入
-
- 文字处理
- 语音处理
- Graph
- 模型输出
-
- 类型一:一对一(Sequence Labeling)
- 类型二:多对一
- 类型三:多对多(由模型自定seq2seq)
- 一对一类型:序列标注问题 - 无上下文信息
- 序列标注问题 - 解决方法一:滑动窗口相邻向量信息
- 序列标注问题 - 解决方法二:Self-attention
- Self-attention
-
- 如何保证每个输出都能分析所有输入上下文? - 关联度
- 如何确定两个输入向量的关联程度α?- 计算关联度的模组(Dot-product & Additive)
-
- 计算关联度的模组 Dot-product(transformer中的方法)
- 计算关联度的模组 Additive
- Self-attention 如何利用 Dot-product 计算出关联度?
-
- 如何基于关联度抽取信息?- 加权求和
- Self-attention 原理
- 多头注意力机制 (Multi-head Self-attention)
-
- 为什么需要多种注意力?- 相关性可能有多种
- 如何计算多头注意力中的相关性?- 按相关类型计算
- 注意力机制问题:没有位置信息
-
- 为什么需要位置信息?- 位置信息很重要
- 如何为Self-attention添加位置信息?- Positional Encoding
-
- 如何表示位置信息 e i e^i ei? - 人工标注 & 数据集训练
-
- 人工标注表示位置信息
- 训练集训练
- 自注意力机制的应用
-
- 语音处理
- 问题:超大输入序列导致复杂度很高 - Truncated Self-attention
- 图像处理
- Self-attention Vs CNN
- Self-attention Vs RNN
- Self-attention 应用图论(GNN)
- Self-attention 众多变形
模型输入
文字处理
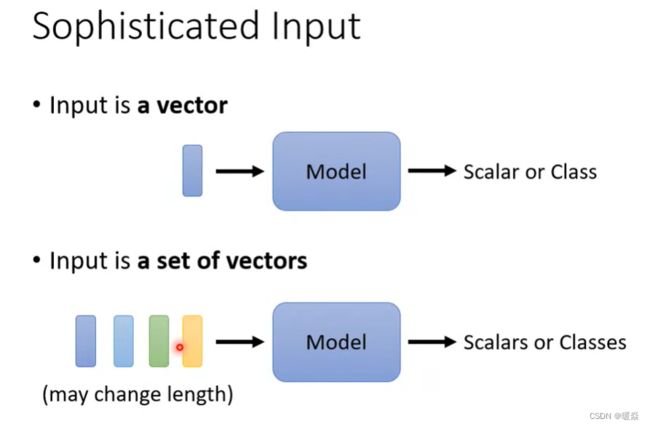
无论是预测视频观看人数还是图像处理,输入都可以看作是一个向量,输出是一个数值或类别。然而,若输入是一系列向量(序列),同时长度会改变,例如把句子里的单词都描述为向量,那么模型的输入就是一个向量集合,并且每个向量集合的大小都不一样。
一种将单词表示为向量的方法:One-hot Encoding(独热编码)。
向量的长度就是世界上所有词汇的数目,用不同位的1(其余位置为0)表示一个词汇,如下所示:
apple = [1, 0, 0, 0, 0, …]
bag = [0, 1, 0, 0, 0, …]
cat = [0, 0, 1, 0, 0, …]
dog = [0, 0, 0, 1, 0, …]
computer = [0, 0, 0, 0, 1, …]
但是这种表示方式默认了所有词汇间没有任何关系,猫和狗都是动物这种关系在向量集中体现不出来,里面没有任何有意义的信息。
one hot representation编码的每个单词都是一个维度,彼此independent。
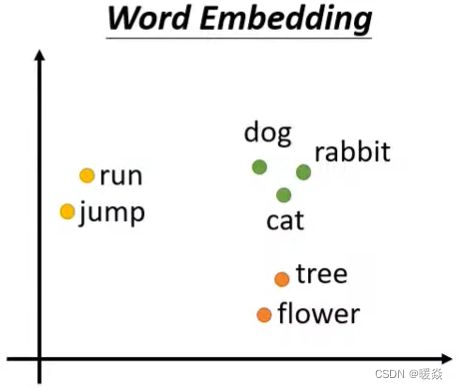
另一种将单词表示为向量方法:Word Embedding。
给单词一个向量,这个向量有语义的信息,一个句子就是一排长度不一的向量。将Word Embedding画出来,就会发现同类的单词就会聚集,因此它能区分出类别:
To learn more: https://youtu.be/X7PH3NuYW0Q (in Mandarin)
什么是 word embedding? - YJango的回答 - 知乎
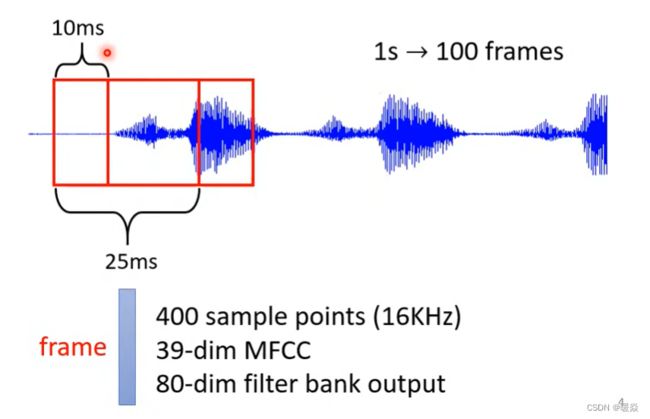
语音处理
取一段语音信号作为窗口,可以将10ms内的信息描述为一个向量(帧),滑动这个窗口就得到这段语音的所有向量(一个向量集)。
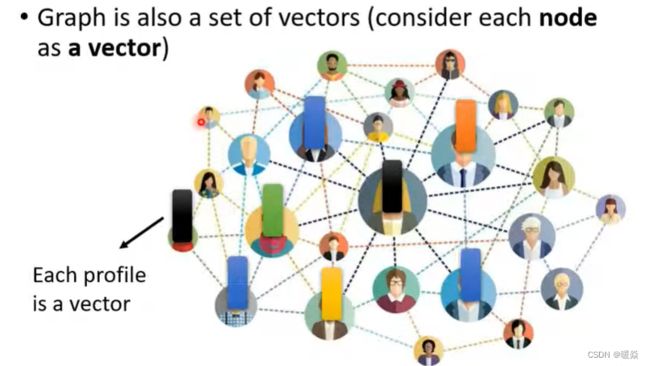
Graph
社交网络的每个节点就是一个人,节点之间的关系用线连接。每一个人就是一个向量。
分子上的每个原子就是一个向量(每个元素可用One-hot编码表示),分子就是一堆向量。
模型输出
按照输入向量与输出标签的数量关系,可以分为一对一、多对一及多对多。
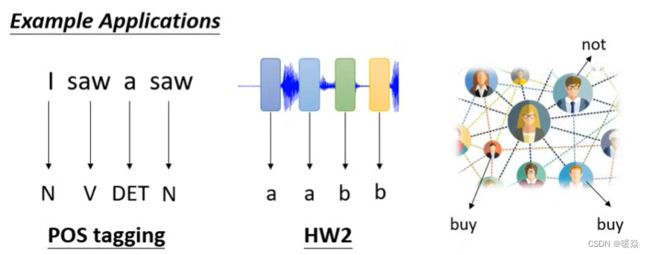
类型一:一对一(Sequence Labeling)
文字处理:词性标注(每个输入的单词都输出对应的词性)。
语音处理:一段声音信号里面有一串向量,每个向量对应一个音标。
图像处理:在社交网络中,推荐某个用户商品(可能会买或者不买)。
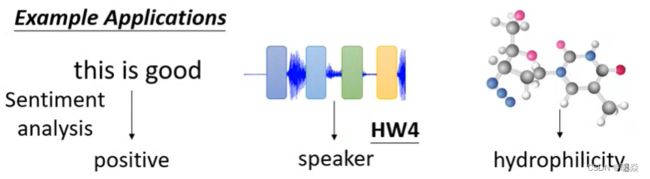
类型二:多对一
多个输入向量对应一个输出标签。
语义分析:正面评价、负面评价。
语音识别:识别某人的音色。
图像:给出分子的结构,判断其亲水性。
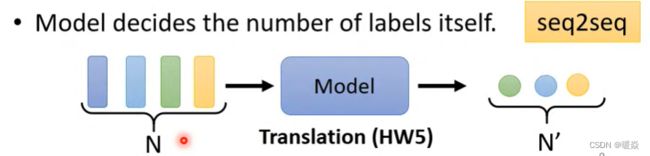
类型三:多对多(由模型自定seq2seq)
翻译:语言A到语言B,单词字符数目不同
语音识别
接下来先讨论一对一类型。
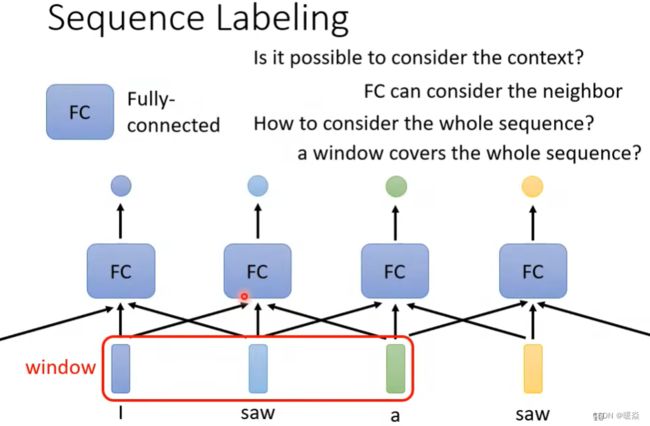
一对一类型:序列标注问题 - 无上下文信息
序列标注:Sequnce Labeling
利用全连接网络,输入一个句子,输出对应单词数目的标签。
问题:当一个句子里出现两个相同的单词,并且它们的词性不同(例如:I saw a saw. 我看见一把锯子)。期望模型输出第一个saw为动词,第二个saw为名词,但是这种结构的神经网络不可能做到。
序列标注问题 - 解决方法一:滑动窗口相邻向量信息
解决:让神经网络考虑上下文,利用滑动窗口,每个向量查看窗口中相邻的其他向量的性质。
考虑整条语句分析的情况,需要获取整条语句的词汇信息,需要滑动窗口包含语句所有词汇的向量,这样会导致全连接神经网络的参数暴增,进而导致超大运算量甚至是过拟合。
所以,这种方法不能解决整条语句的分析问题,即语义分析。这就引出了 Self-attention 技术。
序列标注问题 - 解决方法二:Self-attention
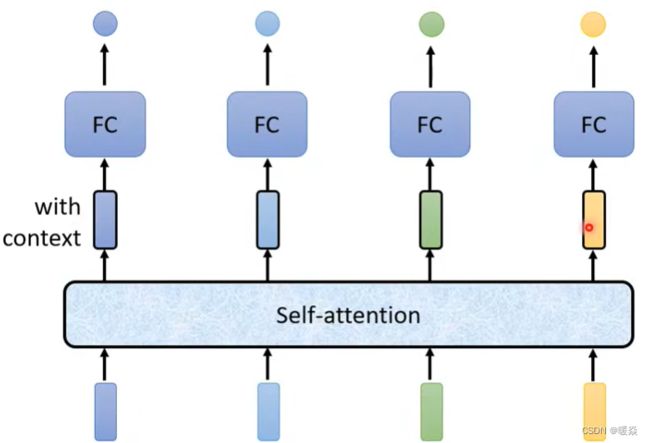
输入整个语句的向量到self-attention中,输出相等个数的向量,且输出的每个向量都考虑输入的整个语句向量集的信息。
一种方式是考虑训练集中最长的语句的长度作为滑动窗口的尺寸,这意为着Fully Connected Network需要大量参数,运算量很大,而且容易overfeating。
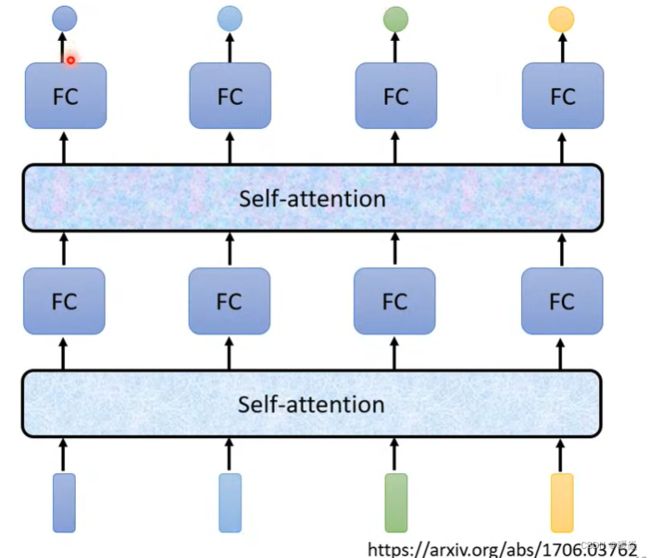
输入整个语句的向量到self-attention中,输出对应个数的向量,再将其结果输入到全连接网络,最后输出标签。以上过程可多次重复,fully connected network 与 self-attention 交替使用:
Google 根据自注意力机制在论文 Attention is all you need 中提出了 Transformer 架构,注意力机制在该论文之前就已经存在,但是,是在Attention is all you need论文中将注意力机制称为Self-attention,并使其发扬光大。
self attention :专注整个序列的信息。FC:专注某个位置的信息
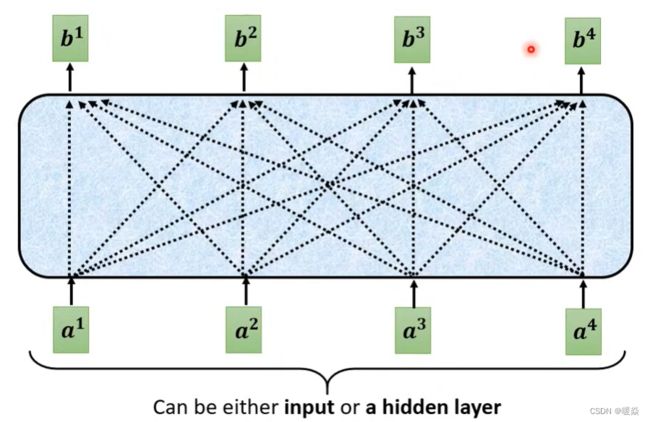
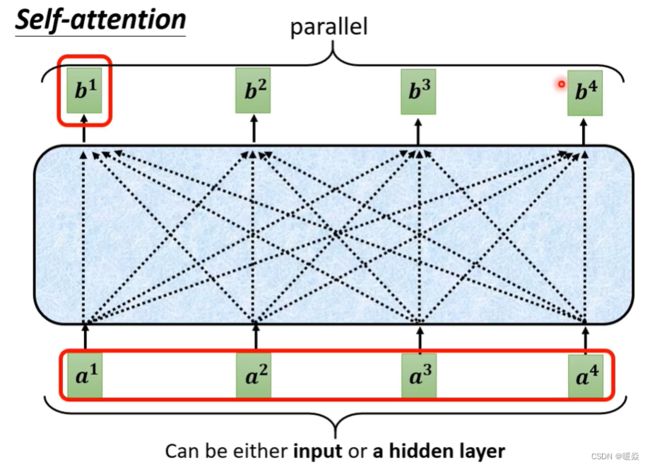
Self-attention
a表示输入层或隐藏层,每个输出b与所有输入a都相关。
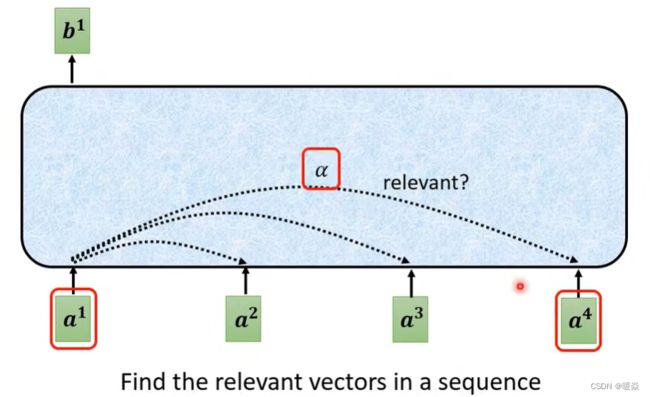
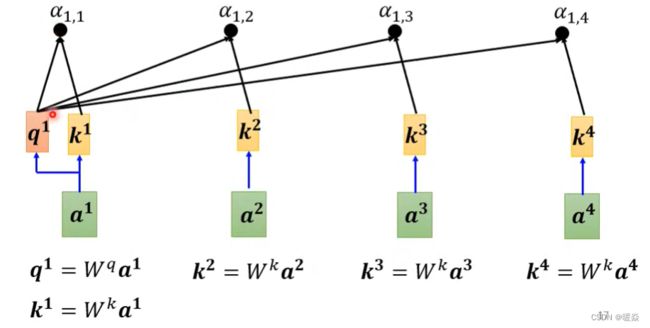
如何保证每个输出都能分析所有输入上下文? - 关联度
α 表示a1与a4的关联程度。又称为 attention score。
在类似语义分析的任务场景中,每个输出b都需要分析所有a,但是使用滑动窗口又会导致参数量暴增,所以需要根据a1找出输入向量集中 哪些向量与 ’ 判断a1的类别 ’ 相关。
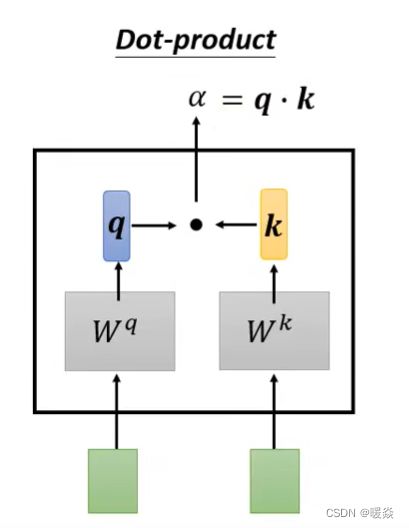
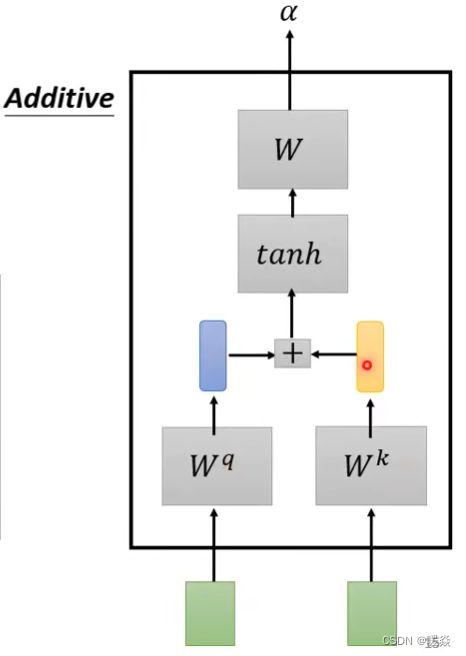
如何确定两个输入向量的关联程度α?- 计算关联度的模组(Dot-product & Additive)
计算关联度的模组很多,输入两个[输入向量],输出两个[输入向量]的关联程度。
下面的讲解以 Dot-product 和 Additive 为例。
计算关联度的模组 Dot-product(transformer中的方法)
计算关联度的模组 Additive
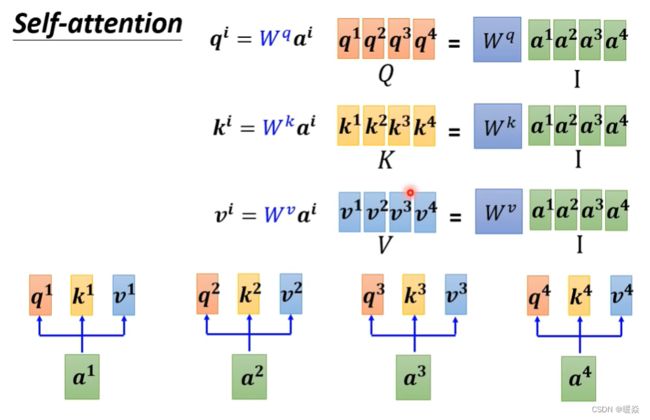
Self-attention 如何利用 Dot-product 计算出关联度?
注意:a1与自己也要计算关联程度。
【待补充】a1与自己计算关联程度的重要性?
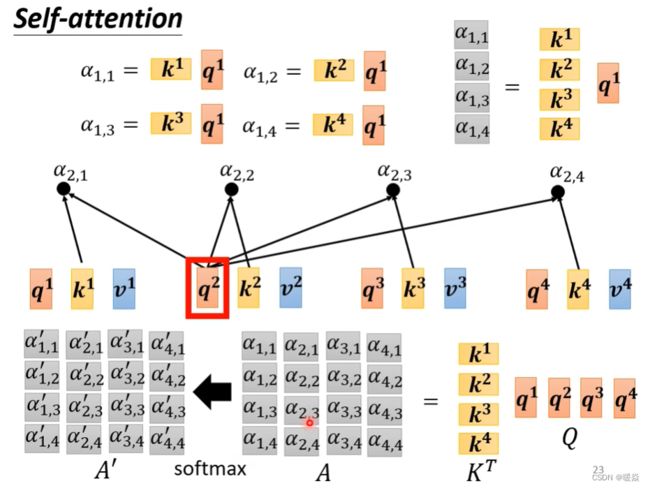
α i , j 表示两个输入向量的关联程度 < / f o n t > , \alpha_{i,j}表示两个输入向量的关联程度, αi,j表示两个输入向量的关联程度</font>,通过 q i q^i qi和 k j k^j kj的内积运算得到,其中i表示 q i q^i qi是由 a i a_i ai计算出来的,j表示 k j k^j kj是由 a j a_j aj计算出来的
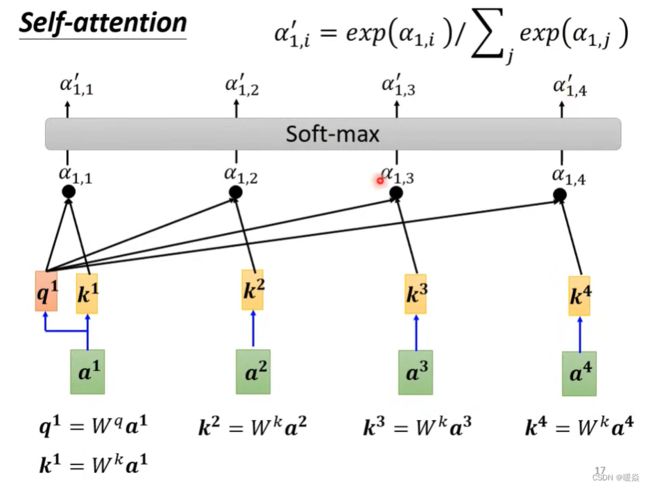
计算出相关性之后,可加一层softmax层(也可以加别的激活函数,比如ReLu)。
注: b i ( 1 ≤ i ≤ 4 ) b^i (1≤i≤4) bi(1≤i≤4) 是同时计算出来的。
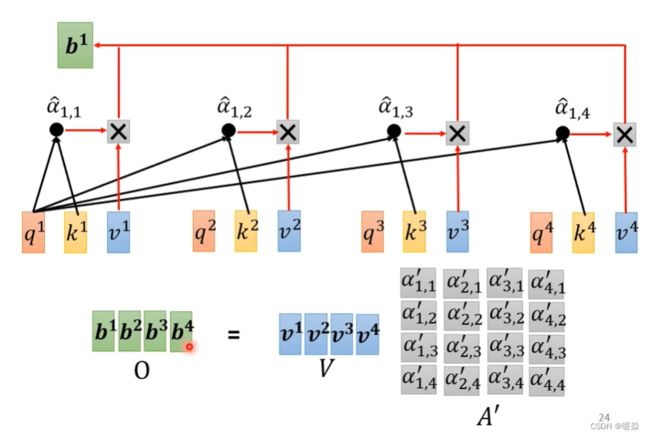
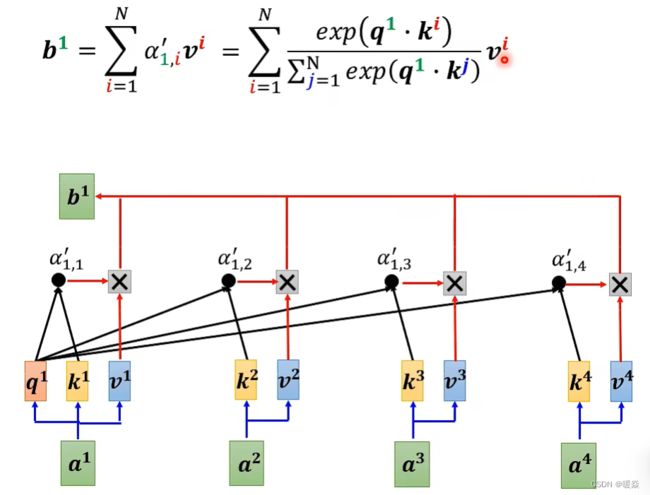
如何基于关联度抽取信息?- 加权求和
哪个 a i j ′ × v i a'_{ij} × v^i aij′×vi 更大,哪个 a 1 a^1 a1就更能决定结果 b i b_i bi
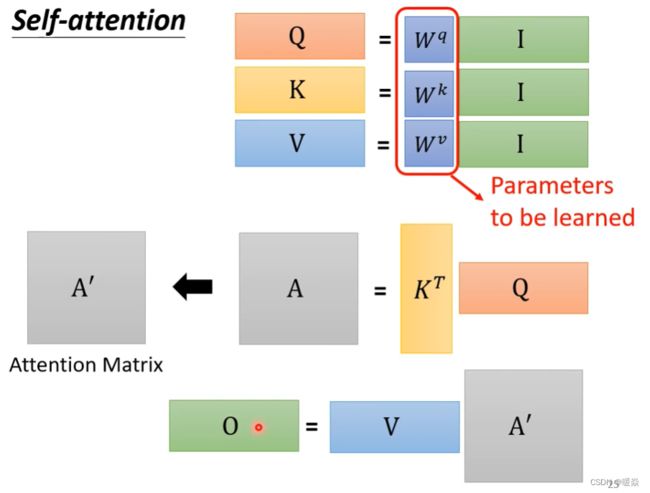
Self-attention 原理
这里需要三个向量:Query,Key,Value。其解释参考文章 《如何理解 Transformer 中的 Query、Key 与 Value》- yafee123
注意:KTQ的结果A,需要经过SoftMax处理。
上述过程可以总结为:
① 输入矩阵 I I I分别乘以 W q , W k , W v W^q,W^k,W^v Wq,Wk,Wv得到三个矩阵 Q , K , V Q,K,V Q,K,V。
② A = K T Q A=K^TQ A=KTQ,经过激活函数处理得到注意力矩阵 A ′ = s o f t m a x ( K T Q d k ) A'=softmax(\frac {K^TQ}{\sqrt{d_k}}) A′=softmax(dkKTQ)
③ 输出 O = V A ′ O=VA' O=VA′
即:
A t t e n t i o n ( Q , K , V ) = V ⋅ s o f t m a x ( K T Q d k ) Attention(Q,K,V) = V \cdot softmax(\frac {K^TQ}{\sqrt{d_k}}) Attention(Q,K,V)=V⋅softmax(dkKTQ)
其中, d k \sqrt{d_k} dk为向量长度。唯一要训练出的参数就是 W q , W k , W v W^q,W^k,W^v Wq,Wk,Wv。
注意力系数计算:
阶段1:根据Query和Key计算两者的相似性或者相关性
阶段2:对第一阶段的原始分值进 行归一化处理
阶段3:根据权重系数对Value进行加权求和,得到Attention Value
所有输入向量中,谁的 attention score 大,谁就能决定Attention Value,即b。
具体计算参考:动手推导Self-Attention
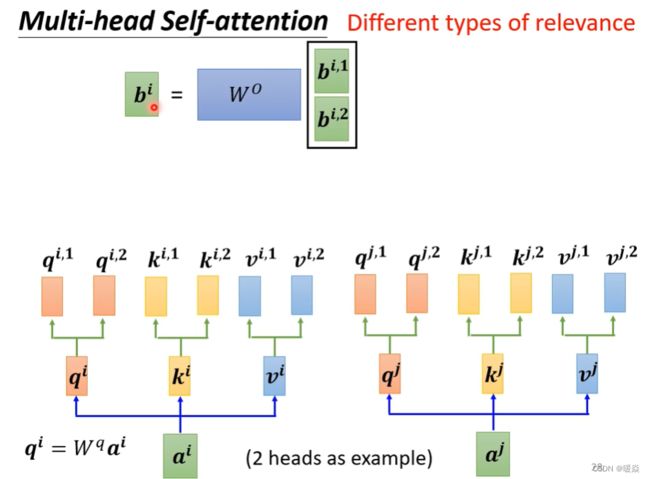
多头注意力机制 (Multi-head Self-attention)
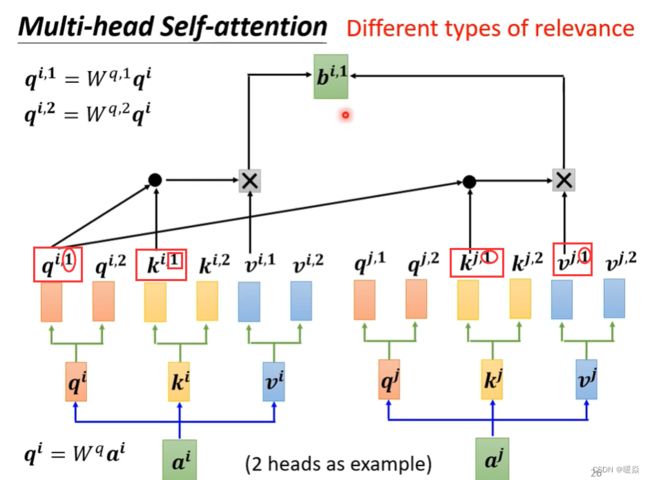
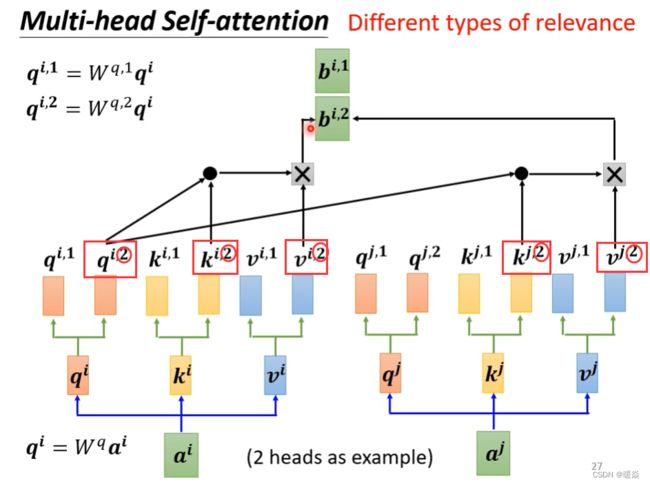
为什么需要多种注意力?- 相关性可能有多种
有些任务(例如:翻译、语音辨识等)中,multi-head会得到更好的结果。
之前的例子,都是用Q去找K,来计算相关性。但是两个事物之间相关性可能有多种不同的类型。因此设置多种Q(head),多种K(Key),多种V(Value),不同的Q来负责不同的相关性。
head的个数是超参数。
如何计算多头注意力中的相关性?- 按相关类型计算
所有 b i , j b^{i,j} bi,j单独计算,同时得出。比如 b i , 1 b^{i,1} bi,1, b i , 2 b^{i,2} bi,2, b i , 3 b^{i,3} bi,3单独计算同时得出。
如上述公式,在Multi-head的情况下,输入还是Q,K,V,输出是不同head的输出的拼接结果,再投影到 W 0 W^0 W0中。其中,对每一个head,可以将 Q,K,V 通过不同的可学习的参数 W Q , W K , W V W^Q,W^K,W^V WQ,WK,WV 投影到一个低维上面,再做注意力函数Attention,最后输出结果。
Query,Key,Value首先经过一个线性变换,然后输入到放缩点积attention,注意这里要做 h 次,其实也就是所谓的多头,每一次算一个头。而且每次Q,K,V进行线性变换的参数W是不一样的 W Q , W K , W V W^Q,W^K,W^V WQ,WK,WV 。然后将 h 次的放缩点积attention结果进行拼接,再进行一次线性变换得到的值作为多头attention的结果。
注意力机制问题:没有位置信息
在语义分析任务中,对于Self-attention来说,并没有序列中字符位置的信息。之前的计算过程中,字母右上角出现的数字,与位置信息无关,只是为了讲解而标注的。
为什么需要位置信息?- 位置信息很重要
在语义分析任务中,例如动词是不太可能出现在句首的,因此可以降低动词在句首的可能性,但是自注意力机制并没有该能力。因此需要加入 Positional Encoding 的技术来标注每个词汇在句子中的位置信息。
如何为Self-attention添加位置信息?- Positional Encoding
每一个不同的位置都有一个专属的向量 e i e^i ei,然后再做 e i + a i e^i+a^i ei+ai 的操作,之后的计算看到 e i e^i ei 就知道 a i a^i ai 的位置是 i i i。
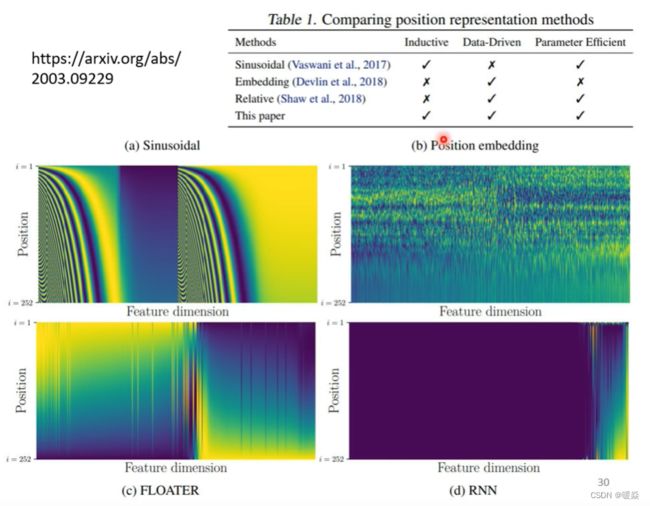
如何表示位置信息 e i e^i ei? - 人工标注 & 数据集训练
人工标注表示位置信息
如下图所示,在attention is all you need论文中, e i e^i ei为图中的一列。
这种 e i e^i ei 是人工标注(hand-crafted)的。就会出现很多问题:在确定 e i e^i ei 的时候只定到128,但是序列长度是129。在最早的论文attention is all you need中是没有这个问题的,它通过某个规则(sin、cos函数)产生。
位置编码如何表示更好?是一个待研究的问题。
训练集训练
位置编码可以自定义表示方法,也可以通过对训练集学习来得出。
下图展示的是几种位置表示方法的效果。
自注意力机制的应用
Transformer 、BERT 模型用到了自注意力机制。
![]()
Self-attention 还可以用在除NLP以外的问题上:语音处理,图像处理。
语音处理
问题:超大输入序列导致复杂度很高 - Truncated Self-attention
attention matrix复杂度是输入向量个数的平方,在语音处理任务中,假设一个向量表示10ms内的语音信息,那么一段语音将由上千个向量组成,这将导致语音处理任务的计算量很大,并且需要很大的存储空间记录计算信息。

针对该问题,提出了 Truncated Self-attention 思想。计算注意力时,只关注小范围(自定义)上下文信息,而不是整句的上下文信息,加快运算速度,节省存储空间。
考虑多大范围内的上下文信息,视任务而定。
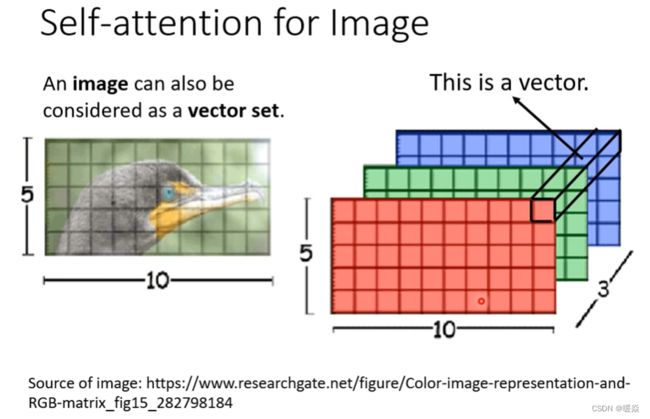
图像处理
使用CNN时,一张图片可看做一个很长的向量。
一张图片也可看做一组向量:一张5∗10的RGB图像可以看做5∗10的三个(通道)矩阵,把一个像素的三个通道数值看作一个三维向量。
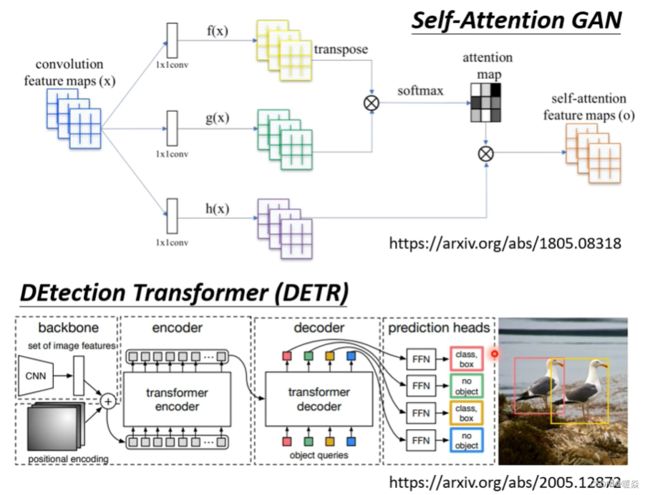
既然一张图片可以看做一组向量,那么也可以使用self-attention进行图像处理。例如:GAN、DETR。
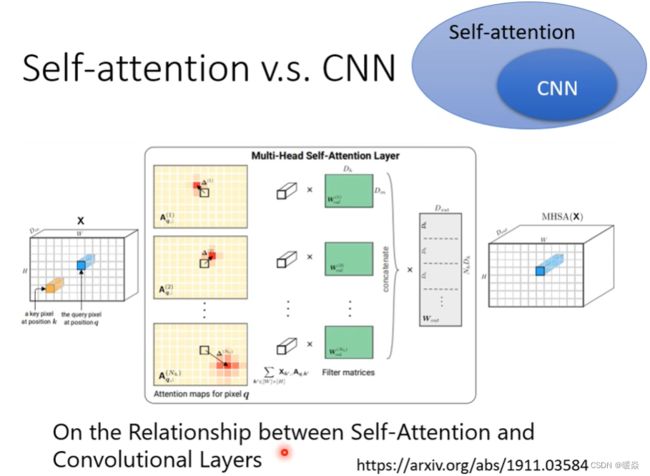
Self-attention Vs CNN
CNN只考虑感受野中的信息。Self-attention考虑整张图片的信息。
CNN是简化版的Self-attention。Self-attention是复杂化的CNN。CNN中感受野的大小是自定义的,Self-attention中使用attention找出相关的像素,这些相关的像素可以看作是自动学习得到的“感受野”。
在论文On the Relationship between Self-Attention and Convolutional Layers中,用数学严谨的证明了CNN就是self-attention的特例,self-attention只要设置合适的参数可以做到CNN同样的效果。
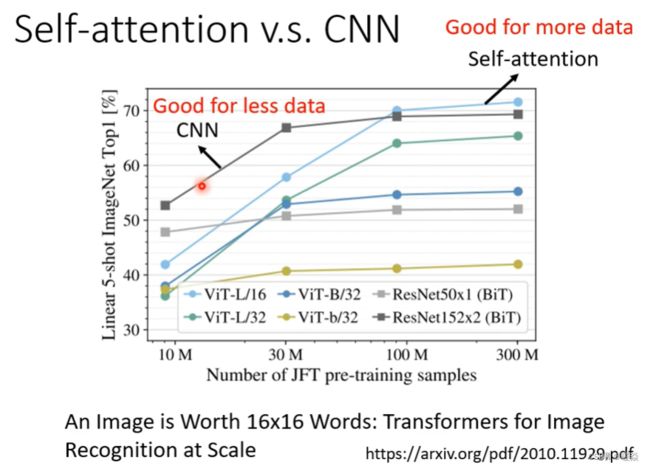
如果用不同的数据量来训练CNN和self-attention,会出现不同的结果。大模型self-attention弹性大,需要更多的训练数据,如果用少量数据训练,容易出现过拟合;而小的模型CNN弹性小,在少量数据集上不容易出现过拟合,但在大数据集
相关论文:An Image is Worth 16×16 Words: Transformers for Image Recognition at Scale
Self-attention Vs RNN
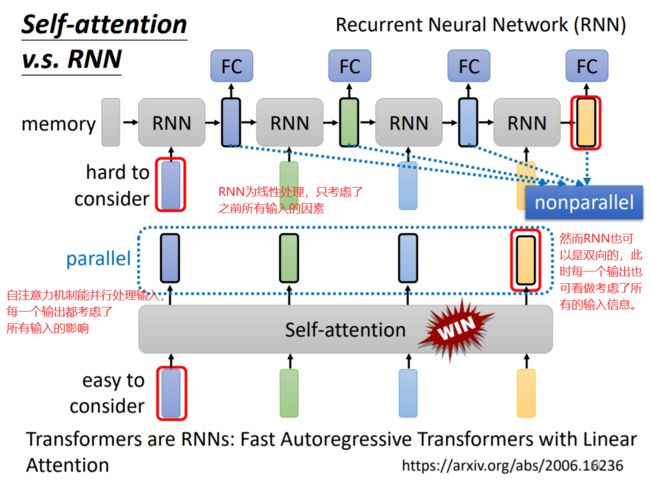
1 RNN中,如果想让后面的RNN考虑前面RNN的输入,就需要memory保存前面RNN的输入。而self-attention中每一个输出都分析了所有输入的信息。
2 RNN中,不能平行处理数据,每一层RNN只考虑前一层的输出。而self-attention中可以平行处理数据,同时计算注意力并得到输出。
3 可以使用双向RNN实现跟self-attention一样考虑所有input sequence的功能。但是,即使使用双向RNN,上图中最右FC(黄)想考虑最左输入(蓝),需要memory保存最左输入,一直保存传递到最右FC。
因此很多的应用逐渐把RNN的架构改为Self-attention架构。
在论文Transformers are RNNs: Fast autoregressive transformers with linear attention中,详细介绍了Self-attention 与 RNN的关系,self-attention加上其他结构可等效于RNN。
Self-attention 应用图论(GNN)
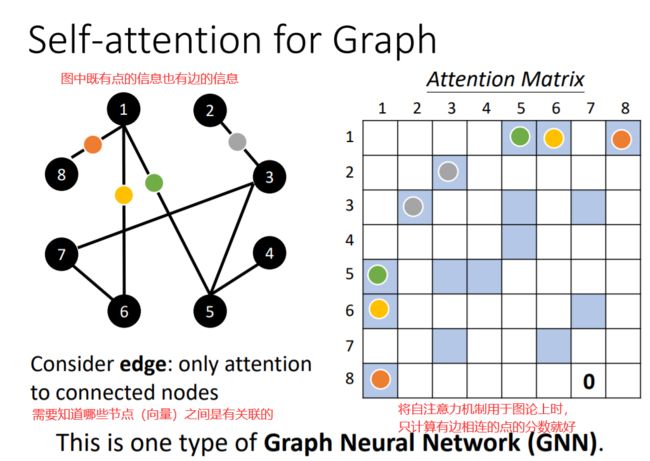
GNN:Graph Neural Network
将图中使用Self-attention,图中顶点的关联关系不需要经过学习得到,关联关系可以直接根据边得到。
Self-attention 众多变形
自注意力机制的缺点就是计算量非常大,因此如何优化其计算量是未来研究的重点,所以出现了很多Self-attention的变形。
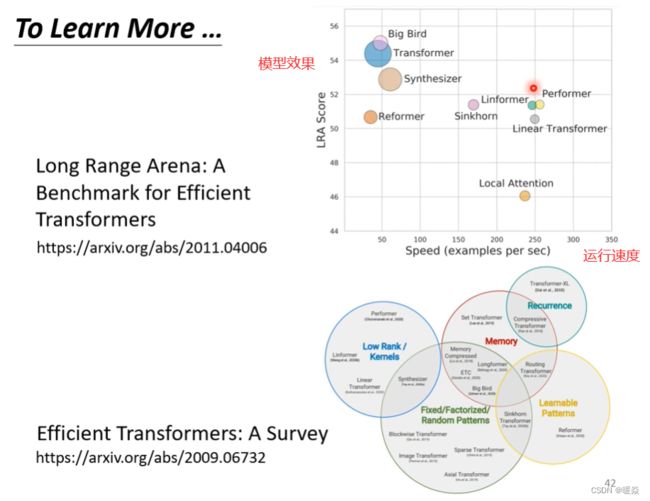
以下论文中,分析了多种self-attention的变形。
Long Range Arena: A Benchmark for Efficient Transformers
Efficient Transformers: A Survey