二维泊松方程求解--点迭代法
本文目录
- 1. 问题描述
-
- 1.1. 泊松方程
- 1.2. 算例
- 2. 区域离散和方程离散
-
- 2.1. 边界条件
- 3. 代数方程组求解
-
- 3.1. 雅可比迭代
- 3.2. 高斯-赛德尔迭代
- 3.3. SOR迭代
- 3.4. 迭代收敛标准
- 3.5. 迭代法收敛的分析
- 3.6. 上述迭代方法的计算结果
- 4. 代码
1. 问题描述
本算例来自B站Up主“Red-Green鲤鱼”的系列教程。本文主要介绍计算代数方程组的三种点迭代方法。
1.1. 泊松方程
含有二阶偏导数的偏微分方程：
∂ 2 ϕ ∂ x 2 + ∂ 2 ϕ ∂ y 2 = f ( x , y ) \frac{\partial^2 \phi}{\partial x^2}+\frac{\partial^2 \phi}{\partial y^2}=f(x,y) ∂x2∂2ϕ+∂y2∂2ϕ=f(x,y)
当 f = 0 f=0 f=0时，上述方程被称为拉普拉斯方程。许多物理过程都可以用泊松方程来描述，如热传导方程
∂ ϕ ∂ t = ∂ 2 ϕ ∂ x 2 + ∂ 2 ϕ ∂ y 2 \frac{\partial \phi}{\partial t}=\frac{\partial^2 \phi}{\partial x^2}+\frac{\partial^2 \phi}{\partial y^2} ∂t∂ϕ=∂x2∂2ϕ+∂y2∂2ϕ
在求解不可压缩流动的NS方程时，通常将已知压力场代入动量方程来预估速度场，然后将预估的速度场代入连续性方程中，由于预估的速度场中包含压力梯度项，因此代入连续性方程后会得到 ∇ ⋅ ( ∇ P ) \nabla \cdot(\nabla P) ∇⋅(∇P)，即压力泊松方程
1.2. 算例
令上述泊松方程的源项为如下形式：
f ( x , y ) = − 4 ⋅ s i n ( x − y ) ⋅ e ( x − y ) f(x,y)=-4\cdot sin(x-y)\cdot e^{(x-y)} f(x,y)=−4⋅sin(x−y)⋅e(x−y)
其解析解为
ϕ ( x , y ) = c o s ( x − y ) ⋅ e ( x − y ) \phi(x,y)=cos(x-y)\cdot e^{(x-y)} ϕ(x,y)=cos(x−y)⋅e(x−y)
比较数值解与解析解在定义域 x ∈ [ − 1 , 1 ] , y ∈ [ − 1 , 1 ] x\in [-1,1], y\in [-1,1] x∈[−1,1],y∈[−1,1]上的差别。边界条件为Dirichlet，边界上的值由解析解求出。
2. 区域离散和方程离散
x x x方向设置 N N N个结点，编号从 1 − N 1-N 1−N， y y y方向上设置 M M M个结点，编号从 1 − M 1-M 1−M，结点间距分别为 Δ x \Delta x Δx和 Δ y \Delta y Δy，将 ( i , j ) (i,j) (i,j)号结点记为 P P P，该结点上下左右四个结点分别记为 N , S , W , E N,S,W,E N,S,W,E
采用有限差分法计算泊松方程，二阶偏导数项采用二阶中心差分离散，
∂ 2 ϕ ∂ x 2 ∣ P = ϕ W + ϕ E − 2 ϕ P Δ x 2 \frac{\partial^2 \phi}{\partial x^2}\bigg|_P=\frac{\phi_W+\phi_E-2\phi_P}{\Delta x^2} ∂x2∂2ϕ∣∣∣∣P=Δx2ϕW+ϕE−2ϕP
∂ 2 ϕ ∂ y 2 ∣ P = ϕ N + ϕ S − 2 ϕ P Δ y 2 \frac{\partial^2 \phi}{\partial y^2}\bigg|_P=\frac{\phi_N+\phi_S-2\phi_P}{\Delta y^2} ∂y2∂2ϕ∣∣∣∣P=Δy2ϕN+ϕS−2ϕP
ϕ W + ϕ E − 2 ϕ P Δ x 2 + ϕ N + ϕ S − 2 ϕ P Δ y 2 = f P \frac{\phi_W+\phi_E-2\phi_P}{\Delta x^2}+\frac{\phi_N+\phi_S-2\phi_P}{\Delta y^2}=f_P Δx2ϕW+ϕE−2ϕP+Δy2ϕN+ϕS−2ϕP=fP
ϕ P = ( ϕ W + ϕ E ) Δ y 2 + ( ϕ N + ϕ S ) Δ x 2 − f P Δ x 2 Δ y 2 2 ( Δ x 2 + Δ y 2 ) \phi_P=\frac{(\phi_W+\phi_E)\Delta y^2+(\phi_N+\phi_S)\Delta x^2-f_P \Delta x^2 \Delta y^2}{2(\Delta x^2+\Delta y^2)} ϕP=2(Δx2+Δy2)(ϕW+ϕE)Δy2+(ϕN+ϕS)Δx2−fPΔx2Δy2
令 Δ x = Δ y = h \Delta x=\Delta y=h Δx=Δy=h，则上式化为
ϕ P = 1 4 ( ϕ W + ϕ E + ϕ N + ϕ S − h 2 f P ) \phi_P=\frac{1}{4}(\phi_W+\phi_E+\phi_N+\phi_S-h^2f_P) ϕP=41(ϕW+ϕE+ϕN+ϕS−h2fP)
2.1. 边界条件
左边界
ϕ 1 , j = c o s ( − 1 − y j ) ⋅ e ( − 1 − y j ) \phi_{1,j}=cos(-1-y_j)\cdot e^{(-1-y_j)} ϕ1,j=cos(−1−yj)⋅e(−1−yj)
右边界
ϕ N , j = c o s ( 1 − y j ) ⋅ e ( 1 − y j ) \phi_{N,j}=cos(1-y_j)\cdot e^{(1-y_j)} ϕN,j=cos(1−yj)⋅e(1−yj)
下边界
ϕ i , 1 = c o s ( x i + 1 ) ⋅ e ( x i + 1 ) \phi_{i,1}=cos(x_i+1)\cdot e^{(x_i+1)} ϕi,1=cos(xi+1)⋅e(xi+1)
上边界
ϕ i , N = c o s ( x i − 1 ) ⋅ e ( x i − 1 ) \phi_{i,N}=cos(x_i-1)\cdot e^{(x_i-1)} ϕi,N=cos(xi−1)⋅e(xi−1)
3. 代数方程组求解
上一篇文章介绍了代数方程组求解方法中的直接解法TDMA，本文介绍另一大类求解方法：迭代法。迭代法的思想也可以概况为“预测-校正”，给出初始值，通过不断迭代逐步改进，直到达到一定精度要求为止。
该方法需要首先构造迭代方式；其次是所构造的迭代序列是否收敛，如果收敛则要进一步提高收敛速度。
迭代法可分为点迭代、块迭代、交替方向迭代法以及强隐迭代法。在点迭代法中，每一步计算只能改进求解区域中一个结点的值，且该值是由一个显函数形式由其余各点的已知值来确定，因而点迭代法又称为显式迭代法。
下面将讨论点迭代法的三种实施方式。
3.1. 雅可比迭代
ϕ P n + 1 = 1 4 ( ϕ W n + ϕ E n + ϕ N n + ϕ S n − h 2 f P ) \phi_P^{n+1}=\frac{1}{4}(\phi_W^n+\phi_E^n+\phi_N^n+\phi_S^n-h^2f_P) ϕPn+1=41(ϕWn+ϕEn+ϕNn+ϕSn−h2fP)
上式中上标 n n n为当前预测值， n + 1 n+1 n+1为代入迭代方程后的校正值
3.2. 高斯-赛德尔迭代
ϕ P n + 1 = 1 4 ( ϕ W n + 1 + ϕ E n + ϕ N n + ϕ S n + 1 − h 2 f P ) \phi_P^{n+1}=\frac{1}{4}(\phi_W^{n+1}+\phi_E^n+\phi_N^n+\phi_S^{n+1}-h^2f_P) ϕPn+1=41(ϕWn+1+ϕEn+ϕNn+ϕSn+1−h2fP)
在逐点计算过程中， W W W和 S S S点的值在本次迭代过程中已知，因此将已知值代入迭代方程中
3.3. SOR迭代
Successive Over Relaxation，逐次超松弛。SOR迭代法收敛的充要条件是松弛因子 0 < β < 2 0<\beta <2 0<β<2，当 β > 1 \beta>1 β>1时能够起到加速收敛的效果。
ϕ P n + 1 = β 4 ( ϕ W n + 1 + ϕ E n + ϕ N n + ϕ S n + 1 − h 2 f P ) + ( 1 − β ) ϕ P n \phi_P^{n+1}=\frac{\beta}{4}(\phi_W^{n+1}+\phi_E^n+\phi_N^n+\phi_S^{n+1}-h^2f_P)+(1-\beta)\phi_P^n ϕPn+1=4β(ϕWn+1+ϕEn+ϕNn+ϕSn+1−h2fP)+(1−β)ϕPn
当 β = 1 \beta=1 β=1，SOR迭代退化为Gauss-Seidel. 在《Computational Methods for Fluid Dynamics》第四版5.3.3节给出了一些关于SOR的讨论。
上述方程变换形式可得
ϕ n + 1 = ϕ n + β ( ϕ G S n + 1 − ϕ n ) \phi^{n+1}=\phi^n+\beta(\phi_{GS}^{n+1}-\phi^n) ϕn+1=ϕn+β(ϕGSn+1−ϕn)
其中 ϕ G S \phi_{GS} ϕGS为Gauss-Seidel法求出的值。进一步移项， β \beta β用其他几项表示，可以得出 β > 1 \beta>1 β>1能够加速迭代，即缩小初始值变化到最终值所需时间。
3.4. 迭代收敛标准
本文使用如下标准来定义收敛标准
R e s i d u a l = 1 N ∑ i = 1 N ∣ ϕ i n + 1 − ϕ i n ∣ ∣ ϕ i n + 1 + ε ∣ < 1 0 − 5 Residual=\frac{1}{N}\sum_{i=1}^{N}\frac{|\phi_i^{n+1}-\phi_i^{n}|}{|\phi_i^{n+1}+\varepsilon|}<10^{-5} Residual=N1i=1∑N∣ϕin+1+ε∣∣ϕin+1−ϕin∣<10−5
此处 N N N为全局结点个数，上式表示结点平均相对偏差小于 1 0 − 5 10^{-5} 10−5时，认为达到收敛。 ε \varepsilon ε为极小值，防止分母为0
除此之外，《数值传热学》还介绍了其他收敛标准。
3.5. 迭代法收敛的分析
《数值传热学》第二版7.4节写道，对于如下形式的方程：
a P T P = ∑ a n b T n b + b a_PT_P=\sum a_{nb}T_{nb} +b aPTP=∑anbTnb+b
Jacobi与Gauss-Seidel迭代法收敛的一个充分条件是：系数矩阵不可约且按行或按列弱对角占优。其中“弱对角占优”需满足：
∑ ∣ a n b ∣ ∣ a P ∣ ≤ 1 o r ∣ a P ∣ ≥ ∑ ∣ a n b ∣ \frac{\sum |a_{nb}|}{|a_P|}\leq 1 \quad or \quad |a_P| \ge \sum |a_{nb}| ∣aP∣∑∣anb∣≤1or∣aP∣≥∑∣anb∣
对各行成立，且其中至少对一行不等号成立。在本文的算例中，系数矩阵的第一行和最后一行对应为不等号，其他各行均是等号成立，即 ∣ a P ∣ = ∑ ∣ a n b ∣ |a_P| = \sum |a_{nb}| ∣aP∣=∑∣anb∣
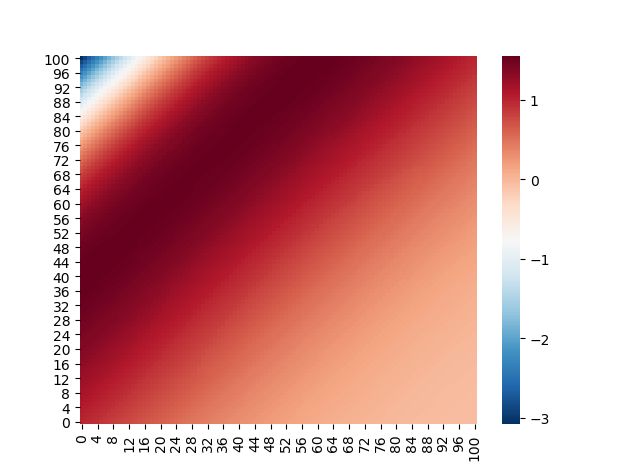
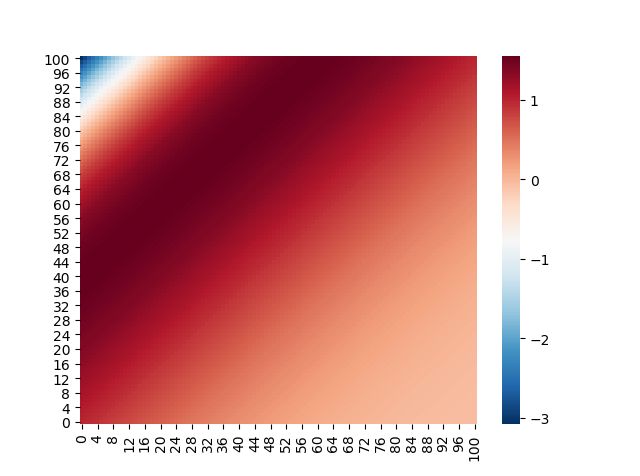
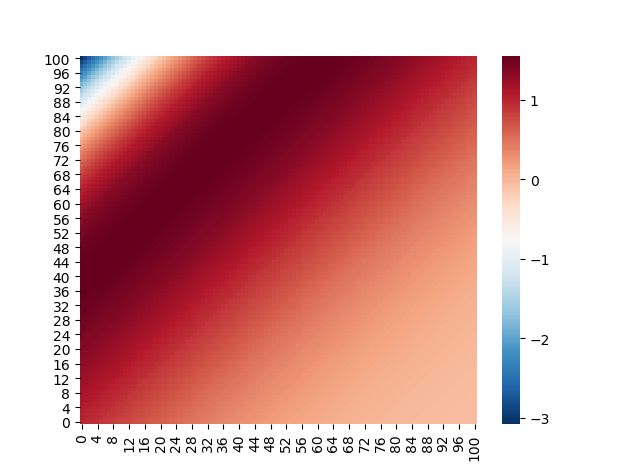
3.6. 上述迭代方法的计算结果
两个方向各自的结点数 N = 101 N=101 N=101
| Method | Iteration number |
|---|---|
| Jacobi | 9141 |
| GS | 5121 |
| SOR, β = 1.5 \beta=1.5 β=1.5 | 2065 |
| SOR, β = 1.9 \beta=1.9 β=1.9 | 403 |
Jacobi
Gauss-Seidel
SOR, β = 1.5 \beta=1.5 β=1.5
SOR, β = 1.9 \beta=1.9 β=1.9
Analytical solution
4. 代码
代码链接