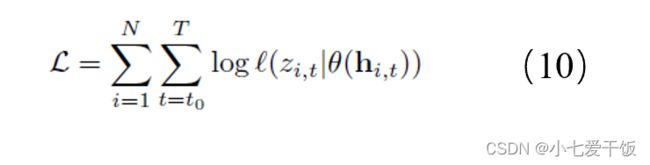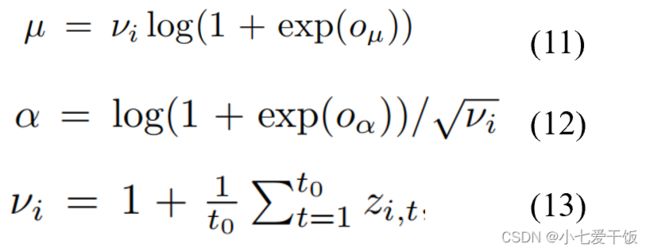时间序列预测之DeepAR

目录

前言

一、模型介绍

1、模型框架介绍

2、训练策略

3、似然函数模型

 4、损失函数

二、论文精华

1.尺度处理

三、仿真实验

1、数据集介绍

2、评价指标

2.1 评价指标1(分布式评估)

2.2 评价指标2(点预测评估)

2.3 定性分析

总结

---

前言

最近看论文《DeepAR：Probabilistic Forecasting with Autoregressive Recurrent Networks》收获良多，对于时间序列预测的理解又加深了，下面是我对这篇论文的解读

早期的时间序列预测主要模型是诸如ARIMA这样的单序列线性模型。这种模型对每个序列分别进行拟合。在ARIMA的基础上，又提出了引入非线性、引入外部特征等的优化。然而，ARIMA类模型在处理大规模时间序列时效率较低，并且由于每个序列分别独立拟合，无法共享不同序列存在的相似规律。深度学习模型在NLP、CV等领域取得了成功应用后，也被逐渐引入到解决时间序列预测问题中，常见的比如LSTM、CNN、ConvLSTM等。

传统预测算法解决不了两个问题：

1、联合多重时间序列。由于数据样本的不均衡导致了不同时间序列对于模型的影响程度是不同的，学习一个全局模型是很困难的；

拿商品销售为例（论文中举了亚马逊商品销售量的例子）

上图是亚马逊商品销售量的双对数直方图，近似一条直线，那么原曲线近似服从幂律分布（长尾分布），这种长尾分布对于模型的影响是巨大的，不均衡样本导致输入值的量级差异较大，大部分数据都是长尾分布（scale较小）的时间序列数据，就会导致模型的预测值偏向于长尾分布，而原来非长尾分布（scale较大）的时间序列将会受到影响，会出现明显的欠拟合，最后导致模型学习失败。对于这种尺度不一致的时间序列数据，通常的处理方式是使用标准化，将数据统一到同一个scale。在模型中，也可以通过Batch Normalization 层进行batch的标准化，但是在正计数数据（比如商品销量）中不是很有效。

2、预测未来某一时刻的概率分布。在特定场景下，概率预测比单点预测更有意义，比如零售业，若已知商品未来销量的概率分布，可以运用运筹优化方法推算在不同业务目标下的最优采购量，从而辅助决策。

一、模型介绍

1、模型框架介绍

 Zi,t代表第i个时间序列在时间t时刻的销量数据，X代表所有的协变量，假设[1, t0−1]为已知销量的时间区间，[t0, T]为需要预测的时间区间，Xi,1:T横跨[1, t0−1]和[t0, T]两个时间区间。

模型的目标是对条件分布P（已知1:t0-1时刻的z和1:T的X条件下得到t0:T时刻的z的概率）建模，如式（1），Q是模型的联合分布，t0:T时刻的所有的P乘积，l是似然函数，Θ代表模型要预测的参数，h 是有LSTM组成的多层RNN的实现函数，hi,t是网络的隐层输出。

DeepAR模型采用的是自回归网络（autoregressive recurrent network），假定概率分布P可以写成式（2）的形式，第一个等号代表将原先的联合概率分布写成自回归的概率乘积的形式，第二个等号是将自回归概率用一个参数化后的似然函数表示，h(.)代表一个RNN，输入上一时刻的隐层输出和输入,以及时刻的协变量,可以得到该时刻的隐层输出,在通过神经网络θ(·)将转化为给定分布的参数（具体分布见下文），分布确定后，就可以计算出似然的值。

将自回归过程放到sequence-to-sequence框架中：首先用encoder网络对1：t0-1的数据编码，得到隐层输出,再将其作为decoder网络的初始化输入，进行迭代输出的转化为分布的参数，这样就可以通过DeepAR得到预测的概率分布。

2、训练策略

 从论文中这一段可以看出，得到预测输出的过程是:在模型训练完成后，将t ，再使用祖先采样得到预测结果，对于t0~T的数据，在每一个时间步随机采样得到~,作为下一时间步的输入。重复该过程，得到一系列t0~T的采样值，并利用这些采样值可以计算所需的目标值，如分位数、期望等。

在训练过程中，使用Teacher Forcing策略，训练过程中有一定概率使用真实值，预测过程中不使用真实值，退化为普通的recursive seq2seq。

3、似然函数模型

~

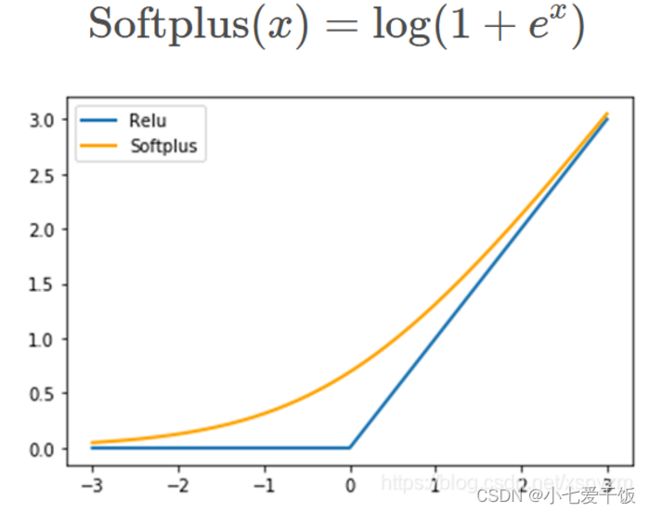
 DeepAR预测下一个时间点的概率分布的所有参数 θ（例如均值和方差）。论文中有两种选择，针对连续型数据（real-valued data，比如温度）的高斯似然和针对正计数数据（positive count data，比如销量）的负二项似然（negative-binomial likehood，负二项分布）。我们使用其均值和标准差 θ = ( µ , σ ) 对高斯似然进行参数化，其中均值由网络输出的仿射函数给出，为了确保 σ > 0，标准差通过应用仿射变换和 Softplus 激活函数获得， Softplus函数可以看作是ReLU函数的平滑。

 下图是Softplus和Relu对比图

 

 4、损失函数

模型参数可以通过最大化对数似然来学习，使用随机梯度下降求解：由于hi,t是输入的确定性函数，因此计算（10）所需的所有量都被观察到：

  由于模型的自回归性质，优化 (10) 导致模型在训练期间与从模型获得预测结果时的差异。在训练期间，zi,t 的值是已知的，使用teacher forcing策略；在预测过程中，对于 t ≥ t0，zi,t是未知的，并且预测样本服从分布  ~，根据 (3) 计算 hi,t，在解码器阶段不断递归得到预测输出，按理说应该会因为递归产生较大的累积误差，例如NLP 任务，但作者在预测中没有观察到由此产生的不利影响。NLP任务比如机器翻译，有上下文语境，如果一个环节翻译错了，后面的可能都会错掉，所以对这个要求比较高，但时序数据可能没有那么严格。

二、论文精华

1.尺度处理

将模型应用于幂律数据存在两个挑战：

DeepAR是一个全局模型，可以处理所有scale（尺度）的数据，这个尺度就是数据的数量级，那对于幂律数据是怎么处理的呢？论文中给出两步处理方法。

首先，由于模型的自回归性质，输入zi,t-1以及网络的输出（例如μ）都直接与观测值zi,t成比例，但两者间的网络非线性具有有限操作范围，网络因此必须学会将输入适当缩放，再在输出处翻转缩放。

而对于这种样本量级差异的解决方法，需要对商品销售量进行缩放，找到一个scale因子，对应到神经网络中，即输入到神经网络前除以v, 输出后乘以v。如何选择为每一个商品选择对应的v是一个挑战，实践发现使用商品的历史销量均值是一个不错的选择。

下面的式11和12是对负二项似然函数的参数进行的缩放变换，这里逆变换并不都是乘以vi

其次，由于数据的不平衡，均匀随机选择训练实例的随机优化过程，会很少访问大规模的小数时间序列，导致这些时间序列的拟合不足。为了抵消这种影响，在训练期间对样本进行weighted sampling scheme。文中加权采样方案中，从尺度为νi的示例中选择窗口的概率与 νi成正比。

三、仿真实验

1、数据集介绍

---

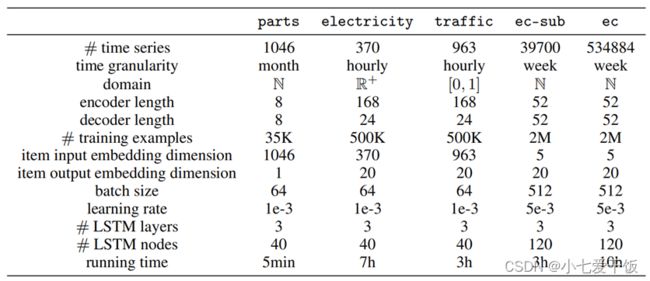
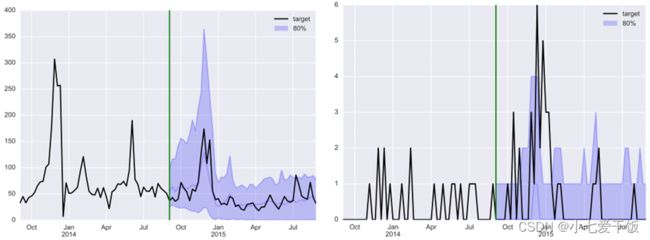
 DeepAR模型大概每秒可以训练14条时间序列，文中使用 MXNet 实现模型，并使用包含 4 个 CPU 和 1 个 GPU 的单个 p2.xlarge AWS 实例来运行所有实验。在此硬件上，可以在不到 10 小时内完成在包含 500K 时间序列的大型 ec 数据集上运行的完整训练和预测，如果还想更快的速度，可以并行运行。实验中用了5个数据集，包含公共数据集parts、electricity和traffic，以及亚马逊销量数据集ec和ec-sub。

 

 上图是在ec数据集上做的时间序列预测，可以看出模型不仅可以预测未来的数值，还可以对其不确定性做出估计

2、评价指标

2.1 评价指标1(分布式评估)

 ρ-risk指标，使用加权分位数损失评估预测分布的准确度

使用ρ-risk指标((quantile loss分位数损失) 量化预测分布的分位数ρ 的准确性，其中（L,S）代表在分界点t0之后的[L,L+S）时间范围，例如（2,1）代表[t0+2,t0+2+1)的时间范围，只度量这个范围内模型的结果。

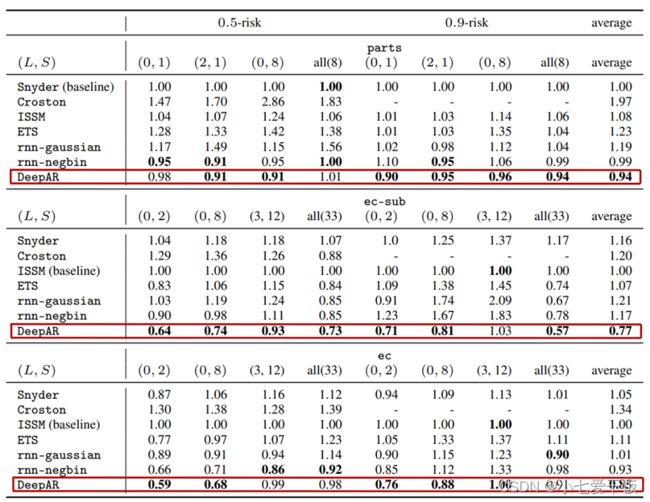
parts、ec、ec-sub数据集上的仿真实验，Croston、 ETS、 Snyder和ISSM都是文献中的方法，还有两个RNN模型；

rnn-gaussian ：模型架构与DeepAR相同，但使用统一采样和更简单的缩放机制，时间序列zi除以vi，输出乘以vi；

rnn-negbin： 使用负二项分布，统一采样且不缩放输入和输出。

从表中得出几条结论：

1、因parts多条序列幅度没有显著差异（不呈现幂律分布），rnn-negbin和DeepAR效果差不多

2、 ec和ec-sub多条序列幅度显著差异（呈现幂律分布），DeepAR明显比rnn-negbin效果好

3、3个数据集都是count-valued数据，负二项分布效果都优于高斯分布

2.2 评价指标2(点预测评估)

用真值和预测的均值来计算

 

 比较了DeepAR和MatFact(matrix factorization technique)在electricity和traffic数据集上的点预测精度，评价指标采用归一化偏差Normalized Deviation(ND)和归一化RMSE。结果表明，DeepAR在两个数据集上的性能都优于MatFact。

2.3 定性分析

  ISSM和DeepAR模型的不确定性随时间的推移而增长

展示了在ec数据集上的DeepAR和ISSM的边际预测分布的不同分位数的总和。与ISSM模型相比，不确定性的线性增长是建模假设的一部分，不确定性的增长模式是从数据中学习出来的。在这种情况下，该模型确实学习到了不确定性随时间的总体增长。然而，这并不是简单的线性增长：不确定性（正确地）在第四季度增加，不久之后又再次下降。所以DeepAR更好地学习到时序的不确定性。

        DeepAR与ISSM在分布预测的表现

显示了预测概率分布的好坏（预测准确度），其中percentile是真实分位数，coverage是预测覆盖量（横坐标可以认为是预测值，纵坐标可以认为是真实值）。若预测跟真实分布一致，则为灰色对角线。我们能看到DeepAR更靠近灰线，说明它概率分布预测最好。

总结

DeepAR的核心是用循环神经网络（RNN）预测多重时间序列，能够从时间序列中学习到全局模型，比较适合包含几百个时间序列的中型数据集，相比于一般的RNN网络，有三点优势：

1、不是直接简单地输出一个确定的预测值，而是输出预测值的一个概率分布。计算损失函数时，采用的是分布损失(Distribution Loss)，当数据分布不是正态而是长尾分布或者其他分布时，可以选用更适合该分布的损失函数。可以让算法只考虑特定分位的损失，比如0.25分位，而且还可以评估出预测的不确定性和相关的风险；

2、处理不同时序scale不一致的问题，除了传统分组训练预测、Batch Normalization ，更符合时序特性的处理方法可以是：加入scale因子和使用scale因子做加权采样；

3、能够从数据中学习复杂的模式，例如随时间推移的季节性和不确定性的增长情况。而且该方法几乎不需要根据各种数据集进行超参数调整。