AI | 第3章 机器学习算法 - sklearn 回归、聚类算法

---

前言

参考资料：
《B站：黑马程序员3天快速入门python机器学习》
《机器学习实战：基于Scikit-Learn、Keras和TenserFlow 原书第2版》

仅供参考

---

1. 线性回归

1.1 概述

• 定义：线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式；
• 特点：只有一个自变量的情况称为单变量回归，大于一个自变量情况的叫做多元回归；
• 广义线性模型：自变量一次(线性关系) + 参数一次；
• 公式：w 为权重值（回归系数）；b 为偏置；

$$h(w)=w_1{x}_1+w_2{x}_2+...+b=w^{T}x+b$$

• 其中 w，x 可以理解成矩阵：$w=\left(\begin{array}{c}b\\ w_1\\ w_2\end{array}\right)$ ，$x=\left(\begin{array}{c}1\\ x_1\\ x_2\end{array}\right)$

1.2 线性回归的损失和优化原理

• 目标：使 w 权重值 与 b 偏置 尽可能接近实际，需要使误差（损失函数）尽可能小，即优化损失；
• 损失函数公式：y_i 为第i个训练样本的真实值；h(x_i) 为第i个训练样本特征值组合预测函数；又称最小二乘法；

$$J(\theta )=(h_w(x_1)-y_1{)}^2+(h_w(x_2)-y_2{)}^2+...+(h_w(x_m)-y_m{)}^2=\sum _{i=1}^m(h_w(x_i)-y_i{)}^2$$

• 线性回归经常使用的两种优化算法：

  • 目的：使损失尽可能小；
  • 正规方程：
    • 公式：$w=(X^{T}X{)}^{-1}{X}^{T}y$；
    • 理解：X 为特征值矩阵，y 为目标值矩阵。直接求到最好的结果；
    • 缺点：当特征过多过复杂时，求解速度太慢并且得不到结果；
  • 梯度下降：
    • 公式：
      • $w_1^{‘}:=w_1-\alpha \frac{\delta cost(w_0+w_1{x}_1)}{\delta w_1}$；
      • $w_0^{‘}:=w_0-\alpha \frac{\delta cost(w_0+w_1{x}_1)}{\delta w_1}$；
    • 理解：α 为学习速率，需要手动指定（超参数），α 旁边的整体表示方向。沿着这个函数下降的方向找，最后就能找到山谷的最低点，然后更新 W 值；
    • 使用：面对训练数据规模十分庞大的任务 ，能够找到较好的结果；

• 均方误差 - 回归性能评估：

  • 作用：评估 正规方程 和 梯度下降 的回归性能；
  • 公式：yi 为预测值， ̄y 为真实值；

$$MSE=\frac{1}{m}\sum _{i=1}^m(y^i-\overline{y}{)}^2$$

1.3 线性回归 API

• 正规方程：
  • sklearn.linear_model.LinearRegression(fit_intercept=True)；
  • fit_intercept：是否计算偏置；
  • LinearRegression.coef_：回归系数；
  • LinearRegression.intercept_：偏置；

*Code1 正规方程代码示例

def linear_egression_demo():
    # 1.获取数据
    boston = load_boston()
    print("特征数量：\n", boston.data.shape)
    # 2.划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)
    # 3.标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    # 4.预估器
    estimator = LinearRegression()
    estimator.fit(x_train, y_train)
    # 5.得出模型
    print("正规方程权重值为：\n", estimator.coef_)
    print("正规方程偏置为：\n", estimator.intercept_)
    # 6.模型评估
    y_predict = estimator.predict(x_test)
    error = mean_squared_error(y_test, y_predict)
    print("预测房价：\n", y_predict)
    print("正规方程-均方误差为：\n", error)
    return None

• 梯度下降：
  • sklearn.linear_model.SGDRegressor(loss="squared_loss", fit_intercept=True, learning_rate ='invscaling', eta0=0.01)；
  • SGDRegressor 类实现了随机梯度下降学习，它支持不同的 loss 函数和正则化惩罚项来拟合线性回归模型；
  • loss：损失类型；
    • loss=”squared_loss”：普通最小二乘法；
  • fit_intercept：是否计算偏置；
  • learning_rate：string, optional；
    • 学习率填充；
    • ‘constant’: eta = eta0
    • ‘optimal’：eta = 1.0 / (alpha * (t + t0)) [default]
    • ‘invscaling’：eta = eta0 / pow(t, power_t)
      • power_t=0.25:存在父类当中；
    • 对于一个常数值的学习率来说，可以使用 learning_rate=’constant’ ，并使用 eta0 来指定学习率；
  • SGDRegressor.coef_：回归系数；
  • SGDRegressor.intercept_：偏置；

*Code2 梯度下降代码示例

def sGD_regressor_demo():
    # 1.获取数据
    boston = load_boston()
    # 2.划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)
    # 3.标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    # 4.预估器
    estimator = SGDRegressor()
    estimator.fit(x_train, y_train)
    # 5.得出模型
    print("梯度下降重值为：\n", estimator.coef_)
    print("梯度下降偏置为：\n", estimator.intercept_)
    # 6.模型评估
    y_predict = estimator.predict(x_test)
    error = mean_squared_error(y_test, y_predict)
    print("预测房价：\n", y_predict)
    print("梯度下降-均方误差为：\n", error)
    return None

• 均方误差 - 回归性能评估：
  • sklearn.metrics.mean_squared_error(y_true, y_pred)；
    • 均方误差回归损失；
    • y_true：真实值；
    • y_pred：预测值；
    • return：浮点数结果；

1.4 正规方程和梯度下降对比

	正规方程	梯度下降
学习率	不需要	需要
是否迭代	一次运算得出	迭代求解
应用	需要计算方程，时间复杂度高O(n3	特征数量较大可以使用

• 选择：
  • 小规模数据：
    • LinearRegression(不能解决拟合问题)；
    • 岭回归；
  • 大规模数据：SGDRegressor；

1.5 梯度下降的优化方法

• 拓展 - 关于优化方法 GD、SGD、SAG；
  • GD：
    • 梯度下降(Gradient Descent)，原始的梯度下降法需要计算所有样本的值才能够得出梯度，计算量大，所以后面才有会一系列的改进；
  • SGD：
    • 随机梯度下降(Stochastic gradient descent)是一个优化方法。它在一次迭代时只考虑一个训练样本；
      • 优点：
        • 高效；
        • 容易实现；
      • 缺点：
        • SGD 需要许多超参数：比如正则项参数、迭代数；
        • SGD 对于特征标准化是敏感的；
  • SAG：
    • 随机平均梯度法(Stochasitc Average Gradient)，由于收敛的速度太慢，有人提出 SAG 等基于梯度下降的算法；
    • Scikit-learn：SGDRegressor、岭回归、逻辑回归等当中都会有 SAG 优化；

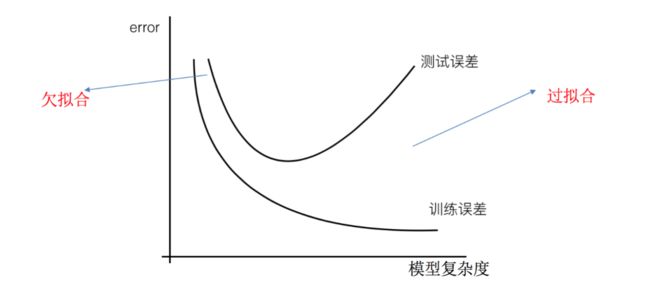
2. 欠拟合与过拟合

2.1 概述

• 定义：
  • 欠拟合：一个假设在训练数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单。训练集表现不好，测试集表现不好)
  • 过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合， 但是在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。(模型过于复杂。训练集表现好，测试集表现不好）；
    

2.2 原因及解决方法

• 欠拟合 原因以及解决办法：
  • 原因：学习到数据的特征过少；
  • 解决办法：增加数据的特征数量；
• 过拟合 原因以及解决办法：
  • 原因：原始特征过多，存在一些嘈杂特征， 模型过于复杂是因为模型尝试去兼顾各个测试数据点；
  • 解决办法：正则化，尽量减少高次项特征的影响；（在这里针对回归，我们选择了正则化。但是对于其他机器学习算法如分类算法来说也会出现这样的问题，除了一些算法本身作用之外（决策树、神经网络），我们更多的也是去自己做特征选择，包括之前说的删除、合并一些特征）

2.2.1 正则化

• L2 正则化：
  • 作用：可以使得其中一些 w 的都很小，都接近于 0，削弱某个特征的影响；
  • 优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象；
  • Ridge 回归 - 岭回归；
  • 优化后的损失函数 = 损失函数 + 惩罚系数 * 惩罚项；
    $$J(w)=\frac{1}{2m}\sum _{i=1}^m(h_w(x_i)-y_i{)}^2+\lambda \sum _{j=1}^n{w}_j^2$$
• L1 正则化：
  • 作用：可以使得其中一些 w 的值直接为 0，删除这个特征的影响；
  • LASSO 回归；
  • 优化后的损失函数 = 损失函数 + 惩罚系数 * 惩罚项；
    $$J(w)=\frac{1}{2m}\sum _{i=1}^m(h_w(x_i)-y_i{)}^2+\lambda \sum _{j=1}^n|w_j|$$
• 扩展：
  • 线性回归的损失函数用最小二乘法，等价于当预测值与真实值的误差满足正态分布时的极大似然估计；岭回归的损失函数，是最小二乘法+L2范数，等价于当预测值与真实值的误差满足正态分布，且权重值也满足正态分布（先验分布）时的最大后验估计；LASSO 的损失函数，是最小二乘法+L1范数，等价于等价于当预测值与真实值的误差满足正态分布，且且权重值满足拉普拉斯分布（先验分布）时的最大后验估计；

3. 线性回归的改进 - 岭回归 - Ridge 回归

3.1 概述

• 定义：岭回归，其实也是一种线性回归。只不过在算法建立回归方程时候，加上正则化的限制，从而达到解决过拟合的效果。即：带有L2正则化的线性回归；

• 公式：
  $$J(w)=\frac{1}{2m}\sum _{i=1}^m(h_w(x_i)-y_i{)}^2+\lambda \sum _{j=1}^n{w}_j^2$$

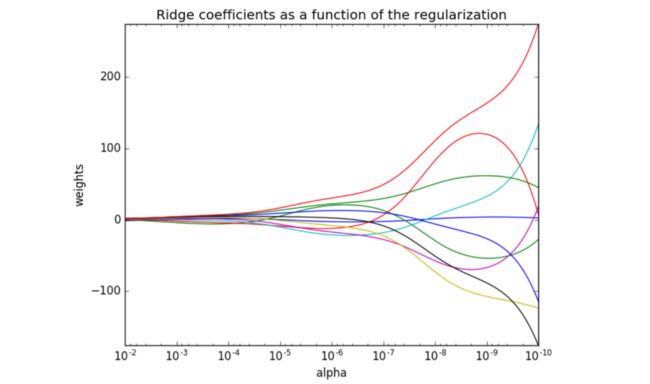
• λ 正则化力度 对 结果 的影响：

  • 正则化力度越大，权重系数会越小；
  • 正则化力度越小，权重系数会越大；

3.2 应用

• API：sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)
  • 具有 l2 正则化的线性回归；
  • alpha：正则化力度，惩罚项系数，也叫 λ；
    • λ 取值：0~1 1~10；
  • solver：会根据数据自动选择优化方法；
    • SAG：如果数据集、特征都比较大，选择该随机梯度下降优化；
  • normalize：数据是否进行标准化；
    • normalize=False：可以在 fit 之前调用preprocessing.StandardScaler 标准化数据；
  • Ridge.coef_：回归权重；
  • Ridge.intercept_：回归偏置；
• Ridge 方法相当于 SGDRegressor(penalty=‘l2’, loss=“squared_loss”)，只不过 SGDRegressor 实现了一个普通的随机梯度下降学习，推荐使用 Ridge(实现了 SAG)；

*Code3 岭回归代码示例

def ridge_demo():
    # 1.获取数据
    boston = load_boston()
    # 2.划分数据集
    x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)
    # 3.标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    # 4.预估器
    estimator = Ridge()
    estimator.fit(x_train, y_train)
    # 5.得出模型
    print("岭回归重值为：\n", estimator.coef_)
    print("岭回归偏置为：\n", estimator.intercept_)
    # 6.模型评估
    y_predict = estimator.predict(x_test)
    error = mean_squared_error(y_test, y_predict)
    print("预测房价：\n", y_predict)
    print("岭回归-均方误差为：\n", error)
    return None

4. 分类算法 - 逻辑回归与二分类

4.1 概述

• 定义：逻辑回归（Logistic Regression）是机器学习中的一种分类模型，逻辑回归是一种分类算法，虽然名字中带有回归，但是它与回归之间有一定的联系。由于算法的简单和高效，在实际中应用非常广泛；
• 应用场景：
  • 广告点击率 - 是否点击；
  • 是否为垃圾邮件；
  • 是否患病；
  • 金融诈骗 - 是否金融诈骗；
  • 虚假账号 - 是否虚假账；

4.2 逻辑回归的原理

• 输入公式：逻辑回归的输入就是一个线性回归的结果；

$$h(w)=w_1{x}_1+w_2{x}_2+...+b$$

• 激活函数公式：sigmoid 函数

  • 回归的结果输入到 sigmoid 函数当中，h(w)=θ^Tx；
  • 输出结果：[0, 1] 区间中的一个概率值，默认为 0.5 为阈值；
    $$g({\theta }^{T}x)=\frac{1}{1+e^{-{\theta }^{T}x}}$$

• 损失以及优化：逻辑回归的损失，称之为：对数似然损失；

  • 优化：同样使用梯度下降优化算法，去减少损失函数的值。这样去更新逻辑回归前面对应算法的权重参数，提升原本属于 1 类别的概率，降低原本是 0 类别的概率；
    $$cost(h_{\theta }(x),y)=\{\begin{array}{l}-log(h_{\theta }(x)),y=1\\ -log(1-h_{\theta }(x)),y=0\end{array}$$

• 综合完整损失函数：
  $$cost(h_{\theta }(x),y)=\sum _{i=1}^m(-y_{i}log(h_{\theta }(x))-(1-y_i)log(1-h_{\theta }(x)))$$

4.3 应用

• API：sklearn.linear_model.LogisticRegression(solver='liblinear', penalty=‘l2’, C = 1.0)
  • solver：优化求解方式（默认开源的 liblinear 库实现，内部使用了坐标轴下降法来迭代优化损失函数）
    • sag：根据数据集自动选择，随机平均梯度下降；
  • penalty：正则化的种类；
  • C：正则化力度；
• 默认将类别数量少的当做正例；
• LogisticRegression 方法相当于 SGDClassifir(loss=“log”, penalty=" ")，SGDClassifier 实现了一个普通的随机梯度下降学习，也支持平均随机梯度下降法（ASGD），可以通过设置average=True。而使用 LogisticRegression(实现了 SAG)；

*Code4 逻辑回归代码示例

# 4.特征工程
# 4.1 进行标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 5.预估器流程
# 使用逻辑回归
estimator = LogisticRegression()
estimator.fit(x_train, y_train)
print("得出来的权重：", estimator.coef_)
# 预测类别
print("预测的类别：", estimator.predict(x_test))
# 得出准确率
print("预测的准确率:", estimator.score(x_test, y_test))

4.4 分类的评估方法

4.4.1 精确率 与 召回率

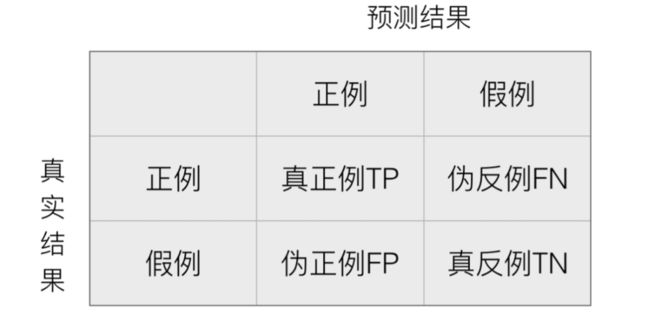
• 混淆矩阵：在分类任务下，预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合，构成混淆矩阵(适用于多分类)；

• 精确率：预测结果为正例样本中真实为正例的比例；
  • $P=\frac{TP}{TP+FP}$；
• 召回率：真实为正例的样本中预测结果为正例的比例（查的全，对正样本的区分能力）；
  • 用于严格估计；
  • $TPR=\frac{TP}{TP+FN}$；
• F1-score：反映了模型的稳健型；
  • $F1=\frac{2TP}{2TP+FN+FP}$；
• 以上指标不能衡量样本不均衡下的情况；
• 分类评估报告 API：
  • sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names=None )
    • y_true：真实目标值；
    • y_pred：估计器预测目标值；
    • labels:指定类别对应的数字；
    • target_names：目标类别名称；
    • return：每个类别精确率与召回率；

*Code5 精确率 与 召回率代码示例

# 6.查看精确率、召回率、F1-score
y_predict = estimator.predict(x_test)
report = classification_report(y_test, y_predict, labels=[2,4], target_names=["良性","恶性"])
print("精确率、召回率、F1-score：\n", report)

4.4.2 ROC曲线 与 AUC指标

• TPR 与 FPR：
  • $TPR=\frac{TP}{TP+FN}$；（召回率，下图纵坐标）
  • $FPR=\frac{FP}{FP+TN}$；（下图横坐标）
• 作用：衡量样本不均衡下的评估，即：真例 >> 假例；
• ROC曲线：
  • ROC曲线的横轴就是 FPRate，纵轴就是 TPRate，当二者相等时，表示的意义则是：对于不论真实类别是 1 还是 0 的样本，分类器预测为1的概率是相等的，此时 AUC 为 0.5；

• AUC指标：
  • AUC 的概率意义是随机取一对正负样本，正样本得分大于负样本的概率；
  • AUC 只能用来评价二分类。AUC 非常适合评价样本不平衡中的分类器性能；
  • AUC 的最小值为 0.5，最大值为 1，取值越高越好；
  • AUC=1，完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器；
  • 0.5
  • 最终 AUC 的范围在 [0.5, 1] 之间，并且越接近 1 越好；
• API：sklearn.metrics.roc_auc_score(y_true, y_score)
  • 计算 ROC曲线面积，即 AUC值；
  • y_true：每个样本的真实类别，必须为 0 (反例)，1 (正例)标记；
  • y_score：每个样本预测的概率值；

*Code6 AUC指标代码示例

# 7.AUC指标
# 将 y_test 转换成 0,1
y_true = np.where(y_test > 3, 1, 0)
auc = roc_auc_score(y_true, y_predict)
print("auc 指标：\n", auc)

5. 模型保存和加载

5.1 概述

• 当训练或者计算好一个模型之后，那么如果别人需要我们提供结果预测，就需要保存模型（主要是保存算法的参数）;
• API：import joblib
  • 保存：joblib.dump(rf, 'test.pkl')；
  • 加载：estimator = joblib.load('test.pkl')；

*Code7 模型保存和加载代码示例

# 5.1 保存模型
joblib.dump(estimator, "my_ridge.pkl")

# 5.2 加载模型
estimator = joblib.load("my_ridge.pkl")

6. 无监督学习 - K-means算法

6.1 概述

• 无监督学习是从无标签的数据开始学习的；
• 无监督学习包含的算法：
  • 聚类：K-means(K均值聚类)；
  • 降维：PCA；
• 特点：采用迭代式算法，直观易懂并且非常实；
• 缺点：容易收敛到局部最优解(可以通过 多次聚类 解决)；
• 应用场景：没有目标值，即：聚类一般做在分类之前；

6.2 K-means 原理

• K-means 聚类步骤：
  1. 随机设置 K (超参数)个特征空间内的点作为初始的聚类中心；
  2. 对于其他每个点计算到 K 个中心的距离，未知的点选择最近的一个聚类中心点作为标记类别；
  3. 接着对着标记的聚类中心之后，重新计算出每个聚类的新中心点（平均值）；
  4. 如果计算得出的新中心点与原中心点一样（或者相近），那么结束，否则重新进行第二步过程；

• API：sklearn.cluster.KMeans(n_clusters=8,init=‘k-means++’)
  • k-means 聚类；
  • n_clusters：开始的聚类中心数量；
  • init：初始化方法，默认为 'k-means ++’；
  • labels_：默认标记的类型，可以和真实值比较（不是值比较）；

*Code8 k-means代码示例

# 4、主成分分析的方法进行降维
# 1）实例化一个转换器类PCA
transfer = PCA(n_components=0.95)
# 2）fit_transform
data_new = transfer.fit_transform(table)
print("保留95%的信息，降维结果为：\n", data_new)
print(data_new.shape)

# 5. kmeans 算法
estimator = KMeans(n_clusters=3)
estimator.fit(data_new)
y_predict = estimator.predict(data_new)
print("查看前 300 个数据：\n", y_predict[:300])

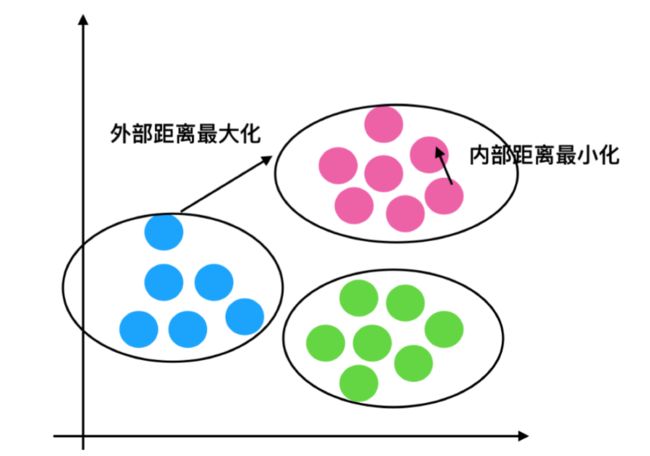
6.3 k-means 性能评估指标

• 轮廓系数:
  • 公式：对于每个点 i 为已聚类数据中的样本 ，b_i 为 i 到其它族群的所有样本的距离最小值，a_i 为 i 到本身簇的距离平均值。最终计算出所有的样本点的轮廓系数平均值；

$$S{C}_i=\frac{b_i-a_i}{max(b_i,a_i)}$$

• 轮廓系数数值分析：
  • 怎样才算好效果：外部距离最大化，内部距离最小化；
  • 数值化后：如果 b_i>>a_i：趋近于 1 效果越好， b_i<i：趋近于 -1，效果不好。轮廓系数的值是介于 [-1,1] ，越趋近于 1 代表内聚度和分离度都相对较优；
  • 分析：（以一个 蓝1 点为例）
    1. 计算出蓝1离本身族群所有点的距离的平均值 a_i；
    2. 蓝1 到其它两个族群的距离计算出平均值红平均，绿平均，取最小的那个距离作为 b_i 根据公式：极端值考虑：如果 b_i >> a_i：那么公式结果趋近于 1；如果 a_i >>> b_i：那么公式结果趋近于 -1；
       
• 轮廓系数 API：sklearn.metrics.silhouette_score(X, labels)
  • 计算所有样本的平均轮廓系数；
  • X：特征值；
  • labels：被聚类标记的目标值；

*Code9 k-means性能评估代码示例

# 6. 评估指标
score = silhouette_score(data_new, y_predict)
print("轮廓系数：\n", score)

---

最后

新人制作，如有错误，欢迎指出，感激不尽！ 如需转载，请标注出处！