支持向量机的原理与实践
目录
学习目标
支持向量机原理简介
支持向量
线性可分
最大间隔超平面
支持向量
SVM 最优化问题
SVM 优化
软间隔
解决问题
优化目标及求解
核函数
线性不可分
核函数的作用
常见核函数
SVM 有什么优缺点?
SVM 为什么采用间隔最大化(与感知机的区别)?
为什么要引入核函数?
如何选择核函数?
为什么SVM对缺失数据敏感?
LR与SVM的异同是什么?
为什么要把原问题转化为对偶问题?
KKT限制条件有哪些?
Demo实践
SVM基础知识的直观感受
支持向量机
软间隔
超平面
scikit-learn 中的 SVM
学习目标
- 了解支持向量机的理论
- 掌握支持向量机的 sklearn 函数调用
支持向量机原理简介
支持向量机(Support Vector Machine,SVM)是一个非常优雅的算法,具有非常完善的数学理论,常用于数据分类,也可以用于数据的回归预测中,由于其优美的理论保证和利用核函数对于线性不可分问题的处理技巧, 在上世纪90年代左右,SVM 曾红极一时。
SVM 是一种二类分类模型。它的基本思想是在特征空间中寻找间隔最大的分离超平面使数据得到高效的二分类,具体来讲,有三种情况(不加核函数的话就是个线性模型,加了之后才会升级为一个非线性模型):
- 当训练样本线性可分时,通过硬间隔最大化,学习一个线性分类器,即线性可分支持向量机;
- 当训练数据近似线性可分时,引入松弛变量,通过软间隔最大化,学习一个线性分类器,即线性支持向量机;
- 当训练数据线性不可分时,通过使用核技巧及软间隔最大化,学习非线性支持向量机。
支持向量
线性可分
在二维空间上,两类点被一条直线完全分开叫做线性可分。
严格的数学定义是:
![]() 和
和![]() 是 n 维欧氏空间中的两个点集。如果存在 n 维向量 w 和实数 b,使得所有属于
是 n 维欧氏空间中的两个点集。如果存在 n 维向量 w 和实数 b,使得所有属于![]() 的点
的点![]() 都有
都有![]() ,而对于所有属于
,而对于所有属于![]() 的点
的点![]() 则有
则有![]() ,则我们称
,则我们称![]() 和
和![]() 线性可分。
线性可分。
最大间隔超平面
从二维扩展到多维空间中时,将![]() 和
和![]() 完全正确地划分开的
完全正确地划分开的![]() 就成了一个超平面。
就成了一个超平面。
为了使这个超平面更具鲁棒性,我们会去找最佳超平面,以最大间隔把两类样本分开的超平面,也称之为最大间隔超平面。
- 两类样本分别分割在该超平面的两侧;
- 两侧距离超平面最近的样本点到超平面的距离被最大化了。
支持向量
样本中距离超平面最近的一些点(如上图中带蓝边的点),这些点叫做支持向量。
SVM 最优化问题
SVM 想要的就是找到各类样本点到超平面的距离最远,也就是找到最大间隔超平面。任意超平面可以用下面这个线性方程来描述:
![]()
二维空间点![]() 到直线
到直线![]() 的距离公式是:
的距离公式是:
扩展到 n 维空间后,点![]() 到直线
到直线![]() 的距离为:
的距离为:
其中
如图所示,根据支持向量的定义我们知道,支持向量到超平面的距离为 d,其他点到超平面的距离大于 d。
于是我们有这样的一个公式:
稍作转化可以得到:
![]() 是正数,我们暂且令它为 1(之所以令它等于 1,是为了方便推导和优化,且这样做对目标函数的优化没有影响),故:
是正数,我们暂且令它为 1(之所以令它等于 1,是为了方便推导和优化,且这样做对目标函数的优化没有影响),故:
将两个方程合并,我们可以简写为:
![]()
至此我们就可以得到最大间隔超平面的上下两个超平面:
![]()
每个支持向量到超平面的距离可以写为:
由上述![]() 可以得到
可以得到![]() ,所以我们得到:
,所以我们得到:
最大化这个距离:
这里乘上 2 是为了后面推导,对目标函数没有影响。刚刚我们得到支持向量![]() ,所以我们得到:
,所以我们得到:
再做一个转换:
为了方便计算(去除![]() 的根号),我们有:
的根号),我们有:
所以得到的最优化问题是:
SVM 优化
我们已知 SVM 优化的主问题是:
那么求解线性可分的 SVM 的步骤为:
步骤 1:
构造拉格朗日函数:
步骤 2:
利用强对偶性转化:
![]()
现对参数 w 和 b 求偏导数:
得到:
我们将这个结果带回到函数中可得:
也就是说:
步骤 3:
由步骤 2 得:
我们可以看出来这是一个二次规划问题,问题规模正比于训练样本数,我们常用 SMO(Sequential Minimal Optimization) 算法求解。
SMO(Sequential Minimal Optimization),序列最小优化算法,其核心思想非常简单:每次只优化一个参数,其他参数先固定住,仅求当前这个优化参数的极值。我们来看一下 SMO 算法在 SVM 中的应用。
我们刚说了 SMO 算法每次只优化一个参数,但我们的优化目标有约束条件: ,没法一次只变动一个参数。所以我们选择了一次选择两个参数。具体步骤为:
,没法一次只变动一个参数。所以我们选择了一次选择两个参数。具体步骤为:
1.选择两个需要更新的参数![]() 和
和![]() ,固定其他参数。于是我们有以下约束:
,固定其他参数。于是我们有以下约束:
![]()
其中![]() ,由此可以得出
,由此可以得出![]() ,也就是说我们可以用
,也就是说我们可以用![]() 的表达式代替
的表达式代替![]() 。这样就相当于把目标问题转化成了仅有一个约束条件的最优化问题,仅有的约束是
。这样就相当于把目标问题转化成了仅有一个约束条件的最优化问题,仅有的约束是![]()
2.对于仅有一个约束条件的最优化问题,我们完全可以在![]() 上对优化目标求偏导,令导数为零,从而求出变量值
上对优化目标求偏导,令导数为零,从而求出变量值![]() ,然后根据
,然后根据![]() 求出
求出![]() 。
。
3.多次迭代直至收敛。
通过 SMO 求得最优解![]() 。
。
步骤 4 :
我们求偏导数时得到:
![]()
由上式可求得 w。
我们知道所有![]() 对应的点都是支持向量,我们可以随便找个支持向量,然后带入:
对应的点都是支持向量,我们可以随便找个支持向量,然后带入:![]() ,求出 b 即可。
,求出 b 即可。
两边同乘![]() ,得
,得![]() 。
。
因为![]() ,所以:
,所以:![]() 。
。
为了更具鲁棒性,我们可以求得支持向量的均值:
![]()
步骤 5:
w 和 b 都求出来了,我们就能构造出最大分割超平面:![]() 。
。
分类决策函数:![]()
其中![]() 为阶跃函数:
为阶跃函数:
将新样本点导入到决策函数中既可得到样本的分类。
软间隔
解决问题
在实际应用中,完全线性可分的样本是很少的,如果遇到了不能够完全线性可分的样本,我们应该怎么办?比如下面这个:
于是我们就有了软间隔,相比于硬间隔的苛刻条件,我们允许个别样本点出现在间隔带里面,比如:
![]()
我们允许部分样本点不满足约束条件:
![]()
为了度量这个间隔软到何种程度,我们为每个样本引入一个松弛变量![]() ,令
,令![]() ,且
,且![]() 。对应如下图所示:
。对应如下图所示:
优化目标及求解
增加软间隔后我们的优化目标变成了:
![]()
其中 C 是一个大于 0 的常数,可以理解为错误样本的惩罚程度,若 C 为无穷大,![]() 必然无穷小,如此一来线性 SVM 就又变成了线性可分 SVM;当 C 为有限值的时候,才会允许部分样本不遵循约束条件。
必然无穷小,如此一来线性 SVM 就又变成了线性可分 SVM;当 C 为有限值的时候,才会允许部分样本不遵循约束条件。
接下来我们将针对新的优化目标求解最优化问题:
步骤 1:
构造拉格朗日函数:
其中![]() 和
和![]() 是拉格朗日乘子,w、b 和
是拉格朗日乘子,w、b 和![]() 是主问题参数。
是主问题参数。
根据强对偶性,将对偶问题转换为:
![]()
步骤 2:
分别对主问题参数w、b 和![]() 求偏导数,并令偏导数为 0,得出如下关系:
求偏导数,并令偏导数为 0,得出如下关系:
将这些关系带入拉格朗日函数中,得到:
最小化结果只有![]() 而没有
而没有![]() ,所以现在只需要最大化
,所以现在只需要最大化![]() 即可:
即可:
我们可以看到这个和硬间隔的一样,只是多了个约束条件。
然后我们利用 SMO 算法求解得到拉格朗日乘子![]() 。
。
步骤 3 :
![]()
然后我们通过上面两个式子求出 w 和 b,最终求得超平面![]()
这边要注意一个问题,在间隔内的那部分样本点是不是支持向量?
我们可以由求参数 w 的那个式子可看出,只要![]() 的点都能够影响我们的超平面,因此都是支持向量。
的点都能够影响我们的超平面,因此都是支持向量。
核函数
线性不可分
我们刚刚讨论的硬间隔和软间隔都是在说样本的完全线性可分或者大部分样本点的线性可分。
但我们可能会碰到的一种情况是样本点不是线性可分的,比如:
这种情况的解决方法就是:将二维线性不可分样本映射到高维空间中,让样本点在高维空间线性可分,比如:
对于在有限维度向量空间中线性不可分的样本,我们将其映射到更高维度的向量空间里,再通过间隔最大化的方式,学习得到支持向量机,就是非线性 SVM。
我们用 x 表示原来的样本点,用![]() 表示 x 映射到新的特征空间后到新向量。那么分割超平面可以表示为:
表示 x 映射到新的特征空间后到新向量。那么分割超平面可以表示为:
![]()
对于非线性 SVM 的对偶问题就变成了:
可以看到与线性 SVM 唯一的不同就是:之前的![]() 变成了
变成了![]()
核函数的作用
我们不禁有个疑问:只是做个内积运算,为什么要有核函数呢?
这是因为低维空间映射到高维空间后维度可能会很大,如果将全部样本的点乘全部计算好,这样的计算量太大了。
但如果我们有这样的一核函数![]() ,
,![]() 与
与![]() 在特征空间的内积等于它们在原始样本空间中通过函数
在特征空间的内积等于它们在原始样本空间中通过函数![]() 计算的结果,我们就不需要计算高维甚至无穷维空间的内积了。
计算的结果,我们就不需要计算高维甚至无穷维空间的内积了。
举个例子:假设我们有一个多项式核函数:
![]()
带进样本点后:
而它的展开项是:
如果没有核函数,我们则需要把向量映射成:
然后再进行内积计算,才能与多项式核函数达到相同的效果。
可见核函数的引入一方面减少了我们计算量,另一方面也减少了我们存储数据的内存使用量。
常见核函数
线性核函数
![]()
多项式核函数
![]()
高斯核函数
这三个常用的核函数中只有高斯核函数是需要调参的。
SVM 有什么优缺点?
优点:
- 有严格的数学理论支持,可解释性强,不依靠统计方法,从而简化了通常的分类和回归问题;
- 能找出对任务至关重要的关键样本(即:支持向量);
- 由于 SVM 是一个凸优化问题,所以求得的解一定是全局最优而不是局部最优;
- 采用核技巧之后,可以处理非线性分类/回归任务;
- 最终决策函数只由少数的支持向量所确定,计算的复杂性取决于支持向量的数目,而不是样本空间的维数,这在某种意义上避免了“维数灾难”。
缺点:
- 训练时间长。当采用 SMO 算法时,由于每次都需要挑选一对参数,因此时间复杂度为
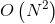 ,其中 N 为训练样本的数量;
,其中 N 为训练样本的数量; - 当采用核技巧时,如果需要存储核矩阵,则空间复杂度为
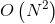 ;
; - 模型预测时,预测时间与支持向量的个数成正比。当支持向量的数量较大时,预测计算复杂度较高。
因此支持向量机目前只适合小批量样本的任务,无法适应百万甚至上亿样本的任务。
SVM 为什么采用间隔最大化(与感知机的区别)?
当训练数据线性可分时,存在无穷个分离超平面可以将两类数据正确分开。感知机利用误分类最小策略,求得分离超平面,不过此时的解有无穷多个。线性可分支持向量机利用间隔最大化求得最优分离超平面,这时,解是唯一的。另一方面,此时的分隔超平面所产生的分类结果是最鲁棒的,对未知实例的泛化能力最强。
为什么要引入核函数?
当样本在原始空间线性不可分时,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。而引入这样的映射后,在对偶问题的求解中,无需求解真正的映射函数,而只需要知道其核函数。核函数的定义:![]() ,即在特征空间的内积等于它们在原始样本空间中通过核函数 K 计算的结果。一方面数据变成了高维空间中线性可分的数据,另一方面不需要求解具体的映射函数,只需要给定具体的核函数即可,这样使得求解的难度大大降低。
,即在特征空间的内积等于它们在原始样本空间中通过核函数 K 计算的结果。一方面数据变成了高维空间中线性可分的数据,另一方面不需要求解具体的映射函数,只需要给定具体的核函数即可,这样使得求解的难度大大降低。
如何选择核函数?
- 当特征维数 d 超过样本数 m 时 (文本分类问题通常是这种情况),使用线性核函数;
- 当特征维数 d 比较小,样本数 m 中等时,使用RBF核函数;
- 当特征维数 d 比较小,样本数 m 特别大时,支持向量机性能通常不如深度神经网络。
为什么SVM对缺失数据敏感?
这里说的缺失数据是指缺失某些特征数据,向量数据不完整。SVM 没有处理缺失值的策略。而 SVM 希望样本在特征空间中线性可分,所以特征空间的好坏对 SVM 的性能很重要。缺失特征数据将影响训练结果的好坏。
LR与SVM的异同是什么?
异:
- LR 是参数模型,SVM 是非参数模型;
- 从目标函数来看,区别在于 LR 采用的是 logistical loss,SVM 采用的是 hinge loss。这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重;
- SVM 的处理方法是只考虑支持向量,也就是和分类最相关的少数点,去学习分类器。而 LR 通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重;
- LR 相对来说模型更简单,好理解,特别是大规模线性分类时比较方便。而 SVM 的理解和优化相对来说复杂一些,SVM 转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算;
- LR 能做的 SVM 能做,但可能在准确率上有问题,SVM能做的LR有的做不了。
同:
- LR 和 SVM 都可以处理分类问题,且一般都用于处理线性二分类问题(在改进的情况下可以处理多分类问题);
- 两个方法都可以增加不同的正则化项,如 L1、L2 等。因此在很多情况下,两种算法的结果是很接近的。
为什么要把原问题转化为对偶问题?
- 在转化为对偶问题之后,原问题中的不等式约束变为等式约束。
- 转化之后可以很方便的将核函数引入。
- 转化改变了问题的复杂度。
KKT限制条件有哪些?
对于一个具有等式和不等式约束的一般优化问题:
![]()
KKT 条件给出了判断![]() 是否为最优解的必要条件,即:
是否为最优解的必要条件,即:
Demo实践
首先我们利用 sklearn 直接调用 SVM 函数进行实践尝试。
- Step1:库函数导入
## 基础函数库
import numpy as np
## 导入画图库
import matplotlib.pyplot as plt
import seaborn as sns
## 导入支持向量机模型函数
from sklearn import svm- Step2:构建数据集并进行模型训练
##Demo演示SVC分类
## 构造数据集
x_fearures = np.array([[-1, -2], [-2, -1], [-3, -2], [1, 3], [2, 1], [3, 2]])
y_label = np.array([0, 0, 0, 1, 1, 1])
## 调用SVC模型 (支持向量机分类)
svc = svm.SVC(kernel='linear')
## 用SVM模型拟合构造的数据集
svc = svc.fit(x_fearures, y_label) - Step3:模型参数查看
## 查看其对应模型的w
print('the weight of SVC:', svc.coef_)
## 查看其对应模型的w0
print('the intercept(w0) of SVC:', svc.intercept_)
# the weight of SVC: [[ 0.33364706 0.33270588]]
# the intercept(w0) of SVC: [-0.00031373]- Step4:模型预测
## 模型预测
y_train_pred = svc.predict(x_fearures)
print('The predction result:', y_train_pred)
# The predction result: [0 0 0 1 1 1]- Step5:模型可视化
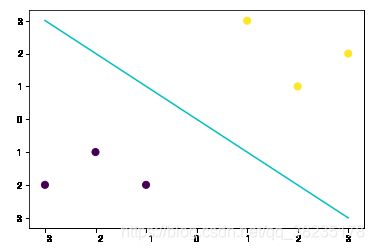
由于此处选择的线性核函数,所以在此我们可以将svm进行可视化。
# 最佳函数
x_range = np.linspace(-3, 3)
w = svc.coef_[0]
a = -w[0] / w[1]
y_3 = a * x_range - (svc.intercept_[0]) / w[1]
# 可视化决策边界
plt.figure()
plt.scatter(x_fearures[:, 0], x_fearures[:, 1], c=y_label, s=50, cmap='viridis')
plt.plot(x_range, y_3, '-c')
plt.show()可以对照逻辑回归模型的决策边界,我们可以发现两个决策边界是有一定差异的(可以对比两者在X,Y轴 上的截距),这说明这两个不同模型在相同数据集上找到的判别线是不同的,而这不同的原因其实是由于两者选择的最优目标是不一致的。
SVM基础知识的直观感受
支持向量机
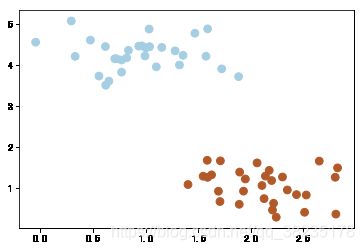
我们常常会碰到这样的一个问题,首先给你一些分属于两个类别的数据:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
%matplotlib inline
# 画图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=60, cmap=plt.cm.Paired)现在需要一个线性分类器,将这些数据分开来。
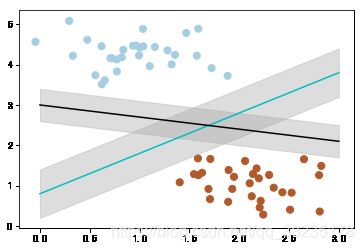
我们可能会有多种分法:
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
x_fit = np.linspace(0, 3)
# 画函数
y_1 = 1 * x_fit + 0.8
plt.plot(x_fit, y_1, '-c')
y_2 = -0.3 * x_fit + 3
plt.plot(x_fit, y_2, '-k')那么现在有一个问题,两个分类器,哪一个更好呢?
为了判断好坏,我们需要引入一个准则:好的分类器不仅仅是能够很好的分开已有的数据集,还能对未知数据集进行泛化性能高的划分。
假设,现在有一个属于红色数据点的新数据(3, 2.8)
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
plt.scatter([3], [2.8], c='#cccc00', marker='<', s=100, cmap=plt.cm.Paired)
x_fit = np.linspace(0, 3)
# 画函数
y_1 = 1 * x_fit + 0.8
plt.plot(x_fit, y_1, '-c')
y_2 = -0.3 * x_fit + 3
plt.plot(x_fit, y_2, '-k')![]()
可以看到,此时黑色的线会把这个新的数据集分错,而蓝色的线不会。
那么如何客观的评判两条线的健壮性呢?
此时,我们需要引入一个非常重要的概念:最大间隔。
最大间隔刻画着当前分类器与数据集的边界,以这两个分类器为例:
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
x_fit = np.linspace(0, 3)
# 画函数
y_1 = 1 * x_fit + 0.8
plt.plot(x_fit, y_1, '-c')
# 画边距
plt.fill_between(x_fit, y_1 - 0.6, y_1 + 0.6, edgecolor='none', color='#AAAAAA', alpha=0.4)
y_2 = -0.3 * x_fit + 3
plt.plot(x_fit, y_2, '-k')
plt.fill_between(x_fit, y_2 - 0.4, y_2 + 0.4, edgecolor='none', color='#AAAAAA', alpha=0.4)可以看到, 蓝色的线最大间隔是大于黑色的线的。
所以我们会选择蓝色的线作为我们的分类器。
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 画图
y_1 = 1 * x_fit + 0.8
plt.plot(x_fit, y_1, '-c')
# 画边距
plt.fill_between(x_fit, y_1 - 0.6, y_1 + 0.6, edgecolor='none', color='#AAAAAA', alpha=0.4)那么,我们现在的分类器是最优分类器吗?
或者说,有没有更好的分类器,它具有更大的间隔?
答案是有的。
为了找出最优分类器,我们需要引入:SVM
from sklearn.svm import SVC
# SVM 函数
clf = SVC(kernel='linear')
clf.fit(X, y)# 最佳函数
w = clf.coef_[0]
a = -w[0] / w[1]
y_3 = a * x_fit - (clf.intercept_[0]) / w[1]
# 最大边距 下届
b_down = clf.support_vectors_[0]
y_down = a * x_fit + b_down[1] - a * b_down[0]
# 最大边距 上届
b_up = clf.support_vectors_[-1]
y_up = a * x_fit + b_up[1] - a * b_up[0]# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 画函数
plt.plot(x_fit, y_3, '-c')
# 画边距
plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
# 画支持向量
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b', s=80, facecolors='none')带蓝边的点是距离当前分类器最近的点,我们称之为支持向量。
支持向量机为我们提供了在众多可能的分类器之间进行选择的原则,从而确保对未知数据集具有更高的泛化性。
软间隔
但很多时候,我们拿到的数据是这样子的:
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.9)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)这种情况并不容易找到这样的最大间隔。
于是我们就有了软间隔,相比于硬间隔而言,我们允许个别数据出现在间隔带中。
我们知道,如果没有一个原则进行约束,满足软间隔的分类器也会出现很多。
所以需要对分错的数据进行惩罚,SVC 函数中,有一个参数 C 就是惩罚参数。
惩罚参数越小,容忍性就越大。
以 C=1 为例子,比如说:
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.9)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 惩罚参数:C=1
clf = SVC(C=1, kernel='linear')
clf.fit(X, y)
x_fit = np.linspace(-1.5, 4)
# 最佳函数
w = clf.coef_[0]
a = -w[0] / w[1]
y_3 = a * x_fit - (clf.intercept_[0]) / w[1]
# 最大边距 下届
b_down = clf.support_vectors_[0]
y_down = a * x_fit + b_down[1] - a * b_down[0]
# 最大边距 上届
b_up = clf.support_vectors_[-1]
y_up = a * x_fit + b_up[1] - a * b_up[0]
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 画函数
plt.plot(x_fit, y_3, '-c')
# 画边距
plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
# 画支持向量
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b', s=80, facecolors='none')惩罚参数 C=0.2 时,SVM 会更具包容性,从而兼容更多的错分样本:
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.9)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 惩罚参数:C=0.2
clf = SVC(C=0.2, kernel='linear')
clf.fit(X, y)
x_fit = np.linspace(-1.5, 4)
# 最佳函数
w = clf.coef_[0]
a = -w[0] / w[1]
y_3 = a * x_fit - (clf.intercept_[0]) / w[1]
# 最大边距 下届
b_down = clf.support_vectors_[10]
y_down = a * x_fit + b_down[1] - a * b_down[0]
# 最大边距 上届
b_up = clf.support_vectors_[1]
y_up = a * x_fit + b_up[1] - a * b_up[0]
# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 画函数
plt.plot(x_fit, y_3, '-c')
# 画边距
plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
# 画支持向量
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b', s=80, facecolors='none')![]()
超平面
如果我们遇到这样的数据集,没有办法利用线性分类器进行分类:
from sklearn.datasets.samples_generator import make_circles
# 画散点图
X, y = make_circles(100, factor=.1, noise=.1, random_state=2019)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
clf = SVC(kernel='linear').fit(X, y)
# 最佳函数
x_fit = np.linspace(-1.5, 1.5)
w = clf.coef_[0]
a = -w[0] / w[1]
y_3 = a * X - (clf.intercept_[0]) / w[1]
plt.plot(X, y_3, '-c')我们可以将二维(低维)空间的数据映射到三维(高维)空间中。
此时,我们便可以通过一个超平面对数据进行划分。
所以,我们映射的目的在于使用 SVM 在高维空间找到超平面的能力。
from mpl_toolkits.mplot3d import Axes3D
# 数据映射
r = np.exp(-(X[:, 0] ** 2 + X[:, 1] ** 2))
ax = plt.subplot(projection='3d')
ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap=plt.cm.Paired)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
x_1, y_1 = np.meshgrid(np.linspace(-1, 1), np.linspace(-1, 1))
z = 0.01 * x_1 + 0.01 * y_1 + 0.5
ax.plot_surface(x_1, y_1, z, alpha=0.3)在 SVC 中,我们可以用高斯核函数来实现这以功能:kernel='rbf'
# 画图
X, y = make_circles(100, factor=.1, noise=.1, random_state=2019)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
clf = SVC(kernel='rbf')
clf.fit(X, y)
ax = plt.gca()
x = np.linspace(-1, 1)
y = np.linspace(-1, 1)
x_1, y_1 = np.meshgrid(x, y)
P = np.zeros_like(x_1)
for i, xi in enumerate(x):
for j, yj in enumerate(y):
P[i, j] = clf.decision_function(np.array([[xi, yj]]))
ax.contour(x_1, y_1, P, colors='k', levels=[-1, 0, 0.9], alpha=0.5, linestyles=['--', '-', '--'])
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b', s=80, facecolors='none');此时便完成了非线性分类。
scikit-learn 中的 SVM
SVC,NuSVC 和 LinearSVC 能在数据集中实现多元分类。
SVR,NuSVR 和 LinearSVR 能在数据集中实现回归。
使用诀窍
-
避免数据复制:对于 SVC, SVR, NuSVC 和 NuSVR, 如果数据是通过某些方法而不是用行优先存储(C-order)的双精度,那它会在调用底层的 C 命令前先被复制。 您可以通过检查它的 flags 属性,来确定给定的 numpy 数组是不是行优先存储(C-order)的。
对于 LinearSVC (和 LogisticRegression) 的任何输入,都会以 numpy 数组形式,被复制和转换为用 liblinear 内部稀疏数据去表达(双精度浮点型 float 和非零部分的 int32 索引)。 如果您想要一个适合大规模的线性分类器,又不打算复制一个密集的行优先存储(C-order)双精度 numpy 数组作为输入, 那我们建议您去使用 SGDClassifier 类作为替代。目标函数可以配置为和 LinearSVC 模型差不多相同的。
- 内核的缓存大小:在大规模问题上,对于 SVC,SVR,NuSVC 和 NuSVR,内核缓存的大小会特别影响到运行时间。如果您有足够可用的 RAM,不妨把它的缓存大小设得比默认的 200(MB) 要高,例如为 500(MB) 或者 1000(MB)。
-
惩罚系数 C 的设置:在合理的情况下, C 的默认选择为 1 。如果您有很多混杂的观察数据, 您应该要去调小它。 C 越小,就能更好地去正规化估计。
当 C 值较大时,LinearSVC和 LinearSVR 对 C 值较不敏感,即当 C 值大于特定阈值后,模型效果将会停止提升。同时,较大的 C 值将会导致较长的训练时间,Fan et al.(2008)的论文显示,训练时间的差距有时会达到10倍。
- 支持向量机算法本身不能够很好地支持非标准化的数据,所以强烈建议您将数据标准化。 举个示例,对于输入向量 X, 规整它的每个数值范围为 [0, 1] 或 [-1, +1] ,或者标准化它为均值为 0 方差为 1 的数据分布。请注意, 相同的缩放标准必须要应用到所有的测试向量,从而获得有意义的结果。
- 在 NuSVC / OneClassSVM / NuSVR 内的参数 nu , 近似是训练误差和支持向量的比值。
- 在 SVC 中,如果分类器的数据不均衡(例如,很多正例少于负例),设置 class_weight='balanced' 与/或尝试不同的惩罚系数 C 。
- 底层实现的随机性:SVC 和 NuSVC 的底层实现仅使用随机数生成器来打乱数据顺序进行概率估计(当 probability 被设置为 True 时)。这种随机性可以用 random_state 参数来控制。如果将 probability 设为 False,这些估计器就不是随机的, random_state 对结果没有影响。底层的 OneClassSVM 实现类似于 SVC 和 NuSVC 的实现。由于 OneClassSVM 没有提供概率估计,所以它不是随机的。 底层的 LinearSVC 实现使用随机数生成器来选择特征,当用双坐标下降(当 dual 被设置为 True )。因此,对于相同的输入数据,结果略有不同并不罕见。如果发生这种情况,尝试使用较小的 tol 参数。这种随机性也可以通过 random_state 参数来控制。当 dual 设置为 False 时,LinearSVC 的底层实现不是随机的,random_state 对结果没有影响。
- 使用由 LinearSVC(loss='l2', penalty='l1', dual=False) 提供的 L1 惩罚去产生稀疏解,也就是说,特征权重的子集不同于零,这样做有助于决策函数。 随着增加 C 会产生一个更复杂的模型(有更多的特征被选择)。可以使用 l1_min_c 去计算 C 的数值,去产生一个”null” 模型(所有的权重等于零)。


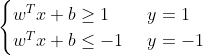


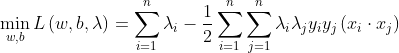





![\max_{\lambda } \left [ \sum_{i=1}^{n} \lambda _{i} - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \lambda _{i}\lambda _{j}y_{i}y_{j}\left ( x_{i}\cdot x_{j} \right ) \right ]](http://img.e-com-net.com/image/info8/0a20a39201ce4854b25efce783d7e60f.gif)