图的遍历（深度优先遍历DFS，广度优先遍历BFS）以及Ｃ语言的实现

遍历的定义：

从已给的连通图中某一顶点出发，沿着一些边访遍图中所有的顶点，且使每个顶点仅被访问一次，就叫做图的遍历，它是图的基本运算．

一:深度优先遍历（ＤＦＳ）

１，在访问图中某一起始顶点Ｖ后，由Ｖ出发，访问它的任一邻接顶点Ｗ１

２，再从Ｗ１出发，访问与Ｗ１邻接但还未被访问过的顶点Ｗ２；

３，然后再从Ｗ２出发，进行类似的访问．．．．．．

４，如此进行下去，直至到达所有的邻接顶点都被访问过的顶点Ｕ为止．

５，接着，退回一步，退到前一次刚访问过的顶点，看是否还有其它没有被访问过的邻接点

６，如果有，则访问此顶点，之后再从此顶点出发，进行与前述类似的访问；

７，如果没有，就再退回一步进行搜索．重复上述过程，直到连通图中所有顶点都被访问过为止．

１，使用邻接矩阵表示的无向图深度优先遍历的实现

 

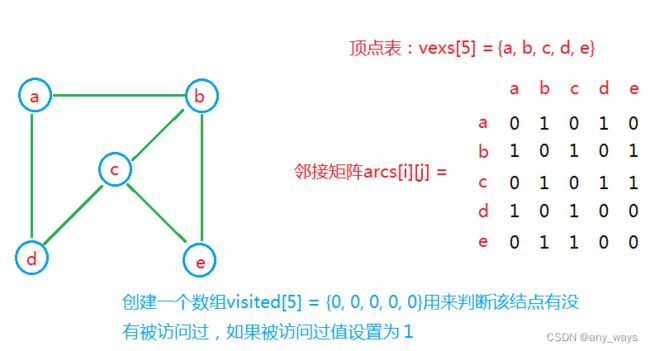
 以上图为例，以邻结矩阵创建无向图，并且深度优先遍历

#include 
#include 
#define MAXSIZE 100 //最大顶点数
#define MAX_INT 32767//设置最大值
typedef struct{
    char vexs[MAXSIZE];//这里的数据类型根据实际情况而定
    int arcs[MAXSIZE][MAXSIZE];//这里的数据类型根据实际情况而定
    int vexnum, arcnum;//图的当前顶点数和边数
}Graph;
int get_index(char* arr,char m)
{
    int i = 0;
    for(i = 0; i < MAXSIZE; i++)
    {
        if(arr[i] == m)return i;
    }
    return -1;
}

void CreatGraph(Graph* G)
{
    int i,j = 0;
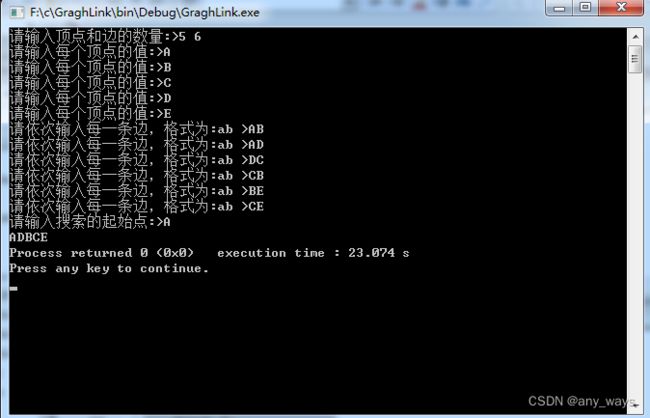
    printf("请输入顶点和边的数量:>");
    scanf("%d%d",&G->vexnum,&G->arcnum);//把输入的值保存到图结构体中
    for(i = 0; i < G->vexnum; i++)//初始化邻接矩阵
    {
        for(j = 0; j < G->vexnum; j++)
            {
                G->arcs[i][j] = 0;
            }

    }

    for(i = 0; i < G->vexnum; i++)
    {
        printf("请输入每个顶点的值:>");
        getchar();//清除键盘缓存区的回车键
        scanf("%c", &G->vexs[i]);//把输入的值保存到顶点数组当中
    }
    for(i = 0; i < G->arcnum; i++)//有几条边，循环几次
    {
        char m,n;//用来接收两个顶点
        int j,k;//接收顶点的下标
        printf("请依次输入每一条边，格式为:ab >");
        getchar();
        scanf("%c%c",&m,&n);
        j = get_index(G->vexs,m);//得到输入的m的值，在顶点数组中的下标
        k = get_index(G->vexs,n);//得到输入的n的值，在顶点数组中的下标
        G->arcs[j][k] = 1;//给邻接矩阵对应的位置赋权值
        G->arcs[k][j] = 1;//因为是无向网，所以是对称的，给对称点赋相同值
    }


}
//深度遍历创建的无向图
void DepthSearch(Graph G, int v, int*visited)//参数为创建的图，输入的值在数组中的下标，判断是否被访问过的数组
{
    int i = 0;
    visited[v] = 1;
    printf("%c", G.vexs[v]);
    for(i = 0; i < G.vexnum; i++)//遍历二维数组v行的每一列
    {
        if((G.arcs[v][i] == 1)&&(visited[i]!=1))//如果有边相连，而且该顶点还没有被访问过
            DepthSearch(G, i,visited);//递归搜索该顶点
    }
}
int main()
{
    Graph G;
    CreatGraph(&G);
    char input;
    int visited[MAXSIZE] = {0};//创建数组，用来判断某一个顶点是否被访问过
    printf("请输入搜索的起始点:>");
    getchar();
    scanf("%c",&input);
    DepthSearch(G, get_index(G.vexs, input),visited);
    return 0;

}

 ２，使用邻接表表示的无向图深度优先遍历的实现

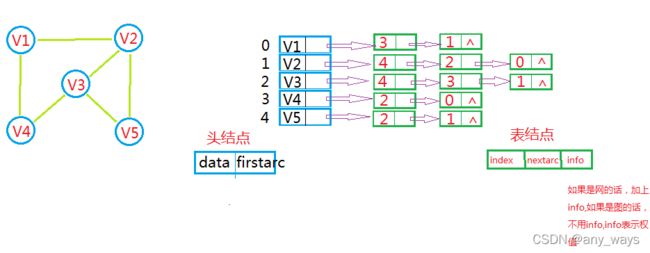
 同样以这个无向图为例：创建一个visited[]数组，用来判断某个顶点是否已经被访问过

代码与上面邻接矩阵也差不多，只是在条件判断时有所不同，这里不需要判断表结点是不是顶点的边，只需要判断表结点是不是空．具体代码如下：

#include 
#include 
#define MAXSIZE 100 //最大顶点数
#define MAX_INT 32767//设置最大值
typedef struct TableNode{//表结点
    int index;//结点在数组中的下标
    struct TableNode* nextarc;
    int info;//权值

}TNode;

typedef struct{//头结点
    char data;
    TNode* firstarc;
}HNode;

typedef struct{//整个无向网的结构体
    HNode* head;
    int vexnum,arcnum;
}Gragh;
int get_index(HNode* arr,char m)
{
    int i = 0;
    for(i = 0; i < MAXSIZE; i++)
    {
        if(arr[i].data == m)return i;
    }
    return -1;
}

void CreatGraph(Gragh* G)
{
    int i = 0;
    printf("请输入顶点和边的数量:>");
    scanf("%d%d",&G->vexnum,&G->arcnum);//把输入的值保存到图结构体中


    for(i = 0; i < G->vexnum; i++)
    {
        printf("请输入每个顶点的值:>");
        getchar();//清除键盘缓存区的回车键
        scanf("%c", &G->head[i].data);//把输入的值保存到顶点数组当中
        G->head[i].firstarc = NULL;
    }
    for(i = 0; i < G->arcnum; i++)//有几条边，循环几次
    {
        char m,n;//用来接收两个顶点
        int j,k;//接收顶点的下标
        printf("请依次输入每一条边，格式为:ab >");
        getchar();
        scanf("%c%c",&m,&n);
        j = get_index(G->head,m);//得到输入的m的值，在顶点数组中的下标
        k = get_index(G->head,n);//得到输入的n的值，在顶点数组中的下标
        TNode* P1 = malloc(sizeof(TNode));
        P1->index = k;
        P1->nextarc = G->head[j].firstarc;
        G->head[j].firstarc = P1;
        //因为是无向图，所以还要建立一条反向的边
        TNode* P2 = malloc(sizeof(TNode));
        P2->index = j;
        P2->nextarc = G->head[k].firstarc;
        G->head[k].firstarc = P2;
    }


}
//深度遍历创建的无向图
void DepthSearch(Gragh G, int v, int*visited)//参数为创建的图，输入的值在数组中的下标，判断是否被访问过的数组
{
    visited[v] = 1;
    printf("%c", G.head[v].data);
    TNode* P = G.head[v].firstarc;
    while(P)
    {
        if(!visited[P->index])DepthSearch(G, P->index, visited);//如果表结点不为空且判断数组值不为１，则递归搜索该结点
        P = P->nextarc;//指针指向该结点的下一个结点
    }

}
int main()
{
    Gragh G;
    CreatGraph(&G);
    char input;
    int visited[MAXSIZE] = {0};//创建数组，用来判断某一个顶点是否被访问过
    printf("请输入搜索的起始点:>");
    getchar();
    scanf("%c",&input);
    DepthSearch(G, get_index(G.head, input),visited);
    return 0;

}

二:广度优先遍历（ＢＦＳ） 

方法：从图的某一结点出发，首先依次访问该结点的所有邻接点，再按这些顶点被访问的先后次序依次访问与他们相邻接的所有未被访问的顶点，重复此过程，直至所有顶点均被访问为止．

根据广度优先的特点，和以前树的层次遍历比较相似，这里我们也采用队列的方式，把要访问的顶点先入队，访问完后，再出队，这样不停的循环，直到队列为空，就表示遍历完成了．

１，使用邻接矩阵表示的无向图广度优先遍历的实现

这里为了代码的简洁和可读性，我把常用的一些代码，创建无向图和队列，都放到头文件中去了

如果有需要，可以私信．创建无向图和队列的代码在前面的文章里都有．这里只是重点讲广度优先遍历的算法

#include 
#include 
#define MAXSIZE 10 //最大顶点数
#include "gragh.h"
//广度优先遍历创建的无向图
void BreadthSearch(Gragh G, int v, int*visited, SQ* Q)//参数为创建的图，输入的值在数组中的下标，判断是否被访问过的数组，以及队列
{
    visited[v] = 1;//把传入的起点，设置为１
    push_sq(Q, G.head[v]);//把传入的顶点入队

    while(Q->back != Q->front)//如果队不为空，则循环
    {
        printf("%c", Q->arr[Q->front].data);//访问队列最前面的数据
        TNode* P = Q->arr[Q->front].firstarc;//把指针指向顶点对应的第一个表结点
        while(P)//只要表结点不为空就循环
        {
            if(!visited[P->index])push_sq(Q, G.head[P->index]);//把没有访问过的顶点入队列
            visited[P->index] = 1;//把入了队列的顶点，在visited数组中设置为１
            P = P->nextarc;//指针指向下一条边
        }
        pop_sq(Q);
    }
}
int main()
{
    SQ Q;//队列类型变量
    Gragh G;//图类型变量
    CreatGraph(&G);//创建一个无向图
    InitSQ(&Q);//创建并初始化一个顺序队列
    char input;
    int visited[MAXSIZE] = {0};//创建数组，用来判断某一个顶点是否被访问过
    printf("请输入搜索的起始点:>");
    getchar();
    scanf("%c",&input);
    BreadthSearch(G, get_index(G.head, input),visited,&Q);//广度优先遍历无向图
    return 0;

}

邻接表不唯一，根据你创建算法，头插法，尾插法不同，而不同

邻接矩阵是唯一的，所以用邻接矩阵创建的图，遍历出来的结果都一样． 

邻接矩阵的广度遍历，和邻接表的差不多，这里就不详细说了！

_____________________________________

最近老是有人问我上面代码里.h和.c文件的内容，我现在发出来

gragh.h:

#include 
#include 
#define MAXSIZE 10 //最大顶点数
typedef struct TableNode{//表结点
    int index;//结点在数组中的下标
    struct TableNode* nextarc;
    int info;//权值
}TNode;

typedef struct{//头结点
    char data;
    TNode* firstarc;
}HNode;

typedef struct{//整个无向网的结构体
    HNode* head;
    int vexnum,arcnum;
}Gragh;
typedef struct SequenceQueue//定义一个队列类型结构体
{
    HNode* arr;//定义一个数组，类型自己决定
    int front;//队列头指针（下标）
    int back;//队列尾指针（下标）
}SQ;
int get_index(HNode* arr,char m);
void CreatGraph(Gragh* G);
void InitSQ(SQ* Q);//创建并初始化一个队列
void push_sq(SQ* Q, HNode e);//插入规则，从队尾插入
void pop_sq(SQ* Q);//删除规则，从队头删除
int length_sq(SQ* Q);

gragh.c:

#include 
#include 
#define MAXSIZE 10 //最大顶点数
#define MAX_INT 32767//设置最大值
#include "gragh.h"
int get_index(HNode* arr,char m)
{
    int i = 0;
    for(i = 0; i < MAXSIZE; i++)
    {
        if(arr[i].data == m)return i;
    }
    return -1;
}

void CreatGraph(Gragh* G)
{
    int i = 0;
    printf("请输入顶点和边的数量:>");
    scanf("%d%d",&G->vexnum,&G->arcnum);//把输入的值保存到图结构体中


    for(i = 0; i < G->vexnum; i++)
    {
        printf("请输入每个顶点的值:>");
        getchar();//清除键盘缓存区的回车键
        scanf("%c", &G->head[i].data);//把输入的值保存到顶点数组当中
        G->head[i].firstarc = NULL;
    }
    for(i = 0; i < G->arcnum; i++)//有几条边，循环几次
    {
        char m,n;//用来接收两个顶点
        int j,k;//接收顶点的下标
        printf("请依次输入每一条边，格式为:ab >");
        getchar();
        scanf("%c%c",&m,&n);
        j = get_index(G->head,m);//得到输入的m的值，在顶点数组中的下标
        k = get_index(G->head,n);//得到输入的n的值，在顶点数组中的下标
        TNode* P1 = malloc(sizeof(TNode));
        P1->index = k;
        P1->nextarc = G->head[j].firstarc;
        G->head[j].firstarc = P1;
        //因为是无向图，所以还要建立一条反向的边
        TNode* P2 = malloc(sizeof(TNode));
        P2->index = j;
        P2->nextarc = G->head[k].firstarc;
        G->head[k].firstarc = P2;
    }
}



void InitSQ(SQ* Q)//创建并初始化一个队列
{
    Q->arr = (TNode*)malloc(sizeof(TNode)*MAXSIZE);//定义一个10个整型大小空间的数组
    Q->front = Q->back = 0;//队列置空

}
void push_sq(SQ* Q, HNode e)//插入规则，从队尾插入
{
    if((Q->back+1)%MAXSIZE == Q->front)//判断队列是否满
    {
        printf("error!,队列已经满了！");
    }
    else
    {
        Q->arr[Q->back] = e;
        Q->back = (Q->back + 1)%MAXSIZE;
    }
}
void pop_sq(SQ* Q)//删除规则，从队头删除
{
    if(Q->front == Q->back)//判断队列是否空
    {
        printf("error!,队列已经空了！");
    }
    else
    {
        HNode tmp = Q->arr[Q->front];
        Q->front = (Q->front + 1)%MAXSIZE;
        return;
    }
}
int length_sq(SQ* Q)
{
    return (Q->back - Q->front + MAXSIZE)%MAXSIZE;
}