Pytorch学习笔记---4:张量大小、偏移量和步长
张量元数据:大小、偏移量和步长
为了在存储区中建立索引,张量依赖于一些明确定义它们的信息:大小、偏移量和步长。如下示图显示了它们如何相互作用。
我们可以通过提供相应的索引来得到张量中的第2个点:
①偏移量
points = torch.tensor([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]])
second_point = points[1]
print(second_point.storage_offset())
print(second_point.size())
print(second_point.shape)2
torch.Size([2])
torch.Size([2])得到的张量在存储区中的偏移量为2,这是因为我们需要跳过第一个点,该点有两个元素。需要重点注意的是:函数size()所包含的信息与张量对象的shape属性所包含的信息是一样的。
②步长
步长是一个元组,指示当索引在每个维度中增加1时在存储区中必须跳过的元素数量。例如:points的步长为(2, 1).
print(points.stride())(2, 1)访问一个二维张量中的位置(i, j)的元素会导致访问存储中的第storage_offset+stride[0]*i+stride[1]*j个元素。偏移量通常为0,如果这个张量时为容纳更大的张量而创建的存储视图,那么偏移量可以为正值。
这种张量和存储区之间的间接关系使得一些操作开销并不大,如转置一个张量或者提取一个子张量,因为它们不会导致内存重新分配,而是创建一个新的张良对象,该张量具有不同的大小、偏移量和步长。
当我们索引一个特定的点,同时看到偏移量增加时,表面我们已经提取了一个子张量,让我们看看大小和步长发生了什么变化。
points = torch.tensor([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]])
second_point = points[1]
print(second_point.size())
print(second_point.storage_offset())
print(second_point.stride())torch.Size([2])
2
(1,)重要的是,正如我们语气的那样,子张量的维度少了一维,同时仍然索引了与原始张量points相同的存储区。这也意味着更改子张量会对原始张量产生影响。
如果不希望修改子张量会改变源张量的元素,可以对子张量进行复制操作:
points = torch.tensor([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]])
second_point = points[1].clone()
second_point[0] = 10.0
print(points)
print(second_point)tensor([[4., 1.],
[5., 3.],
[2., 1.]])
tensor([10., 3.])③无复制转置
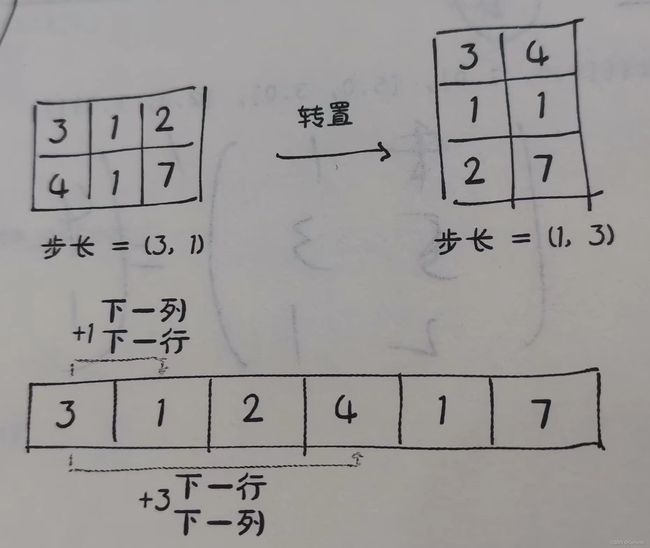
我们使用张量points,它在行中有单独的点,在列中有x和y坐标,然后将其转置,使各个点都在列中。转置由t()方法完成,它是用于二维张量转置的transpose()方法的简写。
points = torch.tensor([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]])
points_t = points.t()
print(points)
print(points_t)tensor([[4., 1.],
[5., 3.],
[2., 1.]])
tensor([[4., 5., 2.],
[1., 3., 1.]])但其实这两个张量共享同一个存储区,只不过是形状和步长上有所不同:
print(id(points.storage()) == id(points_t.storage()))
print(points.stride(), points_t.stride())True
(2, 1) (1, 2)如下所示的图很好的解释了这一切:
高维张量转置:
Pytoch中的转置不限于矩阵。我们可以通过指定两个维度,即翻转形状和步长,来转置一个多维数组。
first = torch.ones(3, 4, 5)
transpose_t = first.transpose(0, 2)
print(first.shape, first.stride())
print(transpose_t.shape, transpose_t.stride())torch.Size([3, 4, 5]) (20, 5, 1)
torch.Size([5, 4, 3]) (1, 5, 20)总结:张量的偏移量、大小和步长之间的关系