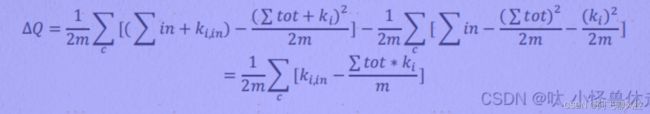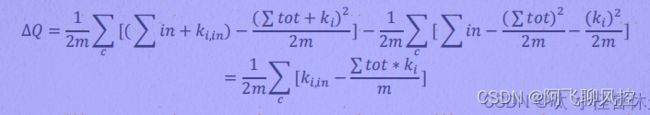社区发现系列02-算法介绍
一、社区发现算法
1.1 LPA标签传播算法
1、基本思想:
标签传播算法是不重叠社区发现的经典算法,其基本思想是:将一个节点的邻居节点的标签中数量最多的标签作为该节点自身的标签。给每个节点添加标签(label)以代表它所属的社区,并通过标签的“传播”形成同一标签的“社区”结构。
给每个节点添加标签(label)以代表它所属的社区,并通过标签的“传播”形成同一标签的“社区”结构。一个节点的标签取决于它邻居节点的标签:假设节点z的邻居节点有z1至zk,那么哪个社区包含z的邻居节点最多z就属于那个社区(或者说z的邻居中包含哪个社区的标签最多,z就属于哪个社区)。优点是收敛周期短,无需任何先验参数(不需事先指定社区个数和大小),算法执行过程中不需要计算任何社区指标。
时间复杂度接近线性:对顶点分配标签的复杂度为O(n),每次迭代时间为O( m),找出所有社区的复杂度为O (n +m),但迭代次数难以估计
2、传播过程:
1)初始时,给每个节点一个唯一的标签;
2)每个节点使用其邻居节点的标签中最多的标签来更新自身的标签。
3)反复执行步骤2),直到每个节点的标签都不再发生变化为止。
一次迭代过程中一个节点标签的更新可以分为同步和异步两种。所谓同步更新,即节点z在第t次迭代的label依据于它的邻居节点在第t-1次迭代时所得的label;异步更新,即节点z在第t次迭代的label依据于第t次迭代已经更新过label的节点和第t次迭代未更新过label的节点在第t-1次迭代时的label。
注:
1、迭代次数设定一个阈值,可以防止过度运算;
2、对于二分图等网络结构,同步更新会引起震荡;
//3、类似(“强”社区>)定义的结构(该社区>=);
4、每个顶点在初始的时候赋予唯一的标签,即“重要性”相同,而迭代过程又采用随机序列,会导致同一初始状态不同结果甚至巨型社区的出现;
5、如果能预测“社区中心”点,能有效提高社区发现的准确度,大幅提高效率;
6、同一节点的邻居节点的标签可能存在多种社区最大数目相同的情况,取“随机”一个作为其标签
3、算法改进思路:初始化或传播改进
1)给节点或边添加权重(势函数、模块密度优化、LeaderRank值、局部拓扑信息的相似度、标签从属系数等),信息熵等描述节点的传播优先度,进而初步确定社区中心点以提高社区划分的精度;
2)标签初始化改进,如提取一些较为紧密的子结构来作为标签传播的初始标签(非重叠最小极大团提取算法 orz。。。)或通过初始社区划分算法先确定社区的雏形再进行传播。
3)标签随机选择改进,将1)中的权值和节点邻接点的度数等作为参考因素,对标签更新过程进行修正。
1)在社区中寻找不重叠三角形作为起始簇的雏形,以提高算法结果的稳定性和运行效率;
2)添加标签熵属性,在迭代过程中不采用随机序列,而是根据每个节点的标签熵来排序序列;
3)在2)的基础上,为了不完全消除标签传播算法的随机性,将排序好的队列平均分成三个部分,在每个部分内,节点进行随机排列。
4)对于同一节点的邻居节点的标签可能存在多种社区最大数目相同的情况,不使用随机方法,而是分析该节点的邻节点的邻节点集标签分布情况来决定该节点的标签
5)在社区中寻找以度最大的若干节点为中心的“雪花型”结构作为起始簇的雏形
1.2 Louvain算法(基于模块度的层次型社区发现算法)
1、 算法的思想:
2、 模块度和模块度的增益
1.3、CPM算法
k-团渗透算法(CPM)[1]是第一个能够发现重叠社区的算法,重叠社区指的是结点可以同时属于多个社区。重叠社区在社交网络中是十分常见的,因为每个人都有着多种多样的社交关系。
网络中的最大团指的是,团中任意两个结点之间都有边连接,并且它不被其他的团所包含。
CPM算法的想法非常简单,首先它找出网络中所有大小至少为k的最大团。然后构建一个团图,每个最大团都是团图中的一个结点,如果两个团c1与c2共享min(c1,c2)-1个邻居的话,它们在新图中的结点之间就存在边。最后团图中的每个连通单元就是一个结点的社区,而它可能是重叠的。
代码参见:https://github.com/zzz24512653/CommunityDetection/blob/master/algorithm/CPM.py1.4、GN算法(分裂性社区发现算法)
(1)计算每一条边的边介数;
(2)删除边界数最大的边;
(3)重新计算网络中剩下的边的边阶数;
(4)重复(3)和(4)步骤,直到网络中的任一顶点作为一个社区为止。
(2)在计算边介数的时候可能会有很对重复计算最短路径的情况,时间复杂度太高;
(3)GN算法不能判断算法终止位置。
二、不同算法的社区划分效果:
1、样本:
2、社区划分软件:pajek、networkx
- networkx是python的一个第三方包,可以方便地调用各种图算法的计算。
- 将NetworkX中的网络转成Pajek可以读取的网络,实际上只需要一条语句: nx.write_pajek(G,'Pajek.net')
- 然后就可以用Pajek打开这个文件,具体而言,启动Pajek界面后,选择“Network”下的第一个图标,然后打开。这里再简单总结一下这个软件的使用。例如,对于刚才打开的网络,可以进行社团发现,操作如下:
- 在菜单栏中点Network——Create Partition——Communities——Louvain Method,选择任一种算法,运行后就可以在Partitions这一栏生成结果。
- 对于这样的社团划分结果,我们希望能把结果可视化出来,那么只需要选择Draw——Network + First Partition即可。就简单总结这么多,希望能帮助大家在熟悉NetworkX的前提下迅速掌握Pajek的使用方法。
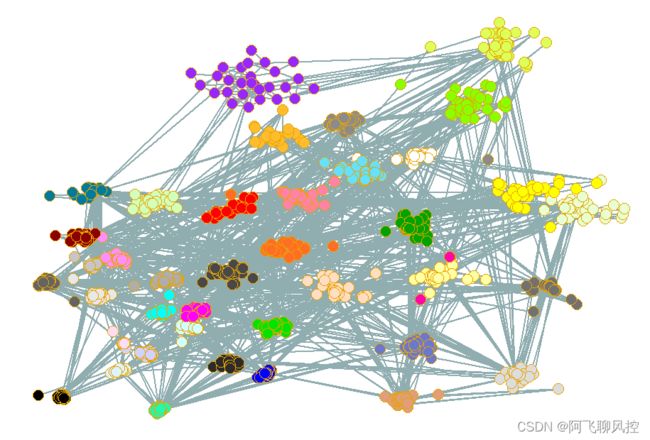
4、不同社区划分算法的实验结果
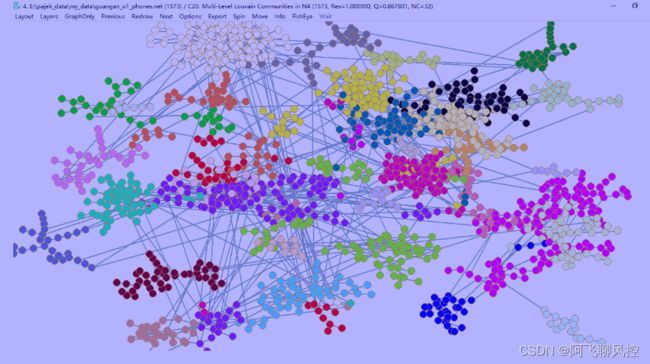
实验1 Louvain算法:
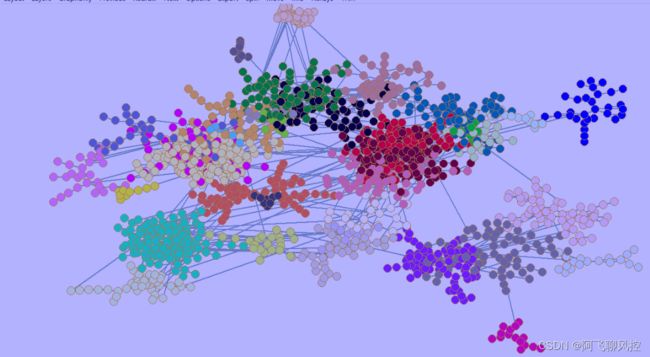
实验2:GN算法