PRML读书会第五期——概率图模型(Graphical Models)【中】

注：这是全文的第二部分，前后文传送门：
PRML读书会第五期——概率图模型(Graphical Models)【上】
PRML读书会第五期——概率图模型(Graphical Models)【下】

算法推导

符号与规定

为了保证行文中符号的一致性，在推导中采取如下的符号体系：

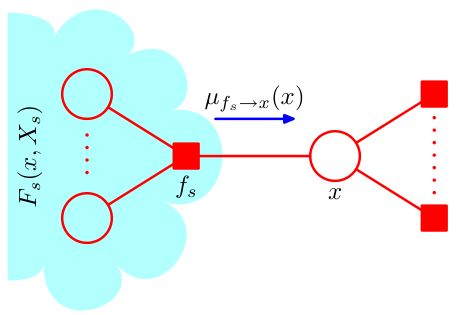
与上文一致地，$X$代表全体随机变量，$x(x_i)$代表某一随机变量。此处，我们的任务为求变量$x$的边缘概率。

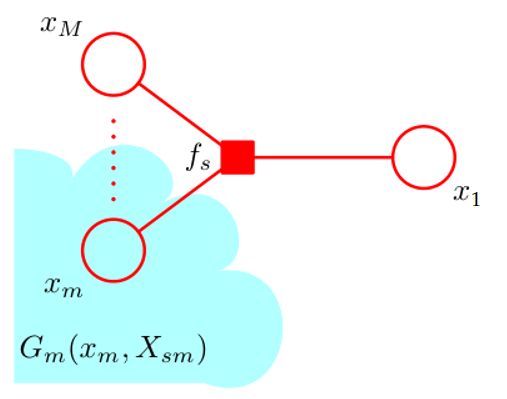
由于算法在具有树结构的因子图上进行，我们考虑每一个与$x$相连的因子，$x$通过这些因子与图的其它部分相关联。我们记这些因子节点为$f_{S_a},f_{S_b},\cdots$.一般的，我们将任一$f_{S_n}$视作$f_S$以简化讨论。于此同时，我们规定$X_{S_a},X_{S_b},\cdots$，它们是通过对应因子节点$f_{S_a},f_{S_b},\cdots$与$x$相连的子树中的所有节点对应的随机变量组成的集合，如图所示。同样的，我们将任一$X_{S_n}$视作$X_S$.

在此基础上我们定义$x$关于$f_S$的邻居$x_1,x_2,\cdots ,x_M$，因子$f_S$正是定义在$x$与它关于$f_S$的邻居们构成的集合上的。

进一步地，我们将$X_S$中通过邻居节点$x_m$与$f_S$相连的子树中的所有节点对应的随机变量组成的集合记作$X_{Sm}$，如图中的$X_{S1}$.与刚才定义$X_S$时类似，我们在$x_m$的基础上定义$f_l$与$X_{ml}$：与$x_m$直接相连的因子节点，除$f_S$外，其余因子节点分别记为$f_{l_a},f_{l_b},\cdots$，并一般化地记为$f_l$；通过$f_l$与$x_m$相连的子树中的所有节点对应的随机变量的集合记作$X_{ml}$。

于此同时，我们用$ne$来记邻居构成的集合。对于变量节点$x_i$来说，$ne(x_i)$是与$x_i$相连的所有因子节点的集合；对于因子节点$f_S$来说，$ne(f_S)$是所有与$f_S$相连的变量节点的集合。特别的，当我们说节点集合$S\in ne(x_i)$时，$S$实际上指的是上文中规定的$f_S$对应的$X_S$对应的节点集合，即$S$是由通过因子节点$f_S$与$x$相连的子树中的所有节点构成的。

除此之外，我们使用省略号来略去与通过因子节点与讨论对象相连的子树部分。我们还将在变量和变量集合的层面上定义一些函数，如$F_S$是由因子节点$f_S$关联起来的随机变量在联合概率中的因子之积，具体来说是联合概率中涉及与$f_S$对应地$X_S$与$x$的所有因子；而$G_m$是通过$x_m$对应的节点（包括$x_m$本身）从而与因子节点$f_S$关联起来的随机变量在联合概率中的因子之积，具体来说是联合概率中涉及与$x_m$对应地$X_{Sm}$及$x_m$的所有因子；而其余的函数将在具体推导中给出相应的定义。

总结一下，小写字母$x$通常代表了随机变量，大写字母$X$通常代表了变量集合，而$X_S$的下标$S$为随机变量集合在图中对应的节点集合，对于函数$G,F$，可以简单的通过它们所接受的自变量来判断它们代表了联合概率中的哪一部分因子（$F$面向因子节点进行定义，而$G$面向变量节点进行定义）。算法的具体推导过程并不是十分复杂，如果忘记了记号的具体含义，可以参照上述图示。

注：

1. 原书中仅通过图示的手段给出了部分记号的含义，容易使读者感到一头雾水；尽管将所有的记号全部给出会给读者带来一定的心理压力，但配合综合图示，在感到困惑时能够有迹可循

2. 或是迫于时间压力，主讲人仅给出了半个算法的部分推导。这里将按照书本顺序将其补全

3. 书中此处采用小写s来指代变量集合，为了与前文风格保持一致，采用了大写S，具体算式可能与书中摘录的图示稍有出入

下文为连续的推导过程，处于简洁考虑，所有式子默认采用$(\ast )$标注，式前的$(\ast )$默认指上一个式子。

推导过程

先明确我们的目标：求边缘概率$p(x)$.由加法原理，我们有
$$p(x)=\sum _{X\setminus x}p(X)$$
引入因子图中因子分解的概念，我们有
$$p(X)=\prod _S{f}_S(X_S)$$
此处对因子$S$的划分较为自由。结合具体任务，我们选定如下的划分方式
$$p(X)=\prod _{S\in ne(x)}{F}_S(x,X_S)$$
事实上，在上述对$X_S$的定义过程中已经蕴含了这种划分的背后的思想。由于算法在具有树结构的因子图上进行，$x$通过与之相连的因子节点与整张图其余部分相连；换句话说，对$\forall S\in ne(x)$，即$S$取遍$f_{S_a},f_{S_b},\cdots$时，$F_S(x,X_S)$也将取遍联合概率中的所有因子；自然而然地，$F_S$定义在$\{x\}\cup X_S$上，指代了涉及这些随机变量的因子。

将此处的$p(X)$带入边缘概率的表达式，得
$$p(x)=\sum _{X\setminus x}\prod _{S\in ne(x)}{F}_S(x,X_S)(\ast )$$
既然$S$能将$x$外的节点取遍，我们自然可以利用$S$来拆解求和号
$$(\ast )=\sum _{X_{S_a}}\sum _{X_{S_b}}\cdots \sum _{X_{S_n}}\prod _{S\in ne(x)}{F}_S(x,X_S)(\ast )$$
将累乘写开，利用乘法分配律作进一步的化简
$$\begin{gathered} (\ast )=\sum _{X_{S_a}}\sum _{X_{S_b}}\cdots \sum _{X_{S_n}}{F}_{S_a}(x,X_{S_a})F_{S_b}(x,X_{S_b})\cdots F_{S_n}(x,X_{S_n}) \\ =\sum _{X_{S_a}}{F}_{S_a}(x,X_{S_a})\sum _{X_{S_b}}{F}_{S_b}(x,X_{S_b})\cdots \sum _{X_{S_n}}{F}_{S_n}(x,X_{S_n}) \\ =[\sum _{X_{S_a}}{F}_{S_a}(x,X_{S_a})][\sum _{X_{S_b}}{F}_{S_b}(x,X_{S_b})]\cdots [\sum _{X_{S_n}}{F}_{S_n}(x,X_{S_n})] \\ =\prod _{S\in ne(x)}\sum _{X_S}{F}_S(x,X_S) \end{gathered}$$
其中最后一步利用累乘符号对结果进行简化。

我们已经得到了一个相对简单的结果，我们作定义
$${\mu }_{f_S\to x}(x)\triangleq \sum _{X_S}{F}_S(x,X_S)$$
从上述过程中我们可以看出，若应用将乘法分配律的步骤称为变量消除法，那么每一个因式中，${\mu }_{f_S\to x}(x)$携带了整个式子中与$f_S$有关的全部“信息"，通过累乘的方式将它们传递到我们的目标中，如图：

这便是从因子节点到变量节点的”信念传播“。

由于$F_S$还可以继续化简，我们将$F_S$中的因子展开出来，有
$$F_S(x,X_S)=f_S(x_1,x_2,\dots ,x_M)G_1(x_1,X_{S1})G_2(x_2,X_{S2})\cdots G_M(x_M,X_{SM})$$
从定义的图示中我们能很明显看出它的正确性：$F_S(x,X_S)$囊括了$\{x\}\cup X_S$对应的节点，这些节点包括了$f_S$本身涵盖的节点（即$x$与$x$关于$f_S$的邻居节点），还有与这些邻居节点相连的子树部分。由于条件独立性的存在，在$\{x\}\cup X_S$中，$x$仅与这些邻居节点有关，而与其余的子树无关，故可将这些子树部分的因子写作对应$G_m(x_m,X_{SM})$的乘积。

将上述分解形式带入${\mu }_{f_S\to x}(x)$得
$${\mu }_{f_S\to x}(x)=\sum _{X_S}{f}_S(x_1,x_2,\dots ,x_M)G_1(x_1,X_{S1})G_2(x_2,X_{S2})\cdots G_M(x_M,X_{SM})(\ast )$$
根据上述讨论，对$X_S$进行拆分
$$X_S=\{x_1\}\cup \{x_2\}\cup \cdots \cup \{x_M\}\cup X_{S1}\cup X_{S2}\cup \cdots \cup X_{SM}$$
在此基础上利用分配律对原式进行化简
$$\begin{gathered} (\ast )=\sum _{x_1}\cdots \sum _{x_M}\sum _{X_{S1}}\cdots \sum _{X_{SM}}{f}_S(x_1,x_2,\dots ,x_M)G_1(x_1,X_{S1})G_2(x_2,X_{S2})\cdots G_M(x_M,X_{SM}) \\ =\sum _{x_1}\cdots \sum _{x_M}{f}_S(x_1,x_2,\dots ,x_M)\sum _{X_{S1}}{G}_1(x_1,X_{S1})\cdots \sum _{X_{SM}}{G}_M(x_M,X_{SM}) \\ =\sum _{x_1}\cdots \sum _{x_M}{f}_S(x_1,x_2,\dots ,x_M)[\sum _{X_{S1}}{G}_1(x_1,X_{S1})]\cdots [\sum _{X_{SM}}{G}_M(x_M,X_{SM})] \\ =\sum _{x_1}\cdots \sum _{x_M}{f}_S(x_1,x_2,\dots ,x_M)\prod _{m\in ne(f_S)\setminus \{x\}}\sum _{X_{Sm}}{G}_m(x_m,X_{Sm}) \end{gathered}$$
其中最后一步用$ne(f_S)\setminus \{x\}$对这些$x$关于$f_S$的邻居进行刻画，从而写作累乘形式以化简。注意，因子$G_m(x_m,X_{Sm})$依赖于$x_m$，需要$\sum _{x_m}$提供的求和环境，故不可以提到前面去。

仿照前面定义${\mu }_{f_S\to x}(x)$的做法，我们作定义
$${\mu }_{x_m\to f_S}(x_m)\triangleq \sum _{X_{Sm}}{G}_m(x_m,X_{Sm})$$
同样的，我们可以认为${\mu }_{x_m\to f_S}(x_m)$携带了与之关联的子树$X_{S_m}$中的全部信息，如图：

这便是变量节点到因子节点的“信念传播”。结合上述因子节点到变量节点的“信念传播”，从图中我们可以直观的理解这一连续的过程。

继续化简$G_m(x_m,X_{Sm})$，不难发现，以$x_m$为根的子树的结构，与将$x$作为原树根节点的树结构完全一致。仿照前面的划分，我们有
$$G_m(x_m,X_{Sm})=\prod _{l\in ne(x_m)\setminus f_S}{F}_l(x_m,X_{ml})$$
由于在子树中复现前文的操作，我们需要将$f_S$节点从$ne(x_m)$中剔除。

同样的，将上述分解形式带入${\mu }_{x_m\to f_S}(x_m)$得
$${\mu }_{x_m\to f_S}(x_m)=\sum _{X_{Sm}}\prod _{l\in ne(x_m)\setminus f_S}{F}_l(x_m,X_{ml})(\ast )$$
同样的，我们利用$l$来拆分求和号，并将累乘写开
$$\begin{gathered} (\ast )=\sum _{X_{l_a}}\sum _{X_{l_b}}\cdots \sum _{X_{l_n}}\prod _{l\in ne(x_m)\setminus f_S}{F}_l(x_m,X_{ml}) \\ =\sum _{X_{l_a}}\sum _{X_{l_b}}\cdots \sum _{X_{l_n}}{F}_{l_a}(x_m,X_{m{l}_a})F_{l_b}(x_m,X_{m{l}_b})\cdots F_{l_n}(x_m,X_{m{l}_n}) \\ =\sum _{X_{l_a}}{F}_{l_a}(x_m,X_{m{l}_a})\sum _{X_{l_b}}{F}_{l_b}(x_m,X_{m{l}_b})\cdots \sum _{X_{l_n}}{F}_{l_n}(x_m,X_{m{l}_n}) \\ =[\sum _{X_{l_a}}{F}_{l_a}(x_m,X_{m{l}_a})][\sum _{X_{l_b}}{F}_{l_b}(x_m,X_{m{l}_b})]\cdots [\sum _{X_{l_n}}{F}_{l_n}(x_m,X_{m{l}_n})] \\ =\prod _{l\in ne(x_m)\setminus f_S}\sum _{X_l}{F}_l(x_m,X_{ml})=\prod _{l\in ne(x_m)\setminus f_S}{\mu }_{f_l\to x_m}(x_m) \end{gathered}$$
最后同样利用累乘将其合并，而累乘的对象正是上文定义的因子节点到变量节点“信念传播”的形式。上述推导过程如图所示：

至此，Sum-Product算法的主体推导完成。下面对边界进行讨论：

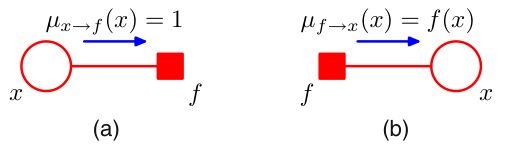
直接带入上述推导结果，不难得出，对于叶型随机变量节点，${\mu }_{x\to f}(x)=1$，而对于叶型因子节点，${\mu }_{f\to x}(x)=f(x)$.

Sum-Product算法总结如下：
$$\{\begin{array}{l}p(x)=\prod _{S\in ne(x)}{\mu }_{f_S\to x}(x)\\ {\mu }_{f\to x}(x)=\sum _{x_1,\cdots ,x_M}f(x,x_1,\cdots ,x_M)\prod _{m\in ne(f)\setminus x}{\mu }_{x_m\to f}(x_m)\\ {\mu }_{x\to f}(x)=\prod _{l\in ne(x)\setminus f}{\mu }_{f_l\to x}(x)\end{array}$$
在推导过程中，我们并没有考虑到归一化的问题。事实上，我们可以通过对其中任意一个随机变量进行归一化，从而得到整体共用的归一化常数。

实例

下用实例来验证Sum-Product算法的正确性。

在利用算法进行具体操作时，我们随机选定根节点，既可以时变量节点，又可以是因子节点。从根节点出发，我们先递后归求出所有${\mu }_{f_S\to x}$与${\mu }_{x_m\to f_S}$；利用上面总结中的第一条，我们可以利用这些“信息”表达出所有的边缘概率。

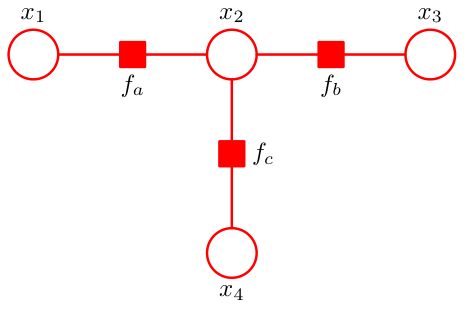
如图，根据因子图的形式，我们写出它联合概率的因子分解
$$\tilde{p}(X)=f_a(x_1,x_2)f_b(x_2,x_3)f_c(x_2,x_4)$$
这里，我们使用$\tilde{p}$来指代未归一化的概率。

我们的目的是求解$\tilde{p}(x_2)$.

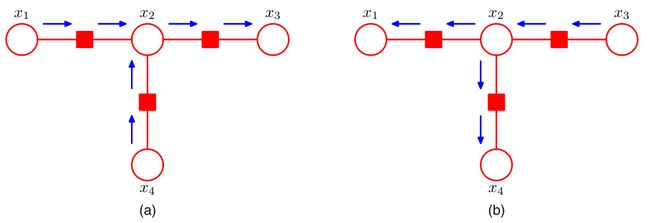
现选定$x_3$作根节点，分别从叶子向根、从根向叶子写出全部的信息：

图(a)：叶子$\to$根
$$\begin{gathered} {\mu }_{x_1\to f_a}(x_1)=1 \\ {\mu }_{f_a\to x_2}(x_2)=\sum _{x_1}{f}_a(x_1,x_2) \\ {\mu }_{x_4\to f_c}(x_4)=1 \\ {\mu }_{f_c\to x_2}(x_2)=\sum _{x_4}{f}_c(x_2,x_4) \\ {\mu }_{x_2\to f_b}(x_2)={\mu }_{f_a\to x_2}(x_2){\mu }_{f_c\to x_2}(x_2) \\ {\mu }_{f_b\to x_3}(x_3)=\sum _{x_2}{f}_b(x_2,x_3){\mu }_{x_2\to f_b}(x_2) \end{gathered}$$

图(b)：根$\to$叶子
$$\begin{gathered} {\mu }_{x_3\to f_b}(x_3)=1 \\ {\mu }_{f_b\to x_2}(x_2)=\sum _{x_3}{f}_b(x_2,x_3) \\ {\mu }_{x_2\to f_a}(x_2)={\mu }_{f_b\to x_2}(x_2){\mu }_{f_c\to x_2}(x_2) \\ {\mu }_{f_a\to x_1}(x_1)=\sum _{x_2}{f}_a(x_1,x_2){\mu }_{x_2\to f_a}(x_2) \\ {\mu }_{x_2\to f_c}(x_2)={\mu }_{f_a\to x_2}(x_2){\mu }_{f_b\to x_2}(x_2) \\ {\mu }_{f_c\to x_4}(x_4)=\sum _{x_2}{f}_c(x_2,x_4){\mu }_{x_2\to f_c}(x_2) \end{gathered}$$

注：按叶子到根的顺序能够保证其中的每个节点在向下继续传递信息前，能够收集到足够的信息；而从根到叶子的传递过程中，根成了唯一的信息源，故需要利用先前叶子传递到根的信息，所里两个步骤具有先后顺序

在此基础上，我们得到
$$\begin{gathered} \tilde{p}(x_2)={\mu }_{f_a\to x_2}(x_2){\mu }_{f_b\to x_2}(x_2){\mu }_{f_c\to x_2}(x_2) \\ =\sum _{x_1}{f}_a(x_1,x_2)\sum _{x_3}{f}_b(x_2,x_3)\sum _{x_4}{f}_c(x_2,x_4) \end{gathered}$$
而纯粹利用变量消除法，我们有
$$\begin{gathered} \tilde{p}(x_2)=\sum _{x_1,x_3,x_4}p(X) \\ =\sum _{x_1}\sum _{x_3}\sum _{x_4}{f}_a(x_1,x_2)f_b(x_2,x_3)f_c(x_2,x_4) \\ =\sum _{x_1}{f}_a(x_1,x_2)\sum _{x_3}{f}_b(x_2,x_3)\sum _{x_4}{f}_c(x_2,x_4) \end{gathered}$$
二者结果一致，即验证了Sum-Product算法的正确性。

衍生算法

回到我们的推断任务上来，我们需要解决边缘概率、条件概率与最大后验三个问题。利用上述的Sum-Product算法，我们已经能够高效地完成第一个任务——求边缘概率。

而对于求解条件概率，利用贝叶斯法则，我们有
$$p(X_A|X_B)=\frac{p(X_A,X_B)}{p(X_B)}$$
我们不再是求单个变量的边缘概率，而是求解变量集合的边缘概率。

求解随机变量集合的边缘概率

如图，与上文处理$F_S(x,X_S)$时采取的手法一致地，我们将联合概率拆解为
$$p(X)=f_S(X_S)\prod _{m\in ne(f_S)}{G}_m(x_m,X_{Sm})$$

这里的$X_S$与上文中的含义略有不同，此处指$f_S$关联起来的目标变量集合

利用加法法则，我们有
$$\begin{gathered} p(X_S)=\sum _{X\setminus X_S}p(X) \\ =\sum _{X\setminus X_S}{f}_S(X_S)\prod _{m\in ne(f_S)}{G}_m(x_m,X_{Sm}) \\ =f_S(X_S)\sum _{X\setminus X_S}\prod _{m\in ne(f_S)}{G}_m(x_m,X_{Sm})(\ast ) \end{gathered}$$
同样的，我们对$X\setminus X_S$有如下拆分
$$X\setminus X_S=X_{S1}\cup X_{S2}\cup \cdots \cup X_{SM}=\bigcup _{i\in ne(f_S)}{X}_{Si}$$
利用上述结果将求和号打开
$$\begin{gathered} (\ast )=f_S(X_S)\sum _{X_{S1}}\cdots \sum _{X_{SM}}{G}_1(x_1,X_{S1})\cdots G_M(x_M,X_{SM}) \\ =f_S(X_S)\sum _{X_{S1}}{G}_1(x_1,X_{S1})\cdots \sum _{X_{SM}}{G}_M(x_M,X_{SM}) \\ =f_S(X_S)[\sum _{X_{S1}}{G}_1(x_1,X_{S1})]\cdots [\sum _{X_{SM}}{G}_M(x_M,X_{SM})] \\ =f_S(X_S)\prod _{i\in ne(f_S)}\sum _{X_{Si}}{G}_i(x_i,X_{Si}) \end{gathered}$$
最后，根据${\mu }_{x\to f}(x)$的定义，我们最终得到
$$p(X_S)=f_S(X_S)\prod _{i\in ne(f_S)}{\mu }_{x_i\to f_S}(x_i)$$
这样，我们可以利用Sum-Product得到的信息求得随机变量集合的边缘概率。

观测变量处理

上述讨论中，我们默认所有变量都是未观测变量，而对于观测变量来说，只需对联合概率作小小的改进即可胜任。

假设$X=h\cup v$，其中$h$为隐变量，$v$为观测变量，且观测值为$\hat{v}$.我们向联合概率中引入一些因子，得到
$$p(h,v=\hat{v})=p(X)\prod _{i}I(v_i,\widehat{v_i})$$
其中，
$$I(v,\hat{v})=\{\begin{array}{ll}1,& v=\hat{v},\\ 0,& v\ne \hat{v}.\end{array}$$

求最大后验

即要求$X^{max}=\underset{X}{\mathrm{argmax}}p(X)$.

我们先考虑一个稍微弱化的任务：不求出联合概率最大时变量的具体取值，而是求出对应的最大概率，即
$$p(X^{max})=\underset{X}{\max }p(X)$$
事实上，$max$与$\sum$一样，是可以拆解的。我们想求三个数的最大值，可以先求出其中两个数的最大值，再与第三数进行比较。

因此，我们有
$$\underset{X}{\max }p(X)=\underset{x_1}{\max }\underset{x_2}{\max }\cdots \underset{x_3}{\max }p(X)$$
同样的，乘法关于最大值的分配律依然成立，即$c\cdot \max (a,b)=\max (ca,cb)$.既然如此，我们依旧可以用理解$\sum$的方式来理解$\max$.而针对最大后验值，从形式上来说，与求解某一变量的边缘概率几乎一致，只不过求边缘概率时不需要对所求的目标变量求和，故求最大后验时会多一层$\max$。

将Sum-Product算法的$\sum$改写为$\max$，就得到了所谓的Max-Product算法，即
$$\{\begin{array}{l}\underset{X}{\max }p(X)=\underset{x}{\max }\prod _{S\in ne(x)}{\mu }_{f_S\to x}(x)\\ {\mu }_{f\to x}(x)=\underset{x_1,\cdots ,x_M}{\max }f(x,x_1,\cdots ,x_M)\prod _{m\in ne(f)\setminus x}{\mu }_{x_m\to f}(x_m)\\ {\mu }_{x\to f}(x)=\prod _{l\in ne(x)\setminus f}{\mu }_{f_l\to x}(x)\end{array}$$
同样的，我们选定一个根节点，并且只需要将信息从叶子传递到根即可；最后，针对$x$的不同取值求出其最大值，即为最大后验的值。

整个求解过程是一个动态规划(Dynamic Programming)，我们通过不断的对部分随机变量进行优化，最终得到全局的最优解。

同样的，我们可以利用动态规划中的常见的反向追踪(back-tracking)手法来求得$X^{max}$.在每次进行从当前最优化的$x_{n-1}^{max}$到$x_n$状态转移时，我们都记录下它的来源，记
$$\varphi (x_n)=x_{n-1}^{\max }$$
这样，在我们求得最后根节点$x^{max}$后，将它带到$\varphi$中，就可以找出$X^{max}$的具体取值了，如下图：

但Max-Product算法还有优化的空间。不难看出，我们对这些因子进行了多次乘法，而这些因子是联合概率的组成部分。实际应用中，对一个小于1的浮点数进行多次乘法，对精度构成了挑战，而简单的取一个对数便能将乘法化为加法，完美的解决问题，如下
$$\{\begin{array}{l}\ln \underset{X}{\max }p(X)=\underset{x}{\max }[\sum _{S\in ne(x)}{\mu }_{f_S\to x}(x)]\\ {\mu }_{f\to x}(x)=\underset{x_1,\cdots ,x_M}{\max }[\ln f(x,x_1,\cdots ,x_M)+\sum _{m\in ne(f)\setminus x}{\mu }_{x_m\to f}(x_m)]\\ {\mu }_{x\to f}(x)=\sum _{l\in ne(x)\setminus f}{\mu }_{f_l\to x}(x)\end{array}$$
具体地，我们取$\varphi (x_n)$为
$$\varphi (x_n)=\underset{x_{n-1}}{\mathrm{argmax}}[\ln f_{n-1,n}(x_{n-1},x_n)+{\mu }_{x_{n-1}\to f_{n-1,n}}(x_n)]$$
相应地，边界条件也发生了改变
$${\mu }_{x\to f}(x)=0,{\mu }_{f\to x}(x)=\ln f(x)$$
Max-Product(Max-Sum)算法可以看作是对Viterbi算法的推广。

后续内容书中点到为止，此处亦不做具体展开。

下文传送门：
PRML读书会第五期——概率图模型(Graphical Models)【下】