非均匀三次B样条曲线插值实现及MATLAB代码
这篇博客跟我上一篇博客《均匀三次B样条曲线插值实现及MATLAB代码》的内容有点像，只是在基函数的计算上不同，造成均匀/非均匀的区别。
参考资料：
[1]（这个PPT讲得很通俗，但对于多插值点分段曲线的内容漏讲了一个知识点）三次周期B样条曲线的算法 - 百度文库 (baidu.com)
[2]（这个介绍只有两个插值点的三次B样条曲线，是B样条曲线最简单的形式了吧~）(7条消息) 从B样条的插值点反求控制点_cofd的专栏-CSDN博客
[3]（一本书，里面有讲到整体参数和局部参数设置、节点矢量划分等）《计算机辅助几何设计与非均匀有理B样条》
正文：
曲线插值一般指的是给定插值点，得出曲线的方程，曲线会经过所有的插值点。确定三次B样条曲线的输入量有两种，一种是给出控制点和其它边界条件，曲线一般不经过控制点；一种是给出插值点和其它边界条件，曲线会经过所有插值点，显然第二种输入量使用更为广泛，这里只介绍第二种情况。
①首先输入插值点，这些插值点可以是二维(x,y)点，也可以是三维(x,y,z)点，甚至更多维都可以，处理方法都相似，以二维点为例，MATLAB代码：
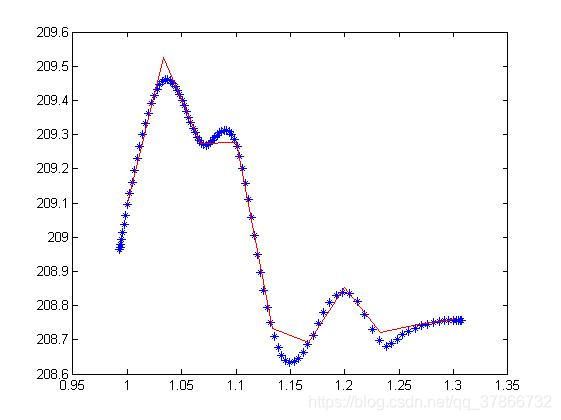
pointInput=[1 209.1;1.033 209.525;1.067 209.273;1.1 209.277;
1.133 208.734;1.167 208.693;1.2 208.852;1.233 208.722;1.267 208.746;1.3 208.759];这些点的分布如下图的红色拆线所示（不是蓝色的*型点，蓝色的是我最终拟合的曲线）。
②计算N、n、k等值
N为插值点的个数，上面共有10个插值点，所以N=10。控制点个数为N+2个。n=N+1。k为次数，这里是三次B样条曲线，所以k=3。MATLAB代码：
N=length(pointInput);
k=3;
n=N-1;③反算控制点
这里主要参考了资料[1]PPT中的内容，具体的请查看该PPT。三次B样条曲线的表达式（1）为
其中
是第i段曲线的表达式，![t(t\epsilon [0,1])](http://img.e-com-net.com/image/info8/03a6b3440d3749e3b947aca71918a68a.gif){kind=small}
是局部参数，
是第i个控制点。注意节点、节点矢量、整体参数、局部参数的区别（具体的要看资料[3]或其它相关的资料了，说明这些可能需要长篇大论哦~）。
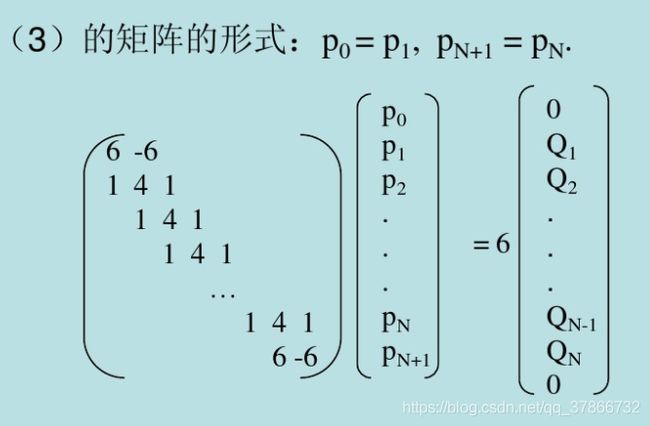
反算控制点，我用了第三种边界条件，如下图
增加了边界条件后，就能求如下图的矩阵方程了，其实下面的矩阵方程是由表达式（1）得到的，具体可以参考资料[1]的PPT（注意表达式中的系数6不要看漏了）。
对于二维点，我想对x和y坐标的B样条曲线都求出来，所以用了两组矩阵方程求解它们各自的控制点（对于三维点，还能用同样的方法求z坐标的B样条曲线）。MATLAB代码：
%①先求x、y坐标，如果是三维点，还要求z
b1=[0;pointInput(:,1);0]*6;%注意系数
px=Chase_method(A1,b1);%用追赶法求得所有控制点
b2=[0;pointInput(:,2);0]*6;
py=Chase_method(A1,b2);其中求三对角阵解用追赶法Chase_method（可以直接用常用
的方法求解，但此处用追赶法时间复杂度更低），其MATLAB代码：
function [ x ] = Chase_method( A, b )
%Chase method 追赶法求三对角矩阵的解
% A为三对角矩阵的系数，b为等式右端的常数项，返回值x即为最终的解
% 注：A尽量为方阵，b一定要为列向量
%% 求追赶法所需L及U
T = A;
for i = 2 : size(T,1)
T(i,i-1) = T(i,i-1)/T(i-1,i-1);
T(i,i) = T(i,i) - T(i-1,i) * T(i,i-1);
end
L = zeros(size(T));
L(logical(eye(size(T)))) = 1; %对角线赋值1
for i = 2:size(T,1)
for j = i-1:size(T,1)
L(i,j) = T(i,j);
break;
end
end
U = zeros(size(T));
U(logical(eye(size(T)))) = T(logical(eye(size(T))));
for i = 1:size(T,1)
for j = i+1:size(T,1)
U(i,j) = T(i,j);
break;
end
end
%% 利用matlab解矩阵方程的遍历直接求解
y = L\b;
x = U\y;
end④确定节点矢量
节点矢量是分段B样条曲线进行分段的依据（请看下资料[3]或其它相应资料），我用哈德利-贾德方法确定节点矢量![U=[u_{0},u_{1}...u_{n+k+1}]](http://img.e-com-net.com/image/info8/273b6bfadcce4859affc76a4e93760cf.gif){kind=small}
（节点矢量共有n+k+2个，注意这里是小写n而不是大写的N），即节点矢量中前k+1个节点取值0，后k+1个节点取值为1，重复度为k+1，然后中间的节点
由哈德利-贾德方法计算得到。MATLAB代码（注意MATLAB的数组和矩阵的下标是从1开始的，与公式中的从0开始有区别）：
%确定节点矢量
u=zeros(1,N+1+k+2);%0:1/(N+1+k+2-1):1;
for i=1:k+1
u(length(u)-i+1)=1;
end
l=zeros(1,N+1);%控制多边形各边长
for i=1:N+1
%注意如果用到三维点，这里要作修改
l(i)=sqrt((px(i+1)-px(i))^2+(py(i+1)-py(i))^2);
end
sum1=0;%用哈德利-贾德方法决定节点矢量
for g=k+1:N+1+1
for j=g-k:g-1
sum1=sum1+l(j);
end
end
for i=k+2:N+2
u(i)=sum(l(i-k:i-1))/sum1+u(i-1);
end计算得到了所有的控制点以及节点矢量，已经能知道该分段B样条曲线的表达式了，下面就输入一个点来测试。其实该分段B样条曲线用参数方程表示，x、y坐标都以参数u来表示，同时以节点矢量中每个节点作为分段曲线分段的边界，U中的元素的单调不减小的，后一个元素一不小于一个元素。下面MATLAB代码使u取值为测试点uTest，然后先找到uTest属于哪个分段，计算得到uTest属于score分段：
uTest=0.5;
score=find(uTest>=u,1,'last');%确定该参数方程的参数值所属的分段
if uTest==1 score=find(u==1,1)-1;end
score=score-k;%表示第score段样条曲线在用表达式(1)求出参数uTest对应的x、y坐标值之间，需要将整体变量uTest转换为局部变量t。注意uTest在整体样条曲线中的取值范围是[0,1]，而t在第score分段曲线中的取值范围是[0,1]。转换公式为
（
为节点矢量中第i+1个元素，且满足
，这里的i可由score确定），从而
，得到表达式(1)中的矩阵![[t^{3} t^{2} t^{1} 1]](http://img.e-com-net.com/image/info8/45b63a5bbb234e8daeae6a92a8b5e80d.gif){kind=small}
，MATLAB代码：
uNode=1;%上面的uTest是整体参数，用来确定是哪段曲线，要将整体参数转化为局部参数t
t=(uTest-u(score+k))/(u(score+1+k)-u(score+k));
for i=1:k
uNode=[t^i uNode];
end对比我另一篇博客《均匀三次B样条曲线插值实现及MATLAB代码》，本篇博客的样条曲线是非均匀的，即用的基函数并不是固定的值，而是由德布尔-考克斯递推公式计算得到。先求出基函数，MATLAB代码：
Nb=zeros(k+3,k+1);
for j=1:k+1
for i=1:n+1
if j==1
if i==score+k
Nb(i,j)=1; continue;
else
Nb(i,j)=0; continue;
end
else
%if u(i+j-1)-u(i)==0||u(i+j+1-1)-u(i+1)==0 continue;end
if u(i+j-1)-u(i)==0&&u(i+j+1-1)-u(i+1)==0
Nb(i,j)=0;
elseif u(i+j-1)-u(i)==0
Nb(i,j)=(u(i+j+1-1)-uTest)/(u(i+j+1-1)-u(i+1))*Nb(i+1,j-1);
elseif u(i+j+1-1)-u(i+1)==0
Nb(i,j)=(uTest-u(i))/(u(i+j-1)-u(i))*Nb(i,j-1);
else
Nb(i,j)=(uTest-u(i))/(u(i+j-1)-u(i))*Nb(i,j-1)+(u(i+j+1-1)-uTest)/(u(i+j+1-1)-u(i+1))*Nb(i+1,j-1);
end
%Nb(i,j)=(uTest-u(i))/(u(i+j-1)-u(i))*Nb(i,j-1)+(u(i+j+1-1)-uTest)/(u(i+j+1-1)-u(i+1))*Nb(i+1,j-1);
end
end
end最后由基函数和控制点计算得到梦寐以求的x、y坐标值，MATLAB代码：
Qx=0;Qy=0;
for i=score:score+k %注意非零基函数的个数
Qx=Qx+px(i)*Nb(i,k+1);
Qy=Qy+py(i)*Nb(i,k+1);
end附上全部MATLAB程序：
%三次B样条插值，给定插值点及两个边界条件，反算出控制点，由控制点得到分段曲线
%三维点(x,y,z)和二维点(x,y)的插值算法类似，控制多边形各边长l要作修改
%pointInput插值点
pointInput=[1 209.1;1.033 209.525;1.067 209.273;1.1 209.277;
1.133 208.734;1.167 208.693;1.2 208.852;1.233 208.722;1.267 208.746;1.3 208.759];
%pointInput=[0 10;5 8.66;10 0];
%用第三种边界条件 https://wenku.baidu.com/view/2482396e011ca300a6c390b3.html
N=length(pointInput);
k=3;
A1=eye(N+2,N+2)*4;
A1(1,1)=6;A1(1,2)=-6;A1(N+2,N+1)=6;A1(N+2,N+2)=-6;
for i=2:N+1
A1(i,i-1)=1;A1(i,i+1)=1;
end
%①先求x、y坐标，如果是三维点，还要求z
b1=[0;pointInput(:,1);0]*6;%注意系数
px=Chase_method(A1,b1);%用追赶法求得所有控制点
b2=[0;pointInput(:,2);0]*6;
py=Chase_method(A1,b2);
%确定节点矢量
u=zeros(1,N+1+k+2);%0:1/(N+1+k+2-1):1;
for i=1:k+1
u(length(u)-i+1)=1;
end
l=zeros(1,N+1);%控制多边形各边长
for i=1:N+1
%注意如果用到三维点，这里要作修改
l(i)=sqrt((px(i+1)-px(i))^2+(py(i+1)-py(i))^2);
end
sum1=0;%用哈德利-贾德方法决定节点矢量
for g=k+1:N+1+1
for j=g-k:g-1
sum1=sum1+l(j);
end
end
for i=k+2:N+2
u(i)=sum(l(i-k:i-1))/sum1+u(i-1);
end
%用基函数求值
%uTestArray=0:0.01:1;
for uTest=0:0.01:1
%uTest=0.5;
%u3Array=[uTest^3 uTest^2 uTest 1];%三次B样条专属
score=find(uTest>=u,1,'last');%确定该参数方程的参数值所属的分段
if uTest==1 score=find(u==1,1)-1;end
score=score-k;%表示第score段样条曲线
%用德布尔-考克斯递推公式计算基函数
Nb=zeros(k+3,k+1);
for j=1:k+1
for i=1:n+1
if j==1
if i==score+k
Nb(i,j)=1; continue;
else
Nb(i,j)=0; continue;
end
else
%if u(i+j-1)-u(i)==0||u(i+j+1-1)-u(i+1)==0 continue;end
if u(i+j-1)-u(i)==0&&u(i+j+1-1)-u(i+1)==0
Nb(i,j)=0;
elseif u(i+j-1)-u(i)==0
Nb(i,j)=(u(i+j+1-1)-uTest)/(u(i+j+1-1)-u(i+1))*Nb(i+1,j-1);
elseif u(i+j+1-1)-u(i+1)==0
Nb(i,j)=(uTest-u(i))/(u(i+j-1)-u(i))*Nb(i,j-1);
else
Nb(i,j)=(uTest-u(i))/(u(i+j-1)-u(i))*Nb(i,j-1)+(u(i+j+1-1)-uTest)/(u(i+j+1-1)-u(i+1))*Nb(i+1,j-1);
end
%Nb(i,j)=(uTest-u(i))/(u(i+j-1)-u(i))*Nb(i,j-1)+(u(i+j+1-1)-uTest)/(u(i+j+1-1)-u(i+1))*Nb(i+1,j-1);
end
end
end
Qx=0;Qy=0;
for i=score:score+k %注意非零基函数的个数
Qx=Qx+px(i)*Nb(i,k+1);
Qy=Qy+py(i)*Nb(i,k+1);
end
plot(Qx,Qy,'*');hold on;
end
plot(pointInput(:,1),pointInput(:,2),'r');function [ x ] = Chase_method( A, b )
%Chase method 追赶法求三对角矩阵的解
% A为三对角矩阵的系数，b为等式右端的常数项，返回值x即为最终的解
% 注：A尽量为方阵，b一定要为列向量
%% 求追赶法所需L及U
T = A;
for i = 2 : size(T,1)
T(i,i-1) = T(i,i-1)/T(i-1,i-1);
T(i,i) = T(i,i) - T(i-1,i) * T(i,i-1);
end
L = zeros(size(T));
L(logical(eye(size(T)))) = 1; %对角线赋值1
for i = 2:size(T,1)
for j = i-1:size(T,1)
L(i,j) = T(i,j);
break;
end
end
U = zeros(size(T));
U(logical(eye(size(T)))) = T(logical(eye(size(T))));
for i = 1:size(T,1)
for j = i+1:size(T,1)
U(i,j) = T(i,j);
break;
end
end
%% 利用matlab解矩阵方程的遍历直接求解
y = L\b;
x = U\y;
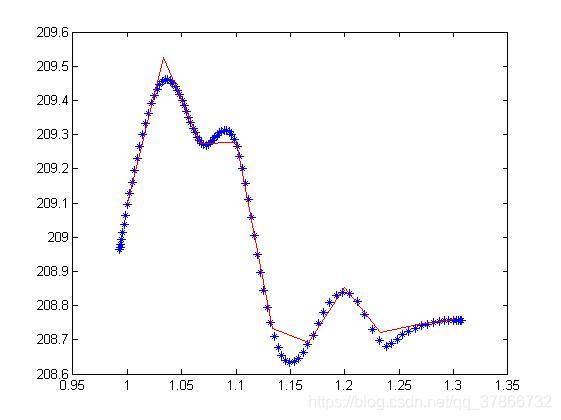
end效果图，蓝色点的是曲线拟合的点，红色拆线是由插值点组成的：
