【LSTM回归预测】基于matlab布谷鸟算法优化LSTM回归预测【含Matlab源码 2037期】
一、布谷鸟算法优化LSTM预测
1 布谷鸟搜索算法
布谷鸟算法是一种新型的群智能搜索算法,布谷鸟算法具有参数数目少、鲁棒性强、通用性好和全局寻优能力突出等多方面综合优势。布谷鸟算法以寻得全局最优鸟窝为目标,采用如式(3)所示的方法进行鸟窝位置更新:

从位置更新式(3)可以发现,布谷鸟鸟窝位置更新受到搜索步长α影响,如对搜索步长α进行有效扰动,可以对CS的前后期搜索能力进行强化和调整。本文采用引入步长扰动因子的方式进行步长扰动,步长扰动因子公式如式(4)所示,步长扰动因子可以对步长进行动态扰动,使算法搜索前期的步长较大,从而扩大搜索范围,避免陷入局部最优。后期步长较小,则可增加算法的局部探索能力,更精准的获得最优值。

式中:m表示步长扰动因子,T为设置的最大迭代次数,t为当前迭代次数。增加步长扰动后的CS的鸟窝路径及位置更新式(3)此时为:

2 LSTM
LSTM在RNN的框架基础通过增加遗忘、输入和输出3个门限,很好的解决了RNN的长期依赖问题,避免了梯度消失或梯度爆炸。LSTM的结构如图1所示。
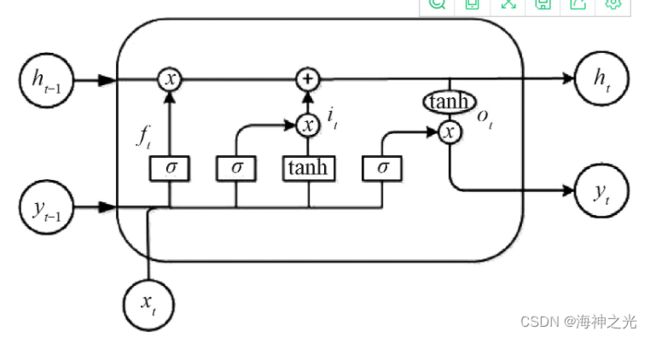
图1 LSTM模块内部结构
LSTM的各门的计算过程如下:

式(6)~(10)中,W表示各类输入循环权重,b表示偏置项;it为遗忘门,ft为输入门,ot为输出门,ct为记忆单元的向量值,σ表示范围在(0,1)之间的sigmoid函数。
LSTM 的回归拟合能力受到其网络中关键参数(如时间窗宽和隐藏层神经元数目等)影响,靠经验调参存在一定的局限,所以采用智能算法优化LSTM参数受到研究人员的重视。文献[10]和[19]分别LSTM预测模型对股票和变压器油中溶解气体浓度预测进行预测,并分别采用遗传算法(GA)和粒子群算法(PSO)优化模型的关键参数。本文探索采用1.2节所述的ICS来优化LSTM风速预测模型的关键参数。
4 CS优化LSTM过程
采取CS对LSTM的关键参数进行寻优,流程如下:
- 种群初始化。设置最大迭代次数T、鸟窝数量和概率参数pa。
- 随机化鸟窝位置。以回归均方根误差最小为适应度函数,计算随机鸟窝位置的适应度,得到目前最优鸟窝位置x0b。
- 鸟窝位置更新。依据步长扰动后的鸟窝更新公式(5)更新鸟窝的位置,并计算更新后新一代最优鸟窝。随机产生r∈[0,1],并将r与鸟窝主人可发现外来鸟蛋的概率pa比较,如果r
- 计算新鸟窝的适应度值并更新确定全局最优鸟窝。
- 判断算法是否结束。结束则输出最优时间窗宽TS和隐藏层神经元数目Nn神经元数目;否则回到3)继续搜寻。
二、部分源代码
clear
close all
%% 数据读取
geshu=200;%训练集的个数
%读取数据
shuru=xlsread(‘数据的输入.xlsx’);
shuchu=xlsread(‘数据的输出.xlsx’);
nn = randperm(size(shuru,1));%随机排序
% nn=1:size(shuru,1);%正常排序
input_train =shuru(nn(1:geshu);
input_train=input_train’;
output_train=shuchu(nn(1:geshu);
output_train=output_train’;
input_test =shuru(nn((geshu+1):end);
input_test=input_test’;
output_test=shuchu(nn((geshu+1):end);
output_test=output_test’;
%样本输入输出数据归一化
[aa,bb]=mapminmax([input_train input_test]);
[cc,dd]=mapminmax([output_train output_test]);
global inputn outputn shuru_num shuchu_num
[inputn,inputps]=mapminmax(‘apply’,input_train,bb);
[outputn,outputps]=mapminmax(‘apply’,output_train,dd);
shuru_num = size(input_train,1); % 输入维度
shuchu_num = 1; % 输出维度
%% 利用算法选择最佳的BP参数
N = 4; % 巢穴数量(解决方案的规模)
D = 2 ; % 解的维数
T = 30 ; % 迭代次数
% 自变量上下限
ParticleScope(1,:)=[10 200];
ParticleScope(2,:)=[0.01 0.15];
ParticleScope=ParticleScope’;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
xv=rand(N,D); %首先,初始化种群个体速度和位置
for d=1:D
xv(:,d)=xv(:,d)*(ParticleScope(2,d)-ParticleScope(1,d))+ParticleScope(1,d);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Nest_Pop=xv(:,1:D); % 随机初始解决方案
Pa = 0.25 ; % 建新巢的概率(宿主鸟发现外来鸟蛋后)
for t=1:T
levNestPop = func_levy(Nest_Pop,ParticleScope) ;
% 产生新的解
Nest_Pop = func_bestNestPop(Nest_Pop,levNestPop);
% 在新巢和旧巢中选择一个最好的巢
rand_nestPop = func_newBuildNest(Nest_Pop,Pa,ParticleScope);
% 通过偏好随机游走放弃更糟糕的巢并建立新的巢
Nest_Pop = func_bestNestPop(Nest_Pop,rand_nestPop) ;
% 在新巢和旧巢中选择一个最好的巢
[~,index] = max(func_fitness(Nest_Pop)) ;
% 最好的巢穴
trace(t) = func_objValue(Nest_Pop(index,:)) ;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 参数选择结果赋值
x=Nest_Pop(index,:);
zhongjian1_num = round(x(1));
xue = x(2);
%% 模型建立与训练
options = trainingOptions(‘adam’, … % 梯度下降
‘MaxEpochs’,50, … % 最大迭代次数
‘GradientThreshold’,1, … % 梯度阈值
‘InitialLearnRate’,xue,…
‘Verbose’,0, …
‘Plots’,‘training-progress’); % 学习率
%% 训练LSTM
net = trainNetwork(inputn,outputn,layers,options);
%% 预测
net = resetState(net);% 网络的更新状态可能对分类产生了负面影响。重置网络状态并再次预测序列。
[~,Ytrain]= predictAndUpdateState(net,inputn);
test_simu=mapminmax(‘reverse’,Ytrain,dd);%反归一化
rmse = sqrt(mean((test_simu-output_train).^2)); % 训练集
rmse1 = sqrt(mean((test_simu1-output_test).^2)); % 测试集
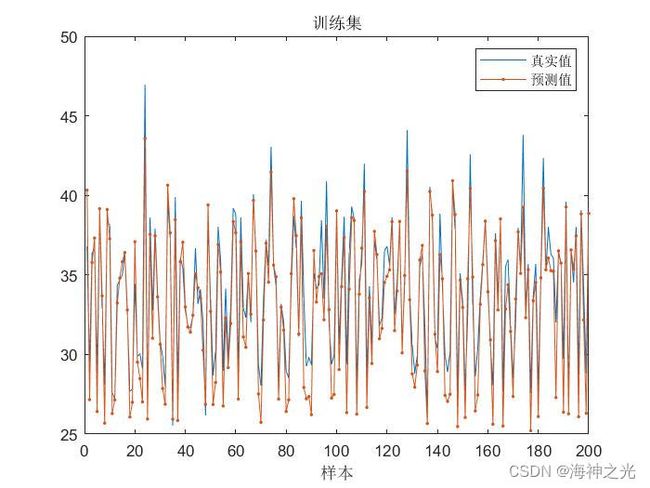
%% 画图
%将预测值与测试数据进行比较。
figure
plot(output_train)
hold on
plot(test_simu,‘.-’)
hold off
legend([“真实值” “预测值”])
xlabel(“样本”)
title(“训练集”)
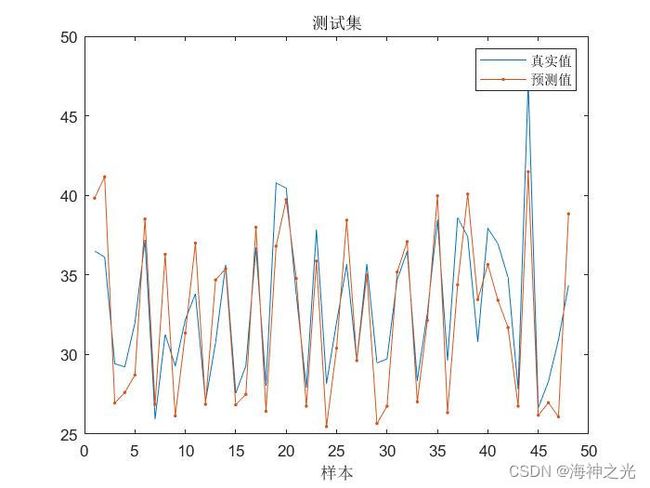
figure
plot(output_test)
hold on
plot(test_simu1,‘.-’)
hold off
legend([“真实值” “预测值”])
xlabel(“样本”)
title(“测试集”)
% 真实数据,行数代表特征数,列数代表样本数output_test = output_test;
T_sim_optimized = test_simu1; % 仿真数据
num=size(output_test,2);%统计样本总数
error=T_sim_optimized-output_test; %计算误差
mae=sum(abs(error))/num; %计算平均绝对误差
me=sum((error))/num; %计算平均绝对误差
mse=sum(error.error)/num; %计算均方误差
rmse=sqrt(mse); %计算均方误差根
% R2=rr;
tn_sim = T_sim_optimized’;
tn_test =output_test’;
N = size(tn_test,1);
R2=(N*sum(tn_sim.*tn_test)-sum(tn_sim)*sum(tn_test))2/((N*sum((tn_sim).2)-(sum(tn_sim))2)*(N*sum((tn_test).2)-(sum(tn_test))^2));
disp(’ ‘)
disp(’----------------------------------------------------------')
disp(['平均绝对误差mae为: ',num2str(mae)])
disp(['平均误差me为: ',num2str(me)])
disp(['均方误差根rmse为: ',num2str(rmse)])
disp(['相关系数R2为: ’ ,num2str(R2)])
三、运行结果
四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 王贺,陈蕻峰,熊敏,刘素梅.融合CEEMDAN和ICS-LSTM的短期风速预测建模[J].电子测量与仪器学报. 2022,36(04)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除