【LSTM回归预测】LSTM神经网络回归预测【含Matlab源码 2227期】

⛄一、时间序列简介

1 时间序列模型概述
1.1 时间序列的不同分类
时间序列是按时间顺序排列的、随时间变化且相互关联的数据序列。分析时间序 列的方法构成数据分析的一个重要领域，即时间序列分析。 时间序列根据所研究的依据不同，可有不同的分类。
（1）按所研究的对象的多少分，有一元时间序列和多元时间序列。
（2）按时间的连续性可将时间序列分为离散时间序列和连续时间序列两种。
（3）按序列的统计特性分，有平稳时间序列和非平稳时间序列。如果一个时间序列的概率分布与时间t无关，则称该序列为严格的（狭义的）平稳时间序列。如果序列的 一、二阶矩存在，而且对任意时刻t满足：
①均值为常数
②协方差为时间间隔 的函数。 则称该序列为宽平稳时间序列，也叫广义平稳时间序列。我们以后所研究的时间序列主 要是宽平稳时间序列。
（3）按时间序列的分布规律来分，有高斯型时间序列和非高斯型时间序列。

确定性时间序列分析方法概述
时间序列预测技术就是通过对预测目标自身时间序列的处理，来研究其变化趋势 的。一个时间序列往往是以下几类变化形式的叠加或耦合。 我们常认为一个时间序列可以分解为以下四大部分：
（1）长期趋势变动。它是指时间序列朝着一定的方向持续上升或下降，或停留在 某一水平上的倾向，它反映了客观事物的主要变化趋势。
（2）季节变动。
（3）循环变动。通常是指周期为一年以上，由非季节因素引起的涨落起伏波形相 似的波动。
（4）不规则变动。通常它分为突然变动和随机变动。

三种时间序列模型

如果在预测时间范围以内，无突然变动且随机变动的方差 \small \sigma ^{2} 较小，并且有理由认 为过去和现在的演变趋势将继续发展到未来时，可用一些经验方法进行预测。

2 移动平均法
移动平均法是根据时间序列资料逐渐推移，依次计算包含一定项数的时序平均数， 以反映长期趋势的方法。当时间序列的数值由于受周期变动和不规则变动的影响，起伏 较大，不易显示出发展趋势时，可用移动平均法，消除这些因素的影响，分析、预测序列的长期趋势。 移动平均法有简单移动平均法，加权移动平均法，趋势移动平均法等。

2.1 简单移动平均法

近N 期序列值的平均值作为未来各期的预测结果。一般 N 的取值范围： 5≤N≤ 200。当历史序列的基本趋势变化不大且序列中随机变动成分较多时，N 的 取值应较大一些。否则 N 的取值应小一些。在有确定的季节变动周期的资料中，移动平均的项数应取周期长度。选择佳 N 值的一个有效方法是，比较若干模型的预测误 差。预测标准误差小者为好。
简单移动平均法只适合做近期预测，而且是预测目标的发展趋势变化不大的情况。 如果目标的发展趋势存在其它的变化，采用简单移动平均法就会产生较大的预测偏差和滞后。

2.2 加权移动平均法
在简单移动平均公式中，每期数据在求平均时的作用是等同的。但是，每期数据所包含的信息量不一样，近期数据包含着更多关于未来情况的信心。因此，把各期数据等同看待是不尽合理的，应考虑各期数据的重要性，对近期数据给予较大的权重，这就 是加权移动平均法的基本思想。

在加权移动平均法中, 的选择，同样具有一定的经验性。一般的原则是：近期 数据的权数大，远期数据的权数小。至于大到什么程度和小到什么程度，则需要按照预 测者对序列的了解和分析来确定。

2.3 趋势移动平均法
简单移动平均法和加权移动平均法，在时间序列没有明显的趋势变动时，能够准确 反映实际情况。但当时间序列出现直线增加或减少的变动趋势时，用简单移动平均法和 加权移动平均法来预测就会出现滞后偏差。因此，需要进行修正，修正的方法是作二次 移动平均，利用移动平均滞后偏差的规律来建立直线趋势的预测模型。这就是趋势移动平均法。 一次移动的平均数为



趋势移动平均法对于同时存在直线趋势与周期波动的序列，是一种既能反映趋势变 化，又可以有效地分离出来周期变动的方法。

3 一般自回归模型 AR(n)
白噪声序列

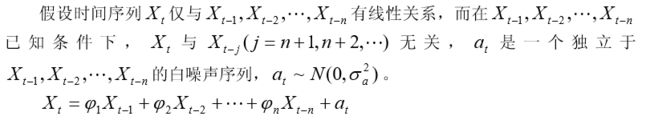
移动平均模型 MA(m)

自回归移动平均模型

ARMA 模型的特性
在时间序列的时域分析中，线性差分方程是极为有效的工具。事实上，任何一个 ARMA 模型都是一个线性差分方程。

AR(1)系统的格林函数
格林函数就是描述系统记忆扰动程度的函数。



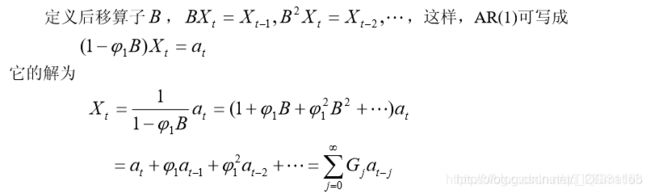
由于格林函数就是差分方程解的系数函数，格林函数的意义可概括如下：

ARMA (2,1)系统的格林函数 的隐式



逆函数和可逆性

4 时间序列建模的基本步骤

⛄二、部分源代码

%% 初始化程序
warning off % 关闭报警信息
close all % 关闭所有图窗
clear % 清空变量
clc % 清空命令行
print_copr; % 版权所有

%% 读取数据
data = xlsread(‘数据集.xlsx’);

%% 划分训练集与测试集
temp = randperm(2000); % 产生1到2000的乱序，用来随机抽取训练集和测试集
inputTrainDataset = data(temp(1:1900), 1:12)‘; % 前1900行数据训练，1到12列为输入变量
outputTrainDataset = data(temp(1:1900), 13)’; % 前1900行数据训练，13列为输出目标

inputTestDataset = data(temp(1901:2000), 1:12)‘; % 1901到2000行数据训练，1到12列为输入变量
outputTestDataset = data(temp(1901 : 2000), 13)’; % 1901到2000行数据训练，13列为输出目标

%% 归一化处理
[inputn_train, input_ps] = mapminmax(inputTrainDataset, 0, 1);
inputn_test = mapminmax(‘apply’, inputTestDataset, input_ps);
[outputn_train, output_ps] = mapminmax(outputTrainDataset, 0, 1);

%% 设置参数
inputnode = length(inputn_train(:, 1)); % 输入层节点
outputnode = 1; % 输出层节点

hiddennode1 = 10; % 第一隐含层节点
hiddennode2 = 20; % 第二隐含层节点

% 创建网络
layers = [ …
sequenceInputLayer(inputnode)
lstmLayer(hiddennode1,‘OutputMode’,‘last’,‘name’,‘hidden1’)
dropoutLayer(0.3,‘name’,‘dropout_1’) %隐藏层1权重丢失率，防止过拟合
lstmLayer(hiddennode2,‘OutputMode’,‘last’,‘name’,‘hidden2’)
dropoutLayer(0.3,‘name’,‘dropout_2’) %隐藏层2权重丢失率，防止过拟合
fullyConnectedLayer(outputnode,‘name’,‘fullconnect’)
regressionLayer(‘name’,‘out’)]; % %回归层

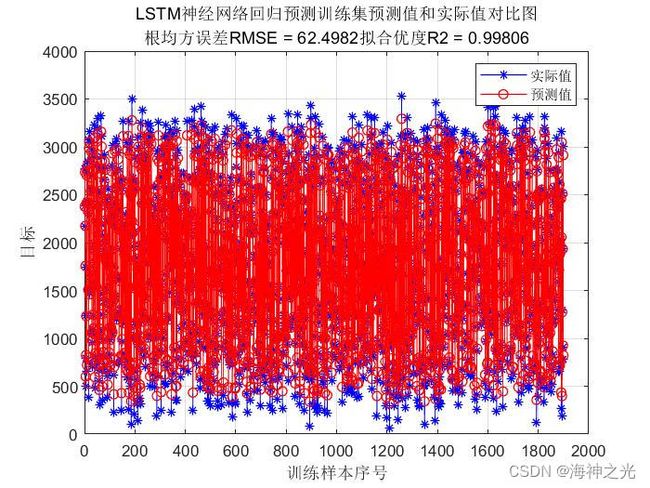
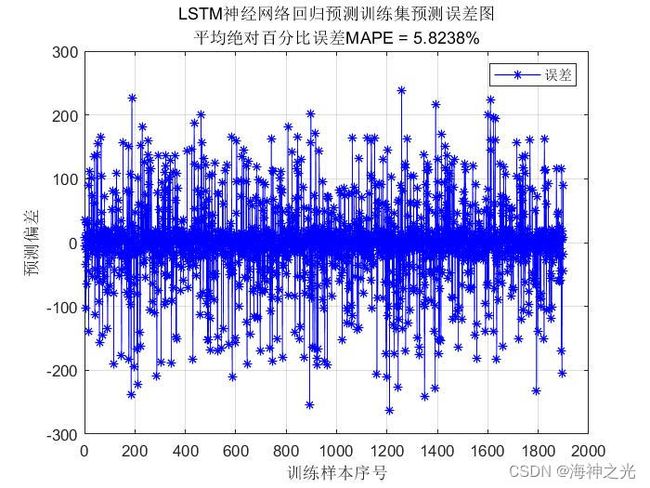
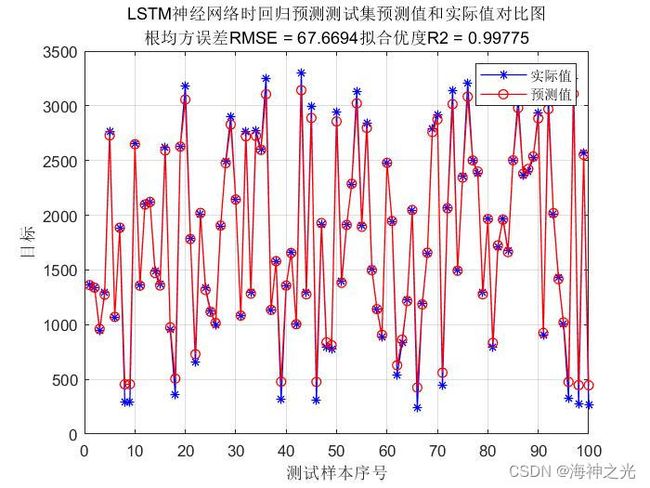
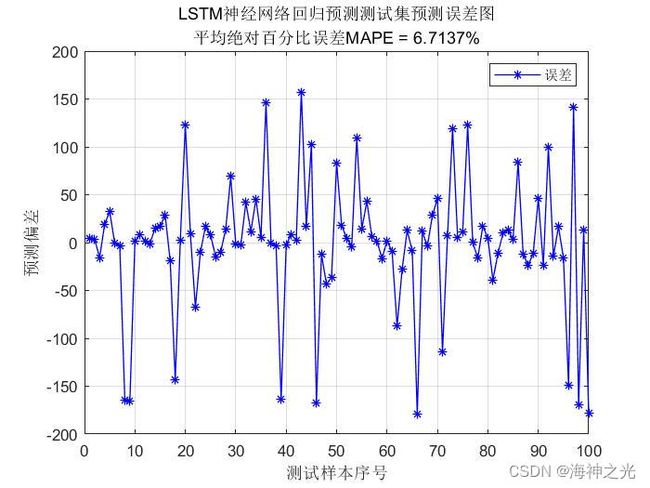
⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]赵明珠,王丹,方杰,李岩,毛军.基于LSTM神经网络的地铁车站温度预测[J].北京交通大学学报. 2020,44(04)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除