机器学习模型常用评价指标（Accuracy, Precision, Recall、F1-score、MSE、RMSE、MAE、R方）

前言

众所周知，机器学习分类模型常用评价指标有Accuracy, Precision, Recall和F1-score，而回归模型最常用指标有MAE和RMSE。但是我们真正了解这些评价指标的意义吗？

在具体场景（如不均衡多分类）中到底应该以哪种指标为主要参考呢？多分类模型和二分类模型的评价指标有啥区别？多分类问题中，为什么Accuracy = micro precision = micro recall = micro F1-score? 什么时候用macro, weighted, micro precision/ recall/ F1-score?

二分类模型常见指标

1. 准确度（accuracy）：

accuracy=$\frac{TP+TN}{TP+FP+TN+FN}$

准确度是指分类正确的预测数与总预测数的比值，准确度越高，分类器越好。

但是准确度并不是一个好指标，因为一旦数据严重不均衡时，accuracy不起作用。比如我们看X光片，真实数据是：99%都是无病的，只有1%是有病的，假设一个分类器只要给它一张X光片，它就判定是无病的，那么它的准确率也有99%，显然这个指标意义不大。当数据异常不平衡时，Accuracy评估方法的缺陷尤为显著。

2. 混淆矩阵

二分类问题中，样本共两种类别：Positive和Negative。当分类器预测结束，我们可以绘制出混淆矩阵（confusion matrix）。其中分类结果分为如下几种：

	Actual Positive	Actual Negative
Predicted Positive	TP	FP
Predicted Negative	FN	TN

• True Positive (TP): 把正样本成功预测为正。
• True Negative (TN)：把负样本成功预测为负。
• False Positive (FP)：把负样本错误地预测为正。
• False Negative (FN)：把正样本错误的预测为负。

在二分类模型中，Accuracy（准确率）、Precision（精确率）、Recall（召回率）和F1 score的定义如下：

Accuracy=$\frac{TP+TN}{TP+FP+TN+FN}$

Precision=$\frac{TP}{TP+FP}$

Recall=$\frac{TP}{TP+FN}$

F1-score=$\frac{2\ast Precision\ast Recall}{Precision+Recall}$

其中，Precision着重评估在预测为Positive的所有数据中，真实Positive的数据到底占多少？Recall着重评估在所有的真实Positive数据中，到底有多少数据被成功预测为Positive？

举个例子，一个医院新开发了一套癌症AI诊断系统，想评估其性能好坏。我们把病人得了癌症定义为Positive，没得癌症定义为Negative。那么， 到底该用什么指标进行评估呢？

如果用Precision对系统进行评估，那么其回答的问题就是：

在诊断为癌症的一堆人中，到底有多少人真得了癌症？

如果用Recall对系统进行评估，那么其回答的问题就是：

在一堆得了癌症的病人中，到底有多少人能被成功检测出癌症？

如用Accuracy对系统进行评估，那么其回答的问题就是：

在一堆癌症病人和正常人中，有多少人被系统给出了正确诊断结果（患癌或没患癌）？

精准率和召回率之间是互相矛盾的，如果提高召回率，精准率就不可避免的下降，如果精准率提高，召回率就不可避免的下降。那什么时候注重Precision还是Recall？

在稳定TP的情况下，主要是更关注FP和FN的哪一个。以垃圾邮件屏蔽系统为例，垃圾邮件为Positive，正常邮件为Negative，False Positive是把正常邮件识别为垃圾邮件，这种情况是最应该避免的（你能容忍一封重要工作邮件直接进了垃圾箱，被不知不觉删除吗？）。我们宁可把垃圾邮件标记为正常邮件 (FN)，也不能让正常邮件直接进垃圾箱 (FP)。在这里，垃圾邮件屏蔽系统的目标是：尽可能提高Precision值，哪怕牺牲一部分Recall。

F1 score是Precision和Recall两者的综合（调和平均数），主要用途来比较两个分类器的性能，取值范围为0到1，数值越大越好；

多分类模型常见指标

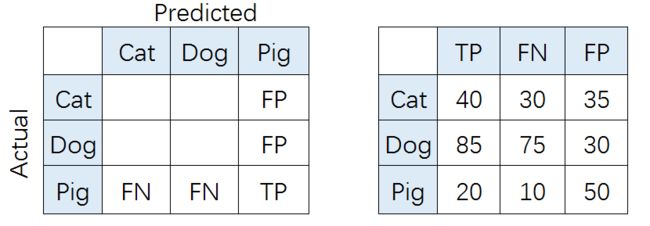
在多分类（大于两个类）问题中，假设我们要开发一个动物识别系统，来区分输入图片是猫，狗还是猪。给定分类器一堆动物图片，产生了如下结果混淆矩阵。

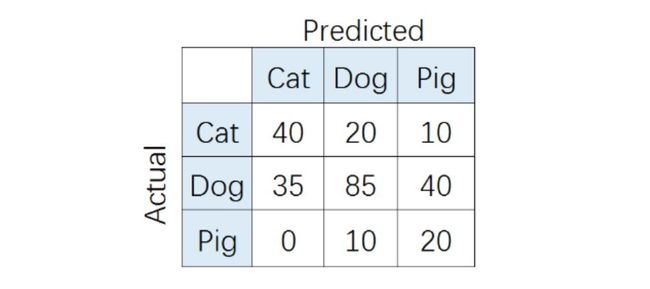
在混淆矩阵中，正确的分类样本（Actual label = Predicted label）分布在左上到右下的上对角线上。其中，Accuracy的定义为分类正确（对角线上）的样本数与总样本数的比值。Accuracy度量的是全局样本预测情况。而对于Precision和Recall而言，每个类都需要单独计算其Precision和Recall。

比如，对类别「猪」而言，其Precision和Recall分别为:

Precision=$\frac{TP}{TP+FP}$=$\frac{20}{20+50}$=$\frac{2}{7}$

Recall=$\frac{TP}{TP+FN}$=$\frac{20}{20+10}$=$\frac{2}{3}$

也就是，

$P_c$=$\frac{8}{15}$,$P_d$=$\frac{17}{23}$,$P_p$=$\frac{2}{7}$（P代表Precision）

$R_c$=$\frac{4}{7}$,$R_d$=$\frac{17}{32}$,$R_p$=$\frac{2}{3}$（R代表Recall）

如果想评估该识别系统的总体功能，必须考虑猫、狗、猪三个类别的综合预测性能。那么，到底要怎么综合这三个类别的Precision呢？是简单加起来做平均吗？通常来说， 我们有如下几种解决方案（也可参考scikit-learn官网）：

1. Macro-average方法
   该方法最简单，直接将不同类别的评估指标（Precision/ Recall/ F1-score）加起来求平均，给所有类别相同的权重。该方法能够平等看待每个类别，但是它的值会受稀有类别影响。

Macro-average=$\frac{P_c+P_d+P_p}{3}$=0.5194

Macro-average=$\frac{R_c+R_d+R_p}{3}$=0.5898

2. Weighted-average方法

该方法给不同类别不同权重（权重根据该类别的真实分布比例确定），每个类别乘权重后再进行相加。该方法考虑了类别不平衡情况，它的值更容易受到常见类（majority class）的影响。

$W_c$:$W_d$:$W_p$=$N_c$:$N_d$:$N_p$=$\frac{7}{26}$:$\frac{16}{26}$:$\frac{3}{26}$ (W代表权重，N代表样本在该类别下的真实数目)

Weighted-average=$P_c\ast W_C+P_d\ast W_d+P_p\ast W_p$=0.6314

Weighted-average=$R_c\ast W_C+R_d\ast W_d+R_p\ast W_p$=0.5577

3. Micro-average方法

该方法把每个类别的TP, FP, FN先相加之后，在根据二分类的公式进行计算。

Micro-average=$\frac{T{P}_c+T{P}_d+T{P}_p}{T{P}_c+T{P}_d+T{P}_p+F{P}_c+F{P}_d+F{P}_p}$=0.5577

Micro-average=$\frac{T{P}_c+T{P}_d+T{P}_p}{T{P}_c+T{P}_d+T{P}_p+F{N}_c+F{N}_d+F{N}_p}$=0.5577

其中，特别有意思的是，Micro-precision和Micro-recall竟然始终相同！这是为啥呢？

这是因为在某一类中的False Positive样本，一定是其他某类别的False Negative样本。听起来有点抽象？举个例子，比如说系统错把「狗」预测成「猫」，那么对于狗而言，其错误类型就是False Negative，对于猫而言，其错误类型就是False Positive。于此同时，Micro-precision和Micro-recall的数值都等于Accuracy，因为它们计算了对角线样本数和总样本数的比值，总结就是：

Micro Precision = Micro Recall = Micro F1-score=Accuracy

二分类实现

from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_log_predict)

from sklearn.metrics import precision_score
precision_score(y_test, y_log_predict)

from sklearn.metrics import recall_score
recall_score(y_test, y_log_predict)

from sklearn.metrics import f1_score
f1_score(y_test, y_predict)

注意：
1.预测值在后面，标签值在前面；
2.多分类问题需要添加指标计算方法，二分类时average参数默认是binary；多分类时，可选参数有micro、macro、weighted和samples
报错信息：python编译报错 Target is multiclass but average=‘binary’. Please choose another average setting
from sklearn.metrics import precision_score, recall_score
修改后代码：precision_score(y_train, y_train_pred, average=‘micro’)

回归模型常用指标

对于简单线性回归，目标是找到a,b 使得${\sum }_{i=1}^m(y^i-a\ast x^i-b{)}^2$尽可能小,

其实相当于是对训练数据集而言的，即${\sum }_{i=1}^m(y^i-y_t^i{)}^2$尽可能小,

但问题是，这个衡量标准和m相关。当10000个样本误差累积是100，而另一个800个样本误差累积却达到了80，虽然80<100，但我们却不能说第二个模型优于第一个.

1. 均方误差（MSE）:对式子除以m，使得其与测试样本m无关

$$\frac{1}{m}\sum _{i=1}^m(y^i-y_t^i{)}^2$$

但又有一个问题，之前算这个公式时为了保证其每项为正，且可导（所以没用绝对值的表示方法），我们对式子加了一个平方。但这可能会导致量纲的问题，如房子价格为万元，平方后就成了万元的平方。

2. 均方根误差（RMSE）:对MSE开方，使量纲(单位)相同

$$\frac{1}{m}\sum _{i=1}^m\sqrt{(y^i-y_t^i{)}^2}$$

注：MSE与RMSE的区别仅在于对量纲是否敏感

3. 平均绝对误差：通过加绝对值作差

$$\frac{1}{m}\sum _{i=1}^m(|y^i-y_t^i)|$$

在推导a,b的式子时（对train数据集），没用求绝对值的方法是因为其不是处处可导，不方便用来求极值。但评价模型时，对test数据集我们完全可以使用求绝对值的方式。

P.S. 评价模型的标准和训练模型时最优化的目标函数是可以完全不一样的。

RMSE vs MAE

RMSE 与 MAE 的量纲相同，但求出结果后我们会发现RMSE比MAE的要大一些。这是因为RMSE是先对误差进行平方的累加后再开方，它其实是放大了较大误差之间的差距。而MAE反应的就是真实误差。因此在衡量中使RMSE的值越小其意义越大，因为它的值能反映其最大误差也是比较小的。

对于上述的衡量方法，如RMSE和MAE还是有问题的，还是因为量纲不一样。比如我们预测考试分数误差是10，预测房价误差是1w。但我们却不能评价我们的模型是更适合预测分数还是预测房价。

4. R Squared
   
   （上：y预测-y真，our model，下：y真平均-y真，baseline model）

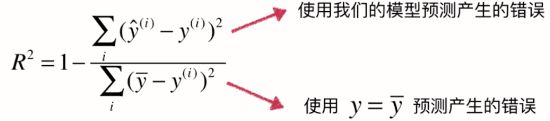
可以把公式理解为1 - ourModelError / baselineModelError = 我们模型拟合住的部分。R方将回归结果归约到了0~1间，R方越大越好，允许我们对不同问题的预测结果进行比对了。

文章出处：
1.https://zhuanlan.zhihu.com/p/147663370
2.https://www.cnblogs.com/zzzzy/p/8490662.html