Pytorch自动求梯度
求梯度
- 微分
- Pytorch自动微分
微分
通常我们见到的微分方法有两种:
·符号微分法:
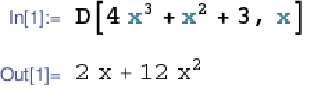
·数值微分法:
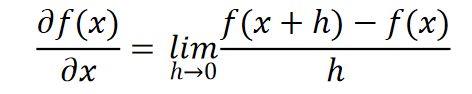
Pytorch自动微分
对于一个Tensor,如果它的属性requires_grad 设置为 True,它将开始追
踪(track)在其上的所有操作
我们定义一个初始的tensor并且requires_grad 设置为 True:
x = torch.ones(2, 2, requires_grad=True)
print(x)
tensor([[1., 1.],
[1., 1.]], requires_grad=True)
此时,我们在x的基础上进行运算:
y = x + 2
print(y)
tensor([[3., 3.],
[3., 3.]], grad_fn=<AddBackward0>)
# grad_fn属性代表y是否由运算得来
此时我们就可以进一步运算:out =(x+2)**2
z = y * y * 3
out = z.mean()
print(z, out)
反向传播:
out.backward() # 等价于 out.backward(torch.tensor(1.))
此时我们就可以输出x的梯度:
print(x.grad)
注意:grad在反向传播过程中是累加的(accumulated),这意味着每⼀次运⾏反向传播,梯度都会累加之前的梯度,所以⼀般在反向传播之前需把梯度清零
tensor([[4.5000, 4.5000],
[4.5000, 4.5000]])
为什么会输出这个值呢?接下来看一下过程:
我们可以写出out的等式:
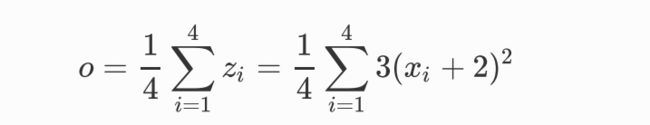
此时我们求o关于x的偏导:
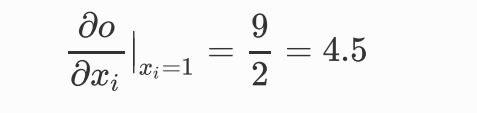
那么我们在在进行求梯度时为什么要求out的梯度呢?为什么最后要z.mean()呢?
很显然我们直接y.backward()会报错
这是因为:在 y.backward() 时,如果 y 是标量,则不需要为 backward() 传⼊任何参数;否则,需要传⼊⼀个与 y 同形的 Tensor 。
在pytorch中:不允许张量对张量求导,只允许标量对张量求导,求导结果是和⾃变量同形的张量。所以必要时我们要把张量通过将所有张量的元素加权求和的方式转换为标量
接下来看一个实际的栗子:
x = torch.tensor([1.0, 2.0, 3.0, 4.0], requires_grad=True)
y = 2 * x
print(y)
tensor([2., 4., 6., 8.], grad_fn=<MulBackward0>)
此时我们直接y.backward()会报错,因为y不是标量,所以我们按照要求应该传入一个同形的张量,作为权重:
t = torch.tensor([1,2,3,4])
y.backward(t)
print(x.grad)
d(y) = 2
求导的同时也应该乘以相应的权重t = torch.tensor([1,2,3,4]),所以最后输出:
tensor([2., 4., 6., 8.])
喜欢文章可以点赞收藏,欢迎关注,如有错误请指正!