【从零开始学习深度学习】38. Pytorch实战案例:梯度下降、随机梯度下降、小批量随机梯度下降3种优化算法对比【含数据集与源码】
本文将使用一个来自NASA测试不同飞机机翼噪音的数据集,通过梯度下降、随机梯度下降、小批量随机梯度下降这3种优化算法进行模型训练,比较3种训练结果的差异。
目录
- 1. 梯度下降、随机梯度下降、小批量随机梯度下降区别
- 2. 读取训练数据
- 3. 从零实现3种梯度算法并进行训练
-
- 3.1 梯度下降训练结果
- 3.2 随机梯度下降将结果
- 3.3 小批量随机梯度下降结果
- 4 .使用Pytorch的optim.SGD实现梯度下降优化算法
-
- 4.1 梯度下降训练结果
- 4.2 随机梯度下降将结果
- 4.3 小批量随机梯度下降结果
- 5. 总结
1. 梯度下降、随机梯度下降、小批量随机梯度下降区别
梯度下降:在每一次迭代中,梯度下降使用整个训练数据集来计算梯度,一个epoch周期内参数只更新一次。
随机梯度下降:在每次迭代中,只随机采样一个样本来计算梯度,一个epoch周期内会进行样本数目次参数更新。
小批量随机梯度下降:在每次迭代中随机均匀采样多个样本来组成一个小批量来计算梯度,一个epoch周期内会进行(样本数目/批量大小)次的参数更新。
2. 读取训练数据
获取数据集方法,关注GZH:阿旭算法与机器学习,回复“梯度下降”即可。
该数据集为NASA的测试不同飞机机翼噪音的数据集,数据集一共包含1503个样本,每个样本包含5个特征与1个标签,下面我们将使用该数据集的前1,500个样本进行模型的训练,并比较各个优化算法的区别。
数据集展示:
%matplotlib inline
import numpy as np
import time
import torch
from torch import nn, optim
import sys
import d2lzh_pytorch as d2l
def get_data_ch7():
data = np.genfromtxt('./data/airfoil_self_noise.dat', delimiter='\t')
# 标准化数据
data = (data - data.mean(axis=0)) / data.std(axis=0)
return torch.tensor(data[:1500, :-1], dtype=torch.float32), \
torch.tensor(data[:1500, -1], dtype=torch.float32) # 前1500个样本(每个样本包含5个特征)
features, labels = get_data_ch7()
features.shape # torch.Size([1500, 5])
3. 从零实现3种梯度算法并进行训练
下面实现一个通用的训练函数,它初始化一个线性回归模型,然后可以使用梯度下降、随机梯度下降和小批量随机梯度下降算法来训练模型。
# 参数优化器
def sgd(params, states, hyperparams):
for p in params:
p.data -= hyperparams['lr'] * p.grad.data
# 训练函数
def train_ch7(optimizer_fn, states, hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型,初始化一个线性回归模型
net, loss = d2l.linreg, d2l.squared_loss
w = torch.nn.Parameter(torch.tensor(np.random.normal(0, 0.01, size=(features.shape[1], 1)), dtype=torch.float32),
requires_grad=True)
b = torch.nn.Parameter(torch.zeros(1, dtype=torch.float32), requires_grad=True)
def eval_loss():
return loss(net(features, w, b), labels).mean().item()
ls = [eval_loss()]
data_iter = torch.utils.data.DataLoader(
torch.utils.data.TensorDataset(features, labels), batch_size, shuffle=True)
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
l = loss(net(X, w, b), y).mean() # 使用平均损失
# 梯度清零
if w.grad is not None:
w.grad.data.zero_()
b.grad.data.zero_()
l.backward()
optimizer_fn([w, b], states, hyperparams) # 迭代模型参数
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss()) # 每100个样本记录下当前训练误差
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
d2l.set_figsize()
d2l.plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
d2l.plt.xlabel('epoch')
d2l.plt.ylabel('loss')
3.1 梯度下降训练结果
当批量大小为样本总数1,500时,使用的是梯度下降。梯度下降的1个迭代周期对模型参数只迭代1次。可以看到6次迭代后目标函数值(训练损失)的下降趋向了平稳。
def train_sgd(lr, batch_size, num_epochs=2):
train_ch7(sgd, None, {'lr': lr}, features, labels, batch_size, num_epochs)
train_sgd(1, 1500, 6)
输出:
loss: 0.245426, 0.013536 sec per epoch
3.2 随机梯度下降将结果
当批量大小为1时,优化使用的是随机梯度下降。随机梯度下降中,每处理一个样本会更新一次自变量(模型参数),一个迭代周期里会对自变量进行1,500次更新。可以看到,目标函数值的下降在1个迭代周期后就变得较为平缓。
train_sgd(0.005, 1)
输出:
loss: 0.246051, 0.531435 sec per epoch
虽然随机梯度下降和梯度下降在一个迭代周期里都处理了1,500个样本,但实验中随机梯度下降的一个迭代周期耗时更多。这是因为随机梯度下降在一个迭代周期里做了更多次的自变量迭代,而且单样本的梯度计算难以有效利用矢量计算。
3.3 小批量随机梯度下降结果
当批量大小为10时,优化使用的是小批量随机梯度下降。它在每个迭代周期的耗时介于梯度下降和随机梯度下降的耗时之间。
train_sgd(0.05, 10)
输出:
loss: 0.242805, 0.078792 sec per epoch
4 .使用Pytorch的optim.SGD实现梯度下降优化算法
在PyTorch里可以直接通过创建optimizer实例来调用优化算法。这能让实现更简洁。下面实现一个通用的训练函数,它通过优化算法的函数optimizer_fn和超参数optimizer_hyperparams来创建optimizer实例。
def train_pytorch_ch7(optimizer_fn, optimizer_hyperparams, features, labels,
batch_size=10, num_epochs=2):
# 初始化模型
net = nn.Sequential(
nn.Linear(features.shape[-1], 1)
)
loss = nn.MSELoss()
optimizer = optimizer_fn(net.parameters(), **optimizer_hyperparams)
def eval_loss():
return loss(net(features).view(-1), labels).item() / 2
ls = [eval_loss()]
data_iter = torch.utils.data.DataLoader(
torch.utils.data.TensorDataset(features, labels), batch_size, shuffle=True)
for _ in range(num_epochs):
start = time.time()
for batch_i, (X, y) in enumerate(data_iter):
# 除以2是为了和train_ch7保持一致, 因为squared_loss中除了2
l = loss(net(X).view(-1), y) / 2
optimizer.zero_grad()
l.backward()
optimizer.step()
if (batch_i + 1) * batch_size % 100 == 0:
ls.append(eval_loss())
# 打印结果和作图
print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
d2l.set_figsize()
d2l.plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
d2l.plt.xlabel('epoch')
d2l.plt.ylabel('loss')
下面重复第3小节中的实验。
4.1 梯度下降训练结果
train_pytorch_ch7(optim.SGD, {"lr": 0.05}, features, labels, batch_size=1500, num_epochs=6)
输出:
loss: 0.701703, 0.013035 sec per epoch
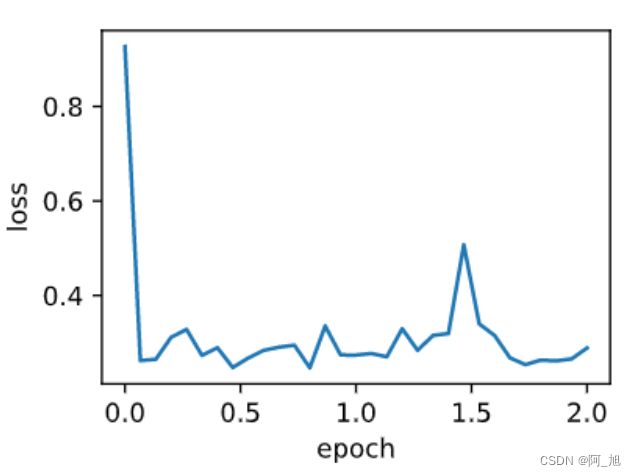
4.2 随机梯度下降将结果
train_pytorch_ch7(optim.SGD, {"lr": 0.05}, features, labels, batch_size=1, num_epochs=2)
输出:
loss: 0.288860, 0.586868 sec per epoch
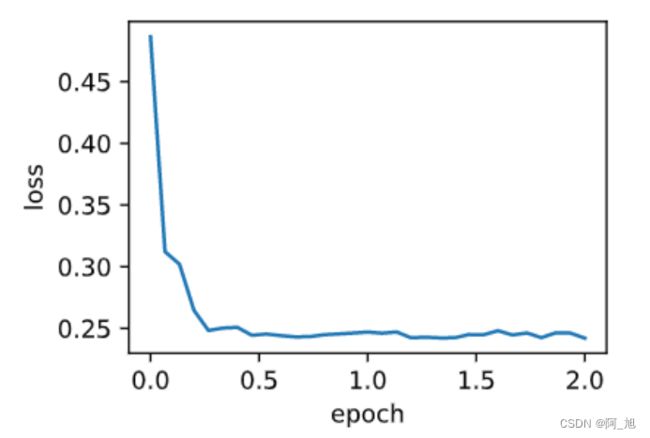
4.3 小批量随机梯度下降结果
train_pytorch_ch7(optim.SGD, {"lr": 0.05}, features, labels, batch_size=10, num_epochs=2)
输出:
loss: 0.242063, 0.075203 sec per epoch
5. 总结
- 小批量随机梯度每次随机均匀采样一个小批量的训练样本来计算梯度。
- 通常,小批量随机梯度在每个迭代周期的耗时介于梯度下降和随机梯度下降的耗时之间。
如果文章内容对你有帮助,感谢点赞+关注!
关注下方GZH:阿旭算法与机器学习,回复:“梯度下降”即可获取本文数据集、源码与项目文档,欢迎共同学习交流