《Learning from Protein Structure with Geometric Vector Perceptrons》文献阅读

本博文基于《Learning from Protein Structure with Geometric Vector Perceptrons》进行翻译讲解，该文章发表于2021年的ICLR，作者来自斯坦福大学。该文章认为大型生物分子的三维结构学习是机器学习的一个独特领域，但是还没有出现一个统一的网络架构，同时利用问题领域的几何和关系两个层面。为了解决这个问题，作者引入了几何向量感知器，它扩展标准的密集层来操作欧几里德向量集合。配有几何向量感知器之后，图神经网络能够执行几何和关系推理，得到大分子的有效表示。作者在从蛋白质结构学习的两个重要问题上展示了他们的方法: 模型质量评估和计算蛋白质设计。他们的方法在这两个问题上都优于现有的架构，包括最先进的卷积神经网络和图神经网络。论文的代码公开在https://github.com/drorlab/gvp上。

一、任务背景

结构生物学的许多努力都是为了预测或者从一个大分子（例如蛋白质、RNA 或者DNA）的结构中获得启示，这些大分子在三维欧几里德空间中表现为一系列与原子或原子群相关的位置。这些问题通常可以被定义为将结构的输入域映射到某种感兴趣的性质的函数ーー例如，预测结构模型的质量，或者确定两个分子是否会在特定的几何形状中结合。由于它们的重要性和困难性，这些问题，我们广泛地称之为从结构中学习，最近已经发展成为深度学习一个有前景的应用领域。
深度学习的成功应用通常是由利用领域问题结构的技术驱动的ー例如计算机视觉中的卷积和自然语言处理中的注意力。从结构中学习的相关考虑是什么？以蛋白质为最常见的例子，我们一方面了解氨基酸残基在空间中的排列和方向，这些氨基酸残基控制着分子的动力学和功能。另一方面，蛋白质在其氨基酸序列和残基-残基相互作用方面也具有相关结构，这些相互作用产生了上述的蛋白质性质。我们把这些分别称为问题域的几何和关系两个层面。
近来最先进的模型在结构学习上利用了这两个层面中的一个。通常，这些方法使用图神经网络(GNNs) ，这是表达了关系推理，或卷积神经网络(CNNs) ，这是在几何结构上的操作。作者提供了一个统一的体系结构，该体系结构连接了CNNs和GNNs两种方法来利用问题领域的两个层面。
作者通过引入几何向量感知机(Geometric Vector Perceptrons, GVPs)来实现这一点，这是一种在 GNNs的聚合和前馈层中替代标准多层感知器(MLPs)的方法。GVPs 直接操作标量和几何特征——在空间坐标旋转下转换为矢量特征。因此，GVP允许在节点和边中嵌入几何信息，而不会将此类信息减少为可能无法完全捕获复杂几何体的标量。作者假设他们的方法使GNN更容易学习其重要特征是几何和关系的函数。
作者提出的方法（GVP-GNN）可以应用于任何输入域是单个大分子或相互结合的分子结构的问题。在这项工作中，作者特别演示了他们在蛋白质结构的两个相关问题上的方法: 计算蛋白质设计和模型质量评估。计算蛋白质设计（Computational protein design, CPD）是蛋白质结构预测的概念反转，旨在推断将折叠成给定结构的氨基酸序列。模型质量评估(Model quality assessment, MQA)旨在从大量的候选结构中选择蛋白质的最佳结构模型，是结构预测的重要步骤。作者提出的方法在这两个任务上都优于现有的方法。

二、相关工作

从蛋白质结构中学习的ML方法主要分为三种类型，分别是对蛋白质的序列表示、体素表示或图结构表示。作者简要讨论每种类型，并介绍MQA和CPD的最先进的示例，为以后的实验奠定基础。
序列表示（Sequential representations）：在传统的蛋白质结构学习模型中，每种氨基酸都是用手工制作的3D结构环境表示法表示为一个特征向量。这些表征包括残基接触，集体投影到局部坐标的方向或位置，物理激发的能量项，或蛋白质拓扑的上下文无关语法。然后将该结构视为这些特征的序列或集合，这些特征可以馈入一维卷积网络、RNN或密集前馈网络。虽然这些方法仅间接代表蛋白质的完整3D结构，但其中一些方法，如ProQ4、VoroMQA和SBROD，在MQA评估中具有竞争力。
体素化表示（Voxelized representations）：3D卷积神经网络（CNN）可以代替手工制作的结构表示，直接对空间中的原子位置进行操作，在体素化3D体积中编码为占用图。这种网络的层次卷积很容易与结构基序、绑定口袋和其他重要结构特征的特定形状的检测兼容，利用了域的几何方面。在许多CPD和MQA上，3DCNN和Ornate都证明了该方法的强大。
图结构表示（Graph-structured representations）：蛋白质结构也可以表示为氨基酸节点上的邻接图，从而将在单个特征向量中表示集体结构邻域的挑战减少到表示单个边的挑战。然后，图神经网络（GNN）可以对结构进行复杂的关系推理——例如，识别氨基酸之间的关键关系，或描述为连接性模式而非刚性形状的柔性结构基序。最近最先进的GNN包括CPD上的Structured Transformer、CPD和突变稳定性预测上的ProteinSover以及MQA上的GraphQA。这些方法在几何图形的表示上各不相同：有些方法（如ProteinSover和GraphQA）将边表示为其长度的函数，而另一些方法（如Structured Transformer）则根据相对方向和其他标量特征间接对邻近图的三维几何图形进行编码。

三、方法

作者的模型架构旨在通过提高CNN和GNN方法从生物分子结构中学习的能力，从而结合CNN和GNN方法的优点。前一节中描述的GNN通过按照旋转不变量标量编码向量特征（如节点方向和边方向），通常通过在每个节点定义局部坐标系，对蛋白质的3D几何结构进行编码。然而，作者建议将这些特征直接表示为3D几何向量特征，这些特征在图传播的所有步骤中，在空间坐标的变化下进行适当的变换。
这种观念上的转变有两个重要结果。首先，输入表示更有效：不需要通过节点与其所有邻居的相对方向来编码节点的方向，而只需要为每个节点表示一个绝对方向。其次，它标准化了整个结构的全局坐标系，允许几何特征直接传播，而无需在局部坐标之间转换。例如，空间中任意位置的表示，包括本身不是节点的点，可以通过欧几里德向量加法轻松地在图中传播。假设这使得GNN更容易访问结构的全局几何特性。然而，这种表示法的关键挑战是，在保持标量表示法提供的旋转不变性的同时，以一种同时保留原始GNN的全部表达能力的方式执行图传播。为此，我们引入了一个新的模块，几何向量感知机(GVPs)，以取代GNN中的密集层。

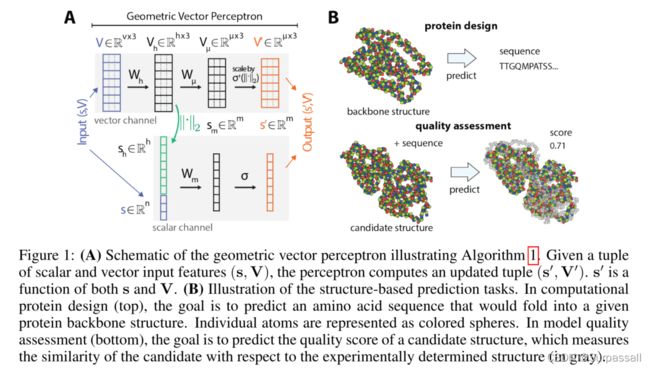
1 几何向量感知机

几何向量感知机（GVPs）是一个简单的模块，用于学习几何向量和标量上的向量值函数和标量值函数。给定一个元组$(\mathbf{s},\mathbf{V})$，其中标量特征$\mathbf{s}\in {\mathbb{R}}^n$，向量特征$\mathbf{V}\in {\mathbb{R}}^{v\times 3}$，计算新特征$(\mathbf{s},\mathbf{V})\in {\mathbb{R}}^m\times {\mathbb{R}}^{\mu \times 3}$。计算的过程被展示在图1A和描述在算法1中。

在GVPs的核心中，包含两个线性变换的矩阵，分别是用于标量特征变换的${\mathbf{W}}_m$和用于向量特征变换的${\mathbf{W}}_h$，紧接着跟着两个非线性函数$\sigma$和${\sigma }^{+}$，非线性${\sigma }^{+}$是应用于$L_2$范数的${\sigma }^{+}$的缩放。然而，在标量特征被转换之前，作者拼接了转换后的特征向量${\mathbf{V}}_h$的$L_2$正则，这能从输入向量$\mathbf{V}$提取到旋转不变性的信息。在向量非线性之前插入一个额外的线性变换${\mathbf{W}}_{\mu }$，以独立于提取的范数控制输出维数。
GVP在概念上很简单，但可以证明它具有不变性/等变性和表达性。首先，GVP的矢量输出和标量输出对于三维欧氏空间中旋转和反射的任意合成 $R$ 分别是等变和不变的——即，$GVP(\mathbf{s},\mathbf{V})=({\mathbf{s}}^{\prime },{\mathbf{V}}^{\prime })$，则有
$$GVP(\mathbf{s},R(\mathbf{V}))=({\mathbf{s}}^{\prime },R({\mathbf{V}}^{\prime }))\text{\hspace{1em}(1)}$$
这是因为对向量值输入的唯一操作是标量乘法、线性组合和L2范数。作者在附录A中提供了正式证明。
下面的截图是作者在论证GVP体系结构可以逼近$\mathbf{V}$的任何连续旋转和反射不变标量值函数，有点偏数学，比较难懂，这里不过多阐述。

作者研究了GVPs增强GNNs在人造模拟数据集上的几何推理能力的假设（附录B）。人造模拟数据集允许控制基础真值标签下的函数，以便在不同任务中显式分离几何和关系两个层面。GVP增强GNN（或GVP-GNN）在几何任务上匹配CNN，在关系任务上匹配标准GNN。然而，当作者将这两项任务结合在一个目标中时，GVP-GNN比GNN或CNN都要好得多。

2 蛋白质的表示

作者的体系结构的主要经验验证是它在两个实际任务上的性能：计算蛋白质设计(CPD)和模型质量评估(MQA)。这些任务，如图1b 所示，并在第4节详细描述，是互补的，其中一个(CPD)预测每个氨基酸的属性，而另一个(MQA)预测全局属性。
作者将一个蛋白质结构输入表示为一个邻接图，带有最少数量的标量和向量特征，以指定分子的三维结构。蛋白质结构是一个氨基酸序列，其中每个氨基酸由四个主干原子和一组位于三维欧氏空间的侧链原子组成。作者只表示主干，因为侧链在CPD中是未知的，并且MQA基准只对应于主干结构的评估。
作者将蛋白质的主干部门表示成一个图$G=(\nu ,\epsilon )$，每个点${\nu }_i$对应一个氨基酸，并且有一个embedding ${\mathbf{h}}_{\nu }^{(i)}$，该embedding具有如下特征：

同样地，边的集合表示为$\epsilon =\{e_{j\to i}{\}}_{i\ne j}$，每条边都有对应的embedding ${\mathbf{h}}_{\mathbf{e}}^{(j\to i)}$，具有如下特征：

在所有符号中，每个特征向量 $\mathbf{h}$ 都是上面描述的标量和矢量特征的串联。总的来说，这些特征足以完整描述蛋白质主干。

3 网络架构

作者的架构（GVP-GNN）利用了消息传递，其中来自相邻节点和边的消息用于在每个图传播步骤更新节点嵌入。更明确地说，该架构采用上面定义的蛋白质图作为输入，并根据以下步骤执行图传播步骤:

其中，$g$是三个GVPs的叠加函数，${\mathbf{h}}_{\mathbf{m}}^{(j\to i)}$表示从节点 $i$ 到节点 $j$ 传递的信息。$k^{\prime }$表示邻接信息节点的数量，它是等于上一节提到的 $k$ ，除非蛋白质本身少于 $k$ 个氨基酸。
在图传播步骤之间，作者还使用前馈逐点层更新所有节点 $i$ 的节点嵌入：

其中，$g$是两个GVPs的叠加函数。这些图传播和前馈步骤除了更新每个节点的标量特征之外，还更新了其向量特征。
在计算蛋白质设计中，网络根据给定的主干结构在蛋白质序列的空间上学习生成模型。在 Ingraham 等人(2019)之后，作者将其框架视为为一个自回归任务，并使用一个掩码编-解码器结构来捕获所有位置的联合分布：对于每一个 $i$ ，网络基于完整的结构图以及位置$j<i$处的序列信息对 $i$ 处的分布进行建模。编码器首先只对结构信息执行三个图传播步骤。然后，序列信息被添加进图中，解码器执行三个进一步的图传播步骤，其中，收到的信息${\mathbf{h}}_{\mathbf{m}}^{(j\to i)}$只用编码器的embedding来计算。最后，作者使用最后一个具有20-way标量softmax输出的GVP来预测氨基酸的概率。
在模型质量评估中，作者使用三个图传播步骤，并对候选结构的真实质量分数进行回归，这是一个全局标量属性。为了获得一个单一的全局表示，作者应用一个基于节点的GVP将所有节点embedding减少到标量。然后，对所有节点的表示进行平均，并应用最终的密集前馈网络来输出网络的预测。
有关训练和超参数的更多详细信息，请参见附录D。

四、评价指标和数据集

蛋白质设计：计算蛋白质设计（CPD）是蛋白质结构预测的概念反转，旨在推断将折叠成给定结构的氨基酸序列。CPD很难直接进行基准测试，因为一些结构可能对应于大空间的序列，而另一些结构可能根本不对应。因此，通常使用原生序列恢复（native sequence recovery）的代理指标，根据实验确定的结构推断原生序列。Ingraham等人在序列设计和语言建模之间进行了类比，并评估了序列的模型困惑度（perplexity）。这两个指标都基于一个隐含的假设，即原本的序列针对其结构进行了优化，并且应该被赋予高概率。
为了最好地逼近可能需要设计新结构的实际应用，所提出的评测集应与训练结构具有最小的相似性。作者使用Ingraham等人（2019）策划的CATH 4.2数据集，其中所有非重复性为40%的可用结构都按照其CATH（类别、架构、拓扑/折叠、同源超家族）分类进行划分。训练、验证和测试拆分分别由18204、608和1120个结构组成。
作者还报告了TS50的结果，这是一个由50个原生结构组成的较旧测试集，由Li等人（2014）首次引入。该基准的较小尺寸还允许与Rosetta中基于物理的计算昂贵的fixbb协议计算进行比较，Rosetta是一个在结构生物学界建立良好的软件套件。TS50不存在规范的训练和验证集。为了评估TS50，作者对CATH 4.2训练和验证集进行筛选，筛选出与TS50中任何序列的相似性小于30%（由PSIBLAST计算）的序列。
模型质量评估：模型质量评估（MQA）旨在从大量候选结构中选择蛋白质的最佳结构模型。在社区范围的结构预测关键评估（CASP）中，每两年评估一次不同MQA方法的性能。对于许多最近解决但尚未发布的结构（称为目标），结构生成程序会生成大量候选结构。MQA方法通过预测候选结构的GDT-TS分数与该目标的实验求解结构的比较来评估。GDT-TS是衡量两个蛋白质主干在全局对齐后的相似程度的标量指标。
除了准确预测候选结构的绝对质量外，好的MQA方法还应能够准确评估给定目标候选库中的相对模型质量，以便选择最佳模型，或许是为了进一步完善。因此，MQA方法通常基于两个指标进行评估：所有目标的预测和ground truth分数之间的全局相关性，以及仅特定目标候选结构之间的平均目标相关性。作者在实验中遵循这个惯例。
作者对提交给CASP 5-10的528个目标的79200个候选结构进行了训练和验证。然后，在两个MQA数据集上测试GVP-GNN。首先，对来自CASP 11（84个目标）和12（40个目标）的20880个第一阶段和第二阶段候选结构进行评分。该基准由Karasikov等人（2019年）首次建立，并被许多最近发布的方法所使用。其次，为了与更多关于近期结构数据的方法进行比较，作者还对来自CASP 13的1472个第2阶段候选结构（20个目标）进行了评分。作者将CASP 11-12结构添加到他们的训练集中，以评估CASP 13。有关MQA数据集的更多详细信息，请参见附录C。

五、实验

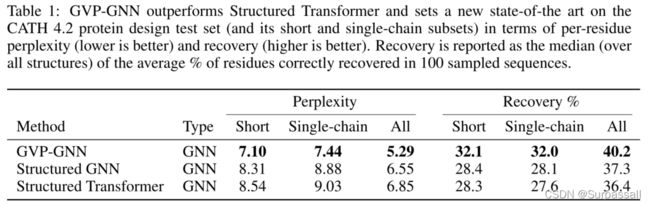
蛋白质设计：GVP-GNN在CATH 4.2上实现了最先进的性能，在复杂度和序列恢复方面都比Structured Transformer有了实质性的改进，Structured Transformer是一种GNN方法，作者使用和它相同的训练和验证集进行训练（表1）。继Ingraham等人（2019年）之后，作者报告了对CATH 4.2测试集的短（100个或更少的氨基酸残基）和单链亚群的评估，除完整测试集外，该测试集分别包含94个和103个蛋白质。尽管Structured Transformer在蛋白质的图结构化表示上利用了注意机制，但Structured Transformer的作者在消融研究中指出，消除注意似乎可以提高性能。因此，本文作者对Structured Transformer的一个版本进行了再训练，并将其与标准图传播操作（Structured GNN）替换了注意层的版本进行了比较。作者的方法也改进了这个模型。

在较小的测试集TS50上，与Rosetta的30%相比，作者实现了44.9%的恢复率，并且优于基于三类结构表示的方法。总体而言，作者在9种方法中的恢复率排名第二（见附录E）。然而，考虑到不同的方法没有使用规范化的训练数据集，这个测试集的结果应该是有保留的。
模型质量评估：在表2中的CASP 11-12测试集上，作者将GVP-GNN与其他单一结构、仅结构的方法进行了比较。其中包括CNN方法3DCNN（Derevyanko等人，2018年）和Ornate（Pagès等人，2019年）、GNN方法GraphQA（Baldas sarre等人，2020年）以及三种使用序列表示法VoroMQA（Olechnoviˍc&V enclovas，2017年）、SBROD（Karasikov等人，2019年）和ProQ3D（Uzilla等人，2017年）的方法。所有这些方法都只从蛋白质结构中学习，ProQ3D除外，它还使用基于比对的序列图谱。作者加入ProQ3D是因为它是CASP 11和CASP 12中最佳单模型方法的改进版本（Uziela等人，2017）。GVP-GNN在全局相关性和每目标相关性方面都优于所有其他结构化方法，甚至在除一个基准外的所有基准上都优于ProQ3D。作者还训练和评估了DimeNet，这是一种最新的3D感知GNN架构，在CASP 11-12上实现了许多小分子任务的最新技术（Klicpera等人，2019）。DimeNet的表现并不优于表2中的任何模型（见附录E）。

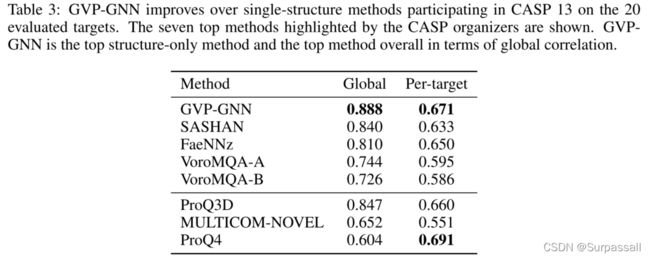
作者将GVP-GNN与参与CASP 13的所有23种单结构MQA方法进行了比较，可以对20个评估目标进行完整预测。Cheng等人（2019年）的CASP组织者强调了其中七种方法的最佳表现，并将其与GVP-GNN一起显示在表3中。其中包括四种仅从结构特征学习的方法和三种也使用序列轮廓的方法。SASHAN学习二级结构和接触特征的线性模型（Cheng等人，2019年）。FaeNNz8（Studer等人，2020年）、ProQ3D（Uziela等人，2017年）和VoroMQA9（Olechnoviˇc&V enclovas，2017年）在这些结构特征的基础上学习多层感知机或统计潜力。最后，MULTICOM-NOVEL（Hou等人，2019年）和ProQ4（Hurtado等人，2018年）在序列表示的基础上采用了一维深卷积网络。GVP-GNN在全局相关性方面优于所有方法，在单目标相关性方面优于所有纯结构方法。完整结果见附录E。

最后，由于作者的模型架构在每个节点嵌入时都会更新向量特征和标量特征，因此可以在经过训练的MQA网络的中间层中可视化学习到的向量特征。作者在附录F中展示并讨论了这些特征的可解释性。
消融实验：作者比较过的方法包括许多GNN（Structured Transformer/GNN、ProteinVersion、GraphQA）。作者为CPD和MQA训练了许多消融模型，以确定GVP中最有助于改善这些GNN性能的方面（表4）。将GVP替换为普通的MLP层或仅传播标量特征都会消除对几何信息的直接访问，迫使模型学习几何的标量值间接表示。这些修改导致性能大幅下降，突出了直接访问几何信息的重要性。仅传播向量特征会导致更大的减少，因为它既消除了重要的标量输入特征（如扭转角和氨基酸身份），也消除了GVP中具有近似保证的部分。因此，GVP的双标量/向量设计至关重要：如果没有这两种设计，最好的消融模型在CPD上就达不到Structured GNN，只能与MQA上的GraphQA相匹配。最后，消除第二个向量量变换 ${\mathbf{W}}_{\mu }$ 会导致性能略有下降。因此，所有架构元素都有助于对最先进技术的改进。

六、结论

在这项工作中，作者开发了第一个专门用于学习三维大分子结构的双重关系和几何表示的体系结构GVP-GNN。GVP-GNN的核心是用计算简单的层来扩充图神经网络，这些层对欧几里得向量特征执行表达性几何推理。作者的方法具有理想的理论性质，在从蛋白质结构学习质量分数和序列设计方面，经验上优于现有的体系结构。
GVP层在3D平移和旋转方面的等变性也突显了与利用$SO(3)$的不可约表示来定义点云上等变卷积的方法的相似性（Thomas等人，2018；Anderson等人，2019）。这些方法允许高阶张量的等变表示，但由于其复杂性和计算成本，其应用直到最近才限于小分子（Eismann等人，2020）。作者的体系结构提供了一种替代的、相对轻量级的等变方法，非常适合于大生物分子和生物分子复合物。
在进一步的工作中，作者希望将他们的体系结构应用到其他重要的结构生物学问题领域，包括蛋白质复合物、RNA结构和蛋白质-配体相互作用。