最近邻插值与双线性插值

最近邻插值

顾名思义，最近邻插值法在放大图像时补充的像素是最近邻的像素的值。由于方法简单，所以处理速度很快，但是得到的图像常常含有锯齿边缘。如下图所示：

import cv2
import numpy as np
def function(img):
    height,width,channels =img.shape
    emptyImage=np.zeros((800,800,channels),np.uint8)
    sh=800/height
    sw=800/width
    for i in range(800):
        for j in range(800):
            x=int(i/sh)
            y=int(j/sw)
            emptyImage[i,j]=img[x,y]
    return emptyImage

img=cv2.imread("path/lenna.png")
zoom=function(img)
print(img.shape)
print(zoom.shape)
cv2.imshow("image",img).              #(512,512,3)
cv2.imshow("nearest interp",zoom)     #(800,800,3)
cv2.waitKey(0)

双线性插值

先说说简单的单线性插值函数

根据P1和P2两个点可以确定直线方程为：

整理后：

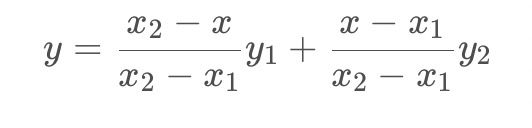
也就能得出P点的y值。
双线性插值也就是要在两个方向进行插值。

假设我们已知函数 f 在 Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1) 以及 Q22 = (x2, y2) 四个点的值，想得到未知函数 f 在点 P = (x, y) 的值，首先在 x 方向进行线性插值，得到：


然后在y方向进行线性插值，得到：

整合后的公式如下：

在实际代码中，还会将源图像和目标图像进行中心对齐，如下图，假设你需要将一幅5x5的图像缩小成3x3，那么源图像和目标图像各个像素之间的对应关系如下。如果没有这个中心对齐，就会得到左边的结果，图像的像素信息会丢失；而用了对齐，就会得到右边的结果：

import numpy as np
import cv2
def bilinear_interpolation(img,out_dim):
    src_h, src_w, channel = img.shape
    dst_h, dst_w = out_dim[1], out_dim[0]
    print ("src_h, src_w = ", src_h, src_w)
    print ("dst_h, dst_w = ", dst_h, dst_w)
    if src_h == dst_h and src_w == dst_w:
        return img.copy()
    dst_img = np.zeros((dst_h,dst_w,3),dtype=np.uint8)
    scale_x, scale_y = float(src_w) / dst_w, float(src_h) / dst_h
    for i in range(3):
        for dst_y in range(dst_h):
            for dst_x in range(dst_w):
                #中心对齐
                src_x = (dst_x + 0.5) * scale_x - 0.5
                src_y = (dst_y + 0.5) * scale_y - 0.5
                #找到插值用的坐标点
                src_x0 = int(np.floor(src_x))
                src_x1 = min(src_x0 + 1 ,src_w - 1)
                src_y0 = int(np.floor(src_y))
                src_y1 = min(src_y0 + 1, src_h - 1)
                #代入计算
                temp0 = (src_x1 - src_x) * img[src_y0,src_x0,i] + (src_x - src_x0) * img[src_y0,src_x1,i]
                temp1 = (src_x1 - src_x) * img[src_y1,src_x0,i] + (src_x - src_x0) * img[src_y1,src_x1,i]
                dst_img[dst_y,dst_x,i] = int((src_y1 - src_y) * temp0 + (src_y - src_y0) * temp1)
 
    return dst_img
 
if __name__ == '__main__':
    img = cv2.imread('path/lenna.png')
    dst = bilinear_interpolation(img,(700,700))
    cv2.imshow('bilinear interp',dst)
    cv2.waitKey()

这种方式得到的图像就不会出现锯齿现象。