强化学习中的multiarmed-Bandit以及经典解法epsilon-greedy算法与UCB算法，附加python实现

最近在看Management Science上的文章《A Dynamic Clustering Approach to Data-Driven Assortment Personalization》，其中提到了一个Multiarmed-Bandit模型，想要深入学习一下，但是查遍各种网站，都没有中文的关于这个问题的介绍，因此去油管上学习，然后翻译成中文在这里跟大家分享。

Exploration and exploitation tradeoff

在强化学习中有一个经典问题，即Exploration and esploitation tradeoff，在该问题中有一个两难境地：到底我们应该花精力去探索从而对收益有更精确的估计，还是应该按照目前拥有的信息，选择最大收益期望的行动？
由此引申出Multiarmed-Bandit模型

Multiarmed-Bandit Model

假设现在有n台老虎机，每台老虎机的收益不同，但我们事先并不知道每台老虎机的期望收益。
我们在这里假设：每台老虎机的收益服从方差为1的正态分布，均值事先并不知道。我们需要探索每台老虎机的收益分布，并最终让行动选择拥有最有的期望收益的老虎机。

传统的解决方案 A/B test

A/B test的思路是，给每台老虎机分配数量相同的测试数目，然后根据所有老虎机的测试结果，选择表现最优的老虎机进行剩下的所有操作。
这种方法的最大劣势就是将探索与开发割裂开来。在探索过程中只考虑探索，只收集信息，而在开发的阶段就不再考虑探索，也就失去了学习的机会，有可能陷入了局部最优，没有找到最优的老虎机。

epsilon-greedy 算法

epsilon-greedy算法也是一种贪婪算法，不过在每次选择的过程中，会以一个较小的改了选择不是最优行动的其他行动，从而能够不断进行探索。由于epsilon较少，并且最终算法会找到最优的行动，因此最终选择最优的行动的概率会趋近于1-epsilon。
下面展示python代码：

import numpy as np
import matplotlib.pyplot as plt


class EpsilonGreedy:
    def __init__(self):
        self.epsilon = 0.1  # 设定epsilon值
        self.num_arm = 10  # 设置arm的数量
        self.arms = np.random.uniform(0, 1, self.num_arm)  # 设置每一个arm的均值，为0-1之间的随机数
        self.best = np.argmax(self.arms)  # 找到最优arm的index
        self.T = 50000  # 设置进行行动的次数
        self.hit = np.zeros(self.T)  # 用来记录每次行动是否找到最优arm
        self.reward = np.zeros(self.num_arm)  # 用来记录每次行动后各个arm的平均收益
        self.num = np.zeros(self.num_arm)  # 用来记录每次行动后各个arm被拉动的总次数

    def get_reward(self, i):  # i为arm的index
        return self.arms[i] + np.random.normal(0, 1)  # 生成的收益为arm的均值加上一个波动

    def update(self, i):
        self.num[i] += 1
        self.reward[i] = (self.reward[i]*(self.num[i]-1)+self.get_reward(i))/self.num[i]

    def calculate(self):
        for i in range(self.T):
            if np.random.random() > self.epsilon:
                index = np.argmax(self.reward)
            else:
                a = np.argmax(self.reward)
                index = a
                while index == a:
                    index = np.random.randint(0, self.num_arm)
            if index == self.best:
                self.hit[i] = 1  # 如果拿到的arm是最优的arm，则将其记为1
            self.update(index)

    def plot(self):  # 画图查看收敛性
        x = np.array(range(self.T))
        y1 = np.zeros(self.T)
        t = 0
        for i in range(self.T):
            t += self.hit[i]
            y1[i] = t/(i+1)
        y2 = np.ones(self.T)*(1-self.epsilon)
        plt.plot(x, y1)
        plt.plot(x, y2)
        plt.show()


E = EpsilonGreedy()
E.calculate()
E.plot()

最终的结果如下图所示：

随着行动的不断进行，累计准确率（选到最优arm的频率）在不断上升，并且逼近了我们所设置的上线$1-ϵ$，证明了$ϵ$-greedy算法的有效性！

UCB算法

在解决multiarmed-bandit问题中，还有一个比$ϵ$-greedy算法更加实用的算法，称为Upper Confidence Bound(UCB)算法。
在$ϵ$-greedy算法收敛后，始终会以一个$ϵ$的概率去选择不是最优的方案，而此时最优的方案大概率已经被找到，因此就造成了白白的浪费。UCB算法就很好的解决了这个问题。
下面展示UBC的python代码：

import numpy as np
import matplotlib.pyplot as plt


# Set δ = 1/n**4 in Hoeffding's bound
# Choose a with highest Heoffding bound

class UCB:
    def __init__(self):
        self.num_arm = 10  # 设置arm的数量
        self.arms = np.random.uniform(0, 1, self.num_arm)  # 设置每一个arm的均值，为0-1之间的随机数
        self.best = np.argmax(self.arms)  # 找到最优arm的index
        self.T = 100000  # 设置进行行动的次数
        self.hit = np.zeros(self.T)  # 用来记录每次行动是否找到最优arm
        self.reward = np.zeros(self.num_arm)  # 用来记录每次行动后各个arm的平均收益
        self.num = np.ones(self.num_arm)*0.00001  # 用来记录每次行动后各个arm被拉动的总次数
        self.V = 0
        self.up_bound = np.zeros(self.num_arm)

    def get_reward(self, i):  # i为arm的index
        return self.arms[i] + np.random.normal(0, 1)  # 生成的收益为arm的均值加上一个波动

    def update(self, i):
        self.num[i] += 1
        self.reward[i] = (self.reward[i]*(self.num[i]-1)+self.get_reward(i))/self.num[i]
        self.V += self.get_reward(i)

    def calculate(self):
        for i in range(self.T):
            for j in range(self.num_arm):
                self.up_bound[j] = self.reward[j] + np.sqrt(2*np.log(i+1)/self.num[j])
            index = np.argmax(self.up_bound)
            if index == self.best:
                self.hit[i] = 1
            self.update(index)

    def plot(self):  # 画图查看收敛性
        x = np.array(range(self.T))
        y1 = np.zeros(self.T)
        t = 0
        for i in range(self.T):
            t += self.hit[i]
            y1[i] = t/(i+1)
        plt.plot(x, y1)
        plt.show()


U = UCB()
U.calculate()
U.plot()

运行之后的结果为：

可见，随着行动不断进行，累计选取最优老虎机的频率不断上升，并且没有1-$ϵ$上限。

$ϵ$-greedy算法与UCB算法对比

为了更好说明UCB算法的优越性，我们将这两种算法放在一起进行对比，代码如下：

import numpy as np
import matplotlib.pyplot as plt


class MultiArmedBandit:
    def __init__(self):
        self.epsilon = 0.1  # 设定epsilon值
        self.num_arm = 10  # 设置arm的数量
        self.arms = np.random.uniform(0, 1, self.num_arm)  # 设置每一个arm的均值，为0-1之间的随机数
        self.best = np.argmax(self.arms)  # 找到最优arm的index
        self.T = 100000  # 设置进行行动的次数
        self.hit_epsilon = np.zeros(self.T)  # 用来记录每次行动是否找到最优arm
        self.hit_ucb = np.zeros(self.T)
        self.reward_epsilon = np.zeros(self.num_arm)  # 用来记录每次行动后各个arm的平均收益
        self.reward_ucb = np.zeros(self.num_arm)
        self.num_epsilon = np.zeros(self.num_arm)  # 用来记录每次行动后各个arm被拉动的总次数
        self.num_ucb = np.ones(self.num_arm)*0.000000001
        self.V_epsilon = 0
        self.V_ucb = 0
        self.up_bound = np.zeros(self.num_arm)

    def get_reward(self, i):  # i为arm的index
        return self.arms[i] + np.random.normal(0, 1)  # 生成的收益为arm的均值加上一个波动

    def update_epsilon(self, i):
        self.num_epsilon[i] += 1
        self.reward_epsilon[i] = (self.reward_epsilon[i]*(self.num_epsilon[i]-1)+self.get_reward(i))/self.num_epsilon[i]
        self.V_epsilon += self.get_reward(i)

    def update_ucb(self, i):
        self.num_ucb[i] += 1
        self.reward_ucb[i] = (self.reward_ucb[i]*(self.num_ucb[i]-1)+self.get_reward(i))/self.num_ucb[i]
        self.V_ucb += self.get_reward(i)

    def calculate_epsilon(self):
        for i in range(self.T):
            if np.random.random() > self.epsilon:
                index = np.argmax(self.reward_epsilon)
            else:
                a = np.argmax(self.reward_epsilon)
                index = a
                while index == a:
                    index = np.random.randint(0, self.num_arm)
            if index == self.best:
                self.hit_epsilon[i] = 1  # 如果拿到的arm是最优的arm，则将其记为1
            self.update_epsilon(index)

    def calculate_ucb(self):
        for i in range(self.T):
            for j in range(self.num_arm):
                self.up_bound[j] = self.reward_ucb[j] + np.sqrt(2*np.log(i+1)/self.num_ucb[j])
            index = np.argmax(self.up_bound)
            if index == self.best:
                self.hit_ucb[i] = 1
            self.update_ucb(index)

    def plot_epsilon(self):  # 画图查看收敛性
        x = np.array(range(self.T))
        y1 = np.zeros(self.T)
        y3 = np.zeros(self.T)
        t = 0
        for i in range(self.T):
            t += self.hit_epsilon[i]
            y1[i] = t/(i+1)
        t = 0
        for i in range(self.T):
            t += self.hit_ucb[i]
            y3[i] = t/(i+1)
        y2 = np.ones(self.T)*(1-self.epsilon)
        plt.plot(x, y1, label='epsilon-greedy')
        plt.plot(x, y2, label='1-epsilon')
        plt.plot(x, y3, label='UCB')
        plt.legend(loc='right', prop={'size': 18})
        plt.show()


E = MultiArmedBandit()
E.calculate_epsilon()
E.calculate_ucb()
print(E.V_ucb)
print(E.V_epsilon)
E.plot_epsilon()

采用相同的老虎机，我们看最终那种算法的效果与累计收益更好。
代码的运行结果如下：
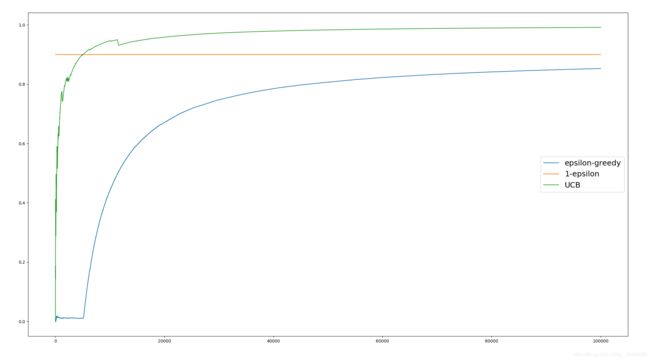可见，UCB方法明显优于$ϵ$-greedy算法，能够突破$1-ϵ$的界限。最终的累计收入如下图：

UCB的累计收入也要高于$ϵ$-greedy算法。