利用GCN图卷积神经网络求解数独问题

利用GCN图卷积神经网络求解数独问题

前言

数独（shù dú, Sudoku）是源自18世纪瑞士的一种数学游戏。是一种运用纸、笔进行演算的逻辑游戏。玩家需要根据9×9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫（3*3）内的数字均含1-9，不重复。

数独盘面是个九宫，每一宫又分为九个小格。在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字。使1-9每个数字在每一行、每一列和每一宫中都只出现一次，所以又称“九宫格”。

---

是否能利用深度学习进行数独问题的求解，有不少学者也已经进行过这方面的探索Rasmus Berg Palm和等人构造了相应的RRN(Recurrent Relationlation Network)网络结构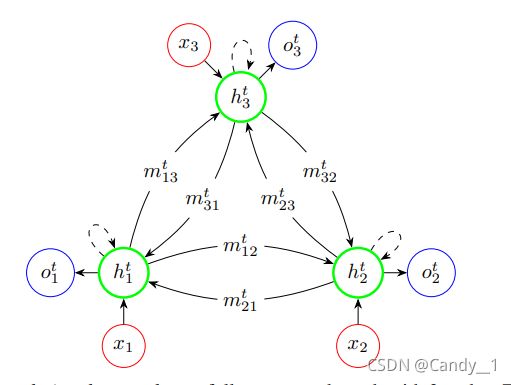
。该结构采用信息传递机制，定义9×9数独的每一个元胞为一个节点，满足数独规则的同一行，同一列或者同一个块为相邻节点，这样就定义了节点的相邻关系以及信息在节点之间的流动：
$$m_{ij}^t=f(h_i^{t-1},h_j^{t-1})$$

$m_{ij}$为$t$时刻从$i$节点到j节点传递的信息，$h_i^{t-1}$为$t-1$时刻$i$节点的隐藏状态。
有了相邻节点传递的信息之后就可以表示某一结点拥有的节点信息：
$$m_j^t=\sum _{i\in N(i)}{m}_{ij}^t$$将节点信息嵌入到网络中便是RRN网络的精髓。

---

Park等人也尝试过CNN直接解决数独问题，建立10层卷积层[512]将数独问题暴力求解，也得到了很好的效果。

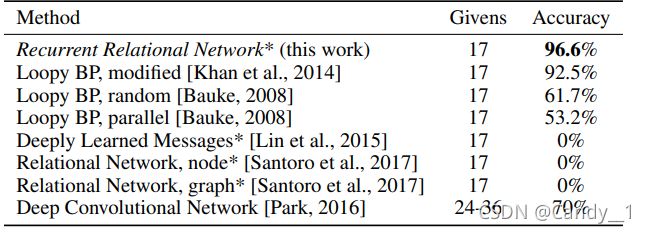
本篇主要依托GCN及其CNN去尝试解决数独问题。所基于的深度学习框架为tensorflow2.7.

数据准备

这个数据集包含了1百万数独的数据，你可以在这里找到它。https://www.kaggle.com/bryanpark/sudoku

• 点击Download下载164M的CSV数独数据文件并解压至目录。

#构建数组数据
import numpy as np
quizzes = np.zeros((1000000, 81), np.int32)
solutions = np.zeros((1000000, 81), np.int32)
for i, line in enumerate(open('sudoku.csv', 'r').read().splitlines()[1:]):
    quiz, solution = line.split(",")
    for j, q_s in enumerate(zip(quiz, solution)):
        q, s = q_s
        quizzes[i, j] = q
        solutions[i, j] = s
quizzes = quizzes.reshape((1000000, 9, 9,1))/10
solutions = solutions.reshape((1000000,9,9))

这里得到了1000000个数独数据的问题和解答，可以这样查看：

#数据尺寸
quizzes[2].reshape((9,9))*10

同样查看数独解答：

solutions[2].reshape((9,9))

数据已构建完毕。接下来由于tensorflow用到了一些老版本的运行机制，首先先把模式转化成eager模式。

from tensorflow.python.framework.ops import disable_eager_execution
disable_eager_execution()

下面便是网络的构建部分。

网络构建

GCN

1.构造图

说到GCN，可以试着回顾一下GCN的机制。
GCN，图卷积神经网络，实际上跟CNN的作用一样，就是一个特征提取器，只不过它的对象是图数据。GCN精妙地设计了一种从图数据中提取特征的方法，从而让我们可以使用这些特征去对图数据进行节点分类（node classification）、图分类（graph classification）、边预测（link prediction），还可以顺便得到图的嵌入表示（graph embedding），可见用途广泛。因此现在人们脑洞大开，让GCN到各个领域中发光发热。

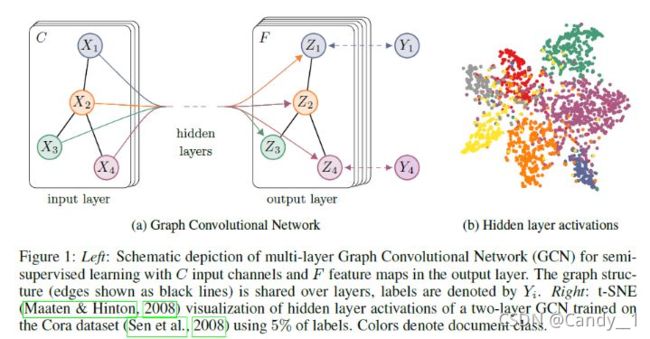
其核心公式为：

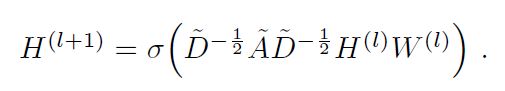
• A波浪=A+I，I是单位矩阵

• D波浪是A波浪的度矩阵（degree matrix）

• H是每一层的特征，对于输入层的话，H就是X

• σ是非线性激活函数

回到我们的数独问题，假如我们把原数独9×9的每一个元胞看作是一个节点的话，一个数独就包括了81个节点。考虑到规则为每一行、每一列、每一个粗线宫（3*3）内的数字均含1-9，不重复。 我们借鉴RRN思路，将每一行、每一列、每一个粗线宫的节点设置为相邻节点(即所谓的邻居).我们将所有的节点编号，相邻节点用颜色标出，如下图所示：

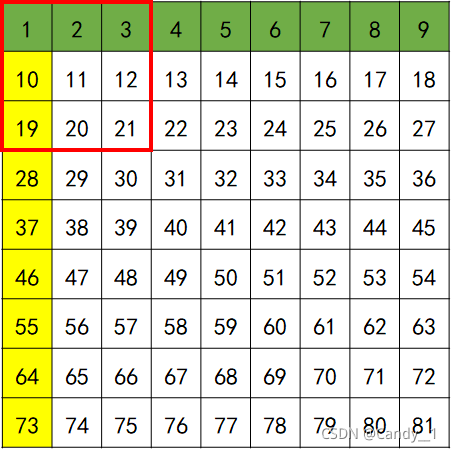
以1节点为例，黄色部分为同一列的相邻节点，绿色部分为同一行的相邻节点，红色框线部分为同一宫格内的相邻节点。遍历所有节点，把上述关系绘制成如下：

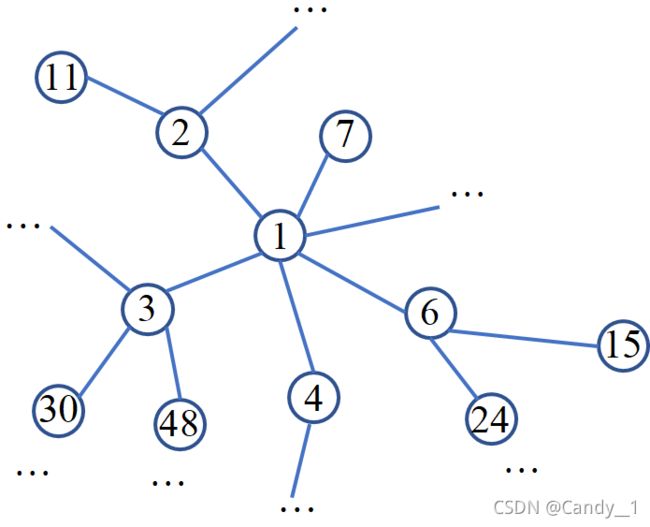
便可构成一副无向图。注意本次图构造并未区分不同邻居(行邻居、列邻居、宫邻居）也就是将图的 所有边权重设置为相同，后续读者对这个感兴趣可以自行尝试。
有了这副图之后便可构造邻接矩阵及其度矩阵。
这里只是举了一个例子 ：

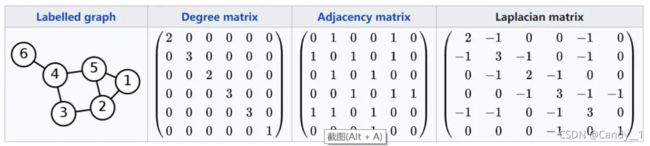
下面便是核心代码：

import tensorflow as tf
#构造数独图及其邻接矩阵A
def sudoku_edges():
        def cross(a):
            return [(i, j) for i in a.flatten() for j in a.flatten() if not i == j]

        idx = np.arange(81).reshape(9, 9)
        rows, columns, squares = [], [], []
        for i in range(9):
            rows += cross(idx[i, :])
            columns += cross(idx[:, i])
        
        for i in range(3):
            for j in range(3):
                squares += cross(idx[i * 3:(i + 1) * 3, j * 3:(j + 1) * 3])
        self_link = [(i, i) for i in range(81)]
        edges=list(set(rows + columns + squares))
       
        A = np.zeros((81, 81))
        for i, j in edges:
            A[j, i] = 1
            A[i, j] = 1

        return A
#归一化邻接矩阵
def normalize_digraph(A):
    Dl = np.sum(A, 0)
    num_node = A.shape[0]
    Dn = np.zeros((num_node, num_node))
    for i in range(num_node):
        if Dl[i] > 0:
            Dn[i, i] = Dl[i]**(-1)
    AD = np.dot(A, Dn)
    return AD
#设置边界权重：所有权重相等
A=sudoku_edges()*np.ones((81,81))
print(A)
AD=normalize_digraph(A)
AD=AD.reshape(1,81,81)
print(AD)
A=tf.convert_to_tensor(AD)#(1,81,81)
A=tf.cast(A,dtype=tf.float32)

2.搭建网路

#网络搭建
input_shape=(1000,9,9,1)

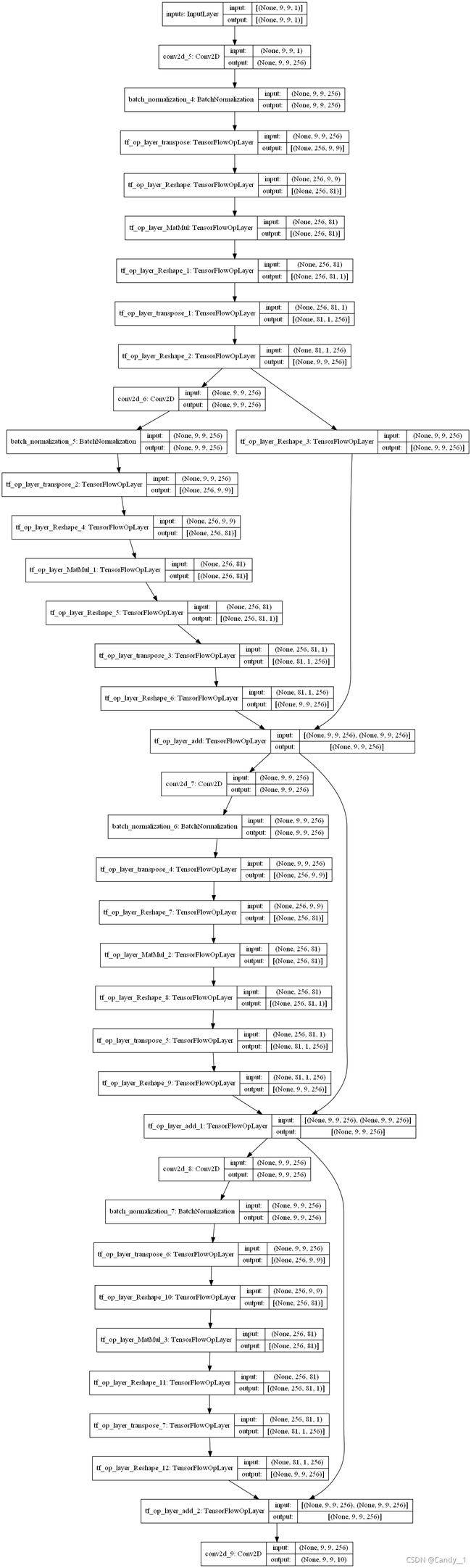
def GCNNet(inputs):
    """ 
   定义网络结构
采用4层网络，参考Kyubyong/sudoku,每一层采用Res机制防止梯度消失，每一层采用批归一化获得稳定输出

输入：
    inputs:[N,9,9.1]的样本
    outputs:[N,9,9,10]的logit

   """

    
   
    conv1=tf.keras.layers.Conv2D(256, (3,3),activation='relu',padding='same', input_shape=input_shape[1:])(inputs)#(N,9,9,64)
    conv1=tf.keras.layers.BatchNormalization()( conv1)
    conv1=tf.transpose(conv1,perm=[0,3,1,2])#(N,64,9,9)
    conv1=tf.reshape(conv1,[-1,256,9*9])#(N,64,81)
    conv1=tf.matmul(conv1,A)#(N,64,81)
    conv1=tf.reshape(conv1,[-1,256,81,1])
    conv1=tf.transpose(conv1,perm=[0,2,3,1])#(N,81,1,64)
    conv1=tf.reshape(conv1,[-1,9,9,256])
    res1=tf.reshape(conv1,[-1,9,9,256])
    
    conv1=tf.keras.layers.Conv2D(256, (3,3),activation='relu',padding='same')(conv1)
    conv1=tf.keras.layers.BatchNormalization()( conv1)
    conv1=tf.transpose(conv1,perm=[0,3,1,2])#(N,64,9,9)
    conv1=tf.reshape(conv1,[-1,256,9*9])#(N,64,81)
    conv1=tf.matmul(conv1,A)#(N,64,81)
    conv1=tf.reshape(conv1,[-1,256,81,1])
    conv1=tf.transpose(conv1,perm=[0,2,3,1])#(N,81,1,64)
    conv1=tf.reshape(conv1,[-1,9,9,256])
    conv1=conv1+res1
    res2=conv1
    conv1=tf.keras.layers.Conv2D(256, (3,3),activation='relu',padding='same')(conv1)
    conv1=tf.keras.layers.BatchNormalization()( conv1)
    conv1=tf.transpose(conv1,perm=[0,3,1,2])#(N,64,9,9)
    conv1=tf.reshape(conv1,[-1,256,9*9])#(N,64,81)
    conv1=tf.matmul(conv1,A)#(N,64,81)
    conv1=tf.reshape(conv1,[-1,256,81,1])
    conv1=tf.transpose(conv1,perm=[0,2,3,1])#(N,81,1,64)
    conv1=tf.reshape(conv1,[-1,9,9,256])
    conv1=res2+conv1
    res3=conv1
    
    conv1=tf.keras.layers.Conv2D(256, (3,3),activation='relu',padding='same')(conv1)
    conv1=tf.keras.layers.BatchNormalization()( conv1)
    conv1=tf.transpose(conv1,perm=[0,3,1,2])#(N,64,9,9)
    conv1=tf.reshape(conv1,[-1,256,9*9])#(N,64,81)
    conv1=tf.matmul(conv1,A)#(N,64,81)
    conv1=tf.reshape(conv1,[-1,256,81,1])
    conv1=tf.transpose(conv1,perm=[0,2,3,1])#(N,81,1,64)
    conv1=tf.reshape(conv1,[-1,9,9,256])
    conv1=res3+conv1

    outputs0=tf.keras.layers.Conv2D(10, (3,3),activation='softmax',padding='same')( conv1)

    print(outputs0.shape)
    return outputs0

inputs = tf.keras.layers.Input(shape=(9,9,1), name='inputs')
outputs0=GCNNet(inputs)
auto_encoder =tf.keras.Model(inputs,outputs0)
auto_encoder.summary()

总共参数为1799946个

3.自定义损失函数

这里采用稀疏交叉熵，并传入目标参数便能直接在数独空缺部分直接计算损失。

class WeightedSDRLoss(tf.keras.losses.Loss):
    

    def __init__(self, noisy_signal, reduction=tf.keras.losses.Reduction.AUTO, name='WeightedSDRLoss'):
        super().__init__(reduction=reduction, name=name)
        self.x = x=tf.squeeze(noisy_signal)
        self.istarget=tf.compat.v1.to_float(tf.equal(self.x,tf.zeros_like(self.x)))

        

    def call(self, y_true, y_pred):
        loss=tf.keras.metrics.sparse_categorical_crossentropy(y_true,y_pred)#（None，9，9）
        print("the shape of loss is{}".format(loss.shape))
        print("the shape of istarget is{}".format(self.istarget.shape))
        return tf.reduce_sum(loss*self.istarget)/(tf.reduce_sum(self.istarget))

4.模型编译

auto_encoder.compile(optimizer='adam', loss=WeightedSDRLoss(inputs))

5.模型训练

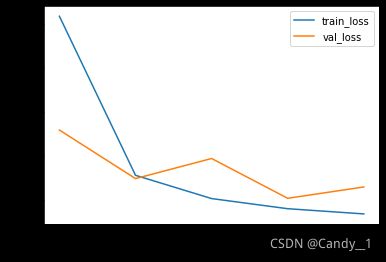
history = auto_encoder.fit(quizzes, solutions, batch_size=128, shuffle=True,epochs=5,validation_split=0.3)

训练5轮之后，损失图如下：

6.模型预测与评估

由于最后输出层采用softmax激活获得每一像素的概率，预测并非一次性将所有空格填补出来，而是启发式地依次迭代填补空格：

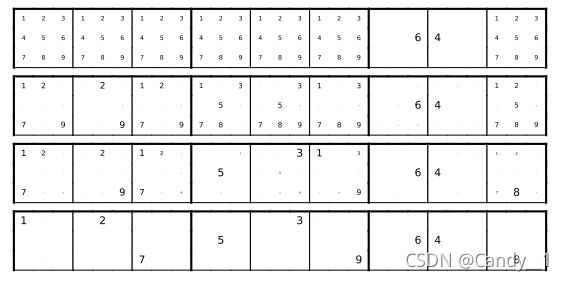
#进行预测，这里选第1个数独进行预测：
n=10#数独1
x=quizzes[n]
y=solutions[n].reshape(1,9,9)
x_=x.reshape(1,9,9)

x__=x.reshape(1,9,9,1)

temp=[]
for i in range(80):
    #print("第{}轮".format(i))
    pred_=tt.predict(x.reshape(1,9,9,1))
   
    istarget=(np.equal(x__,np.zeros_like(x__))).astype(np.float64)
    pred_= pred_* istarget
    
    prob=np.max(pred_, axis=-1) #(N,9,9)
    #prob=prob* istarget
    prob=prob.reshape(1,81)
    prob[:,temp]=0
    pred=np.argmax(pred_,axis=-1)
    #pred=pred*istarget
    pred=pred.reshape(1,81)
    maxprob_ids=np.argmax(prob,axis=1)
    temp.append( maxprob_ids)
    print(prob)
    #print('-----------------')
    x=np.reshape(x,(1,81))
   
    x[:,maxprob_ids]=pred[:,maxprob_ids]/10
    print("将{}位置处的变成{}".format(maxprob_ids,pred[:,maxprob_ids]/10))
    prob[:,maxprob_ids]
    x=np.reshape(x,(1,9,9))
   
    
    
    x=np.where(x_==0,x,y/10)
    #print("还剩下{}".format(x.size-np.count_nonzero(x)))
   
    if np.count_nonzero(x)==x.size:
       
        break
x=x.reshape(9,9) *10   
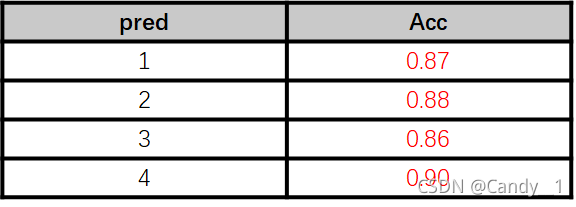
print("预测第{}个数独为:".format(n))
print(x)

这里选了5个数独进行测试：

便与比较，这里要设置了CNN网络结构：
采用10层网络，均为512输出通道：

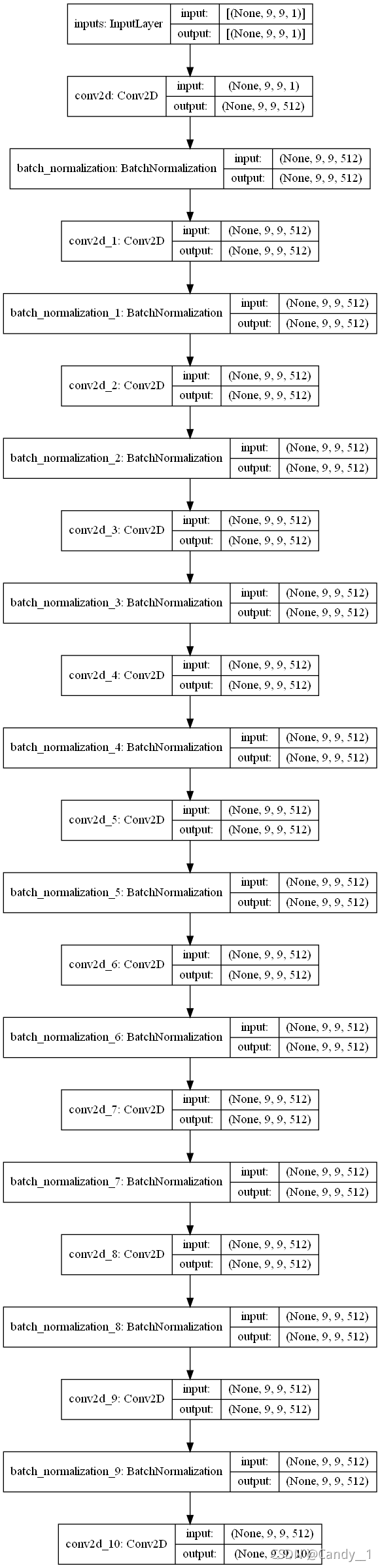
计算时长为GCN的7倍多，相应的损失函数也达到了较好的效果。

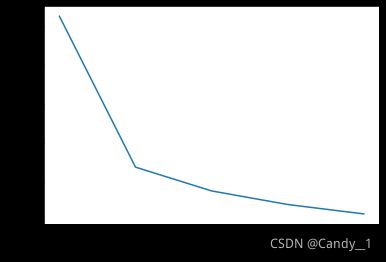
总结

设计GCN图神经网络解决数独难题，收敛较快并且有效提取了数独特征，较好地解决数独难题。读者可以自行对比采用CNN与GCN的效果，并自行更改网络结构。