图神经网络(二)GCN的性质(2)GCN能够对图数据进行端对端学习
图神经网络(二)GCN的性质(2)GCN能够对图数据进行端对端学习
近几年,随着深度学习的发展,端对端学习变得越来越重要,人们普遍认为,深度学习的成功离不开端对端学习的作用机制。端对端学习实现了一种自动化地从数据中进行高效学习的机制。然而,端对端学习的这种高度自动化的特性的达成,往往离不开背后大量的针对特定类型数据的学习任务的适配工作,,这种适配体现在当下十分流行的各种网络层或层块结构(block)的设计上,比如我们熟知的Conv2D层对于图像数据学习、LSTM层对于序列数据的学习、Global Pooling层对于全局信息的提取等。这些层的计算过程必须最大限度地按照我们期望的方式去适配数据的内在规律模式。大量的实践经验告诉我们,深度学习能够在某个场景任务中取得极其优秀的效果,很大程度上得益于这类网络层或者由该网络层所构建的网络层块的定制化设计[4]。
因此,如果我们要实现对于图数据的端对端学习,学习系统必须能够适配图数据的内在模式。
属性图是一种最广泛的图数据表现形式。在属性图里面,每个节点都有自己的属性。如图2-4中的a图所示,在某个社交网络的场景中,用户节点存在性别和年龄等属性,这些属性对用户身份的刻画是十分重要的。同时,我们可以看到图中有两个入度很高的节点,在很大程度上,这类节点表示的是社交网络里面的大V用户。图2-4中的b图所示为乙醇和甲醚的分子式和分子结构,虽然二者的分子式均为 C 2 H 6 O \text{C}_2 \text{H}_6 \text{O} C2H6O,但是由于分子结构不同,二者具有不同的理化性质。
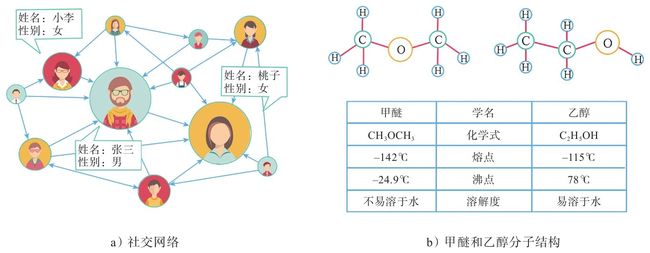 图2-4 图数据示例
图2-4 图数据示例
总结上面两个例子,我们可以发现,图数据中包含着两部分信息:属性信息与结构信息。属性信息描述了图中对象的固有性质;结构信息描述了对象之间的关联性质,这种由关联所产生的的结构不仅对图数据中节点的刻画具有很大的帮助作用,而且对该全图的刻画也起着关键作用。一个优秀的针对图数据的学习系统,必须能够做到对属性信息和结构信息进行端对端学习。
下面我们来看看GCN的设计是怎么去适配图数据的内在规律的。为了更形象地阐述GCN对于图数据的端对端学习能力,我们将之前提到的两类非常典型的图数据学习方式——基于手工特征与基于随机游走的方法进行对比。一般来说,图数据中枢性信息的处理是比较简单的,按照属性的类型进行相应的编码设计,然后将其拼接成一个表示节点属性的特征向量就可以了,但是结构信息蕴含在节点之间的关系中,是比较难处理的。我们所对比的两个方法的核心是在如何处理图的结构信息上,如图2-5、图2-6所示。
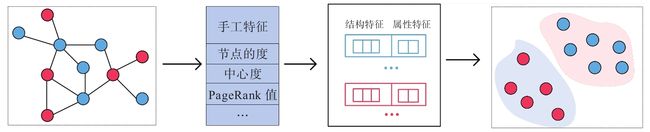 图2-5 基于手工特征的方法
图2-5 基于手工特征的方法
图2-5所示的方法是基于手工特征的方法,该方法对于图数据的处理方式非常依赖与人工干预,具体来说,就是将图中节点的结构信息以一些图的统计特征进行替代,常见的如节点的度、节点的中心度、节点的PageRank值等,然后将这个代表节点结构信息的特征向量与代表节点属性信息的特征向量拼接在一起,送到下游进行任务的学习。这种方法的最大问题在于,表示结构信息的特征向量需要人为定义,因此很难确定这些统计特征是否对学习后面的任务有效。
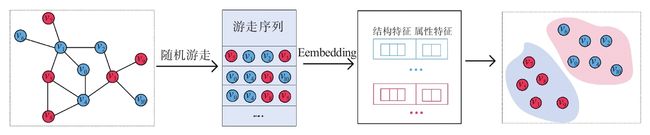 图2-6 基于随机游走的方法
图2-6 基于随机游走的方法
图2-6所示的方法是基于随机游走的方法,随机游走[1]是网络表示学习中最具代表性的方法之一,其基本思想是将图中节点所满足的关系与结构的性质映射到一个新的向量空间去,比如再图上距离更近的两个节点,在新的向量空间上的距离也更近。通过这样的优化目标将图里面的数据,转化成向量空间里面的数据,这样处理起来就会更加方便。接下来,该方法和基于手工特征的方法的思路一样,将代表节点结构信息的特征向量与代表节点属性信息的特征向量进行拼接,然后进行下游的任务学习。所不同的是,其节点的结构信息是通过随机游走类方法进行学习的,并不依赖认为定义,因此相比之下会更加高效。
图2-7是基于GCN的方法,从图中可以看到,GCN对于图数据的学习方式比较符合端对端的要求:一端是数据,另一端是任务。
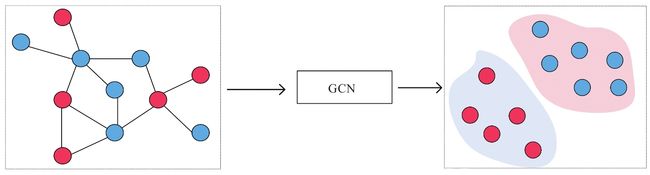 图2-7 基于GCN的方法
图2-7 基于GCN的方法
GCN对于属性信息和结构信息的学习体现在其核心计算公式上: L ~ sym X W \tilde{L}_\text{sym} XW L~symXW,这一计算过程可以被拆分成两步:
第1步: X W XW XW是对属性信息的仿射变换,学习了属性特征之间的交互模式;
第2步: L ~ sym ( X W ) \tilde{L}_\text{sym} (XW) L~sym(XW)从空域角度来看是聚合邻居节点的过程,代表了对节点局部结构信息的编码。
为了更进一步说明GCN对于图中的结构信息的学习能力,我们来看一个经典的图论问题——图的同构问题(graph isomorphism problem),即给定两个图,判断这两个图是否完全等价。
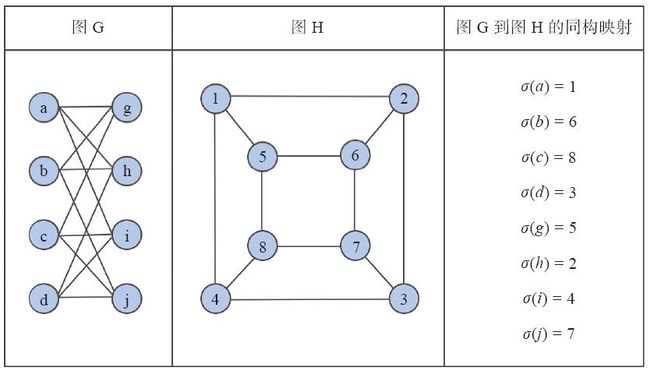 图2-8 图同构[1]
图2-8 图同构[1]
从图2-8中我们可以发现,即使看上去并不相似的两个图,也有可能是完全等价的。从同构图的定义中我们可以看到,要想解决这个问题,需要考量的是算法对图结构信息的分辨能力。一个经典的解法就是Weisfeiler-Lehman算法[2],Weisfeiler-Lehman算法是一个迭代式的算法,其算法流程如下所示:
对于图上任意一个节点 v i v_i vi:
1.获取邻居节点 v j ∈ N ( v i ) v_j∈N(v_i) vj∈N(vi)的标签 h j h_j hj;
2.更新 v i v_i vi的标签 h i ← hash ( ∑ v j h j ) h_i←\text{hash}(∑_{v_j}h_j ) hi←hash(∑vjhj),其中 hash ( ⋅ ) \text{hash}(\cdot) hash(⋅)是一个单射函数(一对一映射)。
我们可以看到,上述过程与节点层面的GCN计算过程基本一致:迭代式地聚合邻居节点的特征,从而更新当前节点的特征。从这个角度来看,GCN近似于一种带参的、支持自动微分的Weisfeiler-Lehman算法。在论文[3]中介绍了一种GCN的衍生模型——Graph Isomorphism Network(GCN),实验证明,其在判断图同构的问题上,能力近乎等价于Weisfeiler-Lehman算法。
在GCN模型中,通过堆叠图卷积层,上述属性信息的编码学习与结构信息的编码学习被不断地交替进行,如是完成对图数据中更加复杂的模式学习。GCN相较于上述两种方法,有如下两点优势:
(1)GCN对表示学习和任务学习一起进行端对端的优化,在前述两种方法中,节点的特征向量一旦被拼接起来就会被固化下来,下游任务学习中产生的监督信号并不能有效指导图数据的表示学习,这可能会使节点的特征表示对于下游的任务不是很高效的。相反,GCN对于图数据的建模并没有切分成两步来完成,对于节点的表示学习与下游的任务学习被放到一个模型里面进行端对端学习,整个模型的监督信号同时指导着任务层(如分类层)和GCN层的参数更新,节点的特征表示与下游任务之间具有更好的适应性。
(2)GCN对结构信息与属性信息的学习是同时进行的,并没有进行分拆和解构。通常来说,属性信息与结构信息具有很好地互补关系,对于一些结构稀疏的图来说,属性信息的补充可以很好地提高模型对节点表示学习的质量,另外,结构信息蕴含着属性信息中所没有的知识,对节点的刻画具有十分重要的作用。GCN将结构信息与属性信息放进一个网络层里面同时进行学习,使二者能够协同式地去影响最终节点的表示。
总的来说,GCN模型将学习过程直接架构与图数据智商,为图数据的学习提供了一套端对端的框架,对相关的任务学习具有更好的适应性。
参考文献
[1] Perozzi B, Al-Rfou R, Skiena S. Deepwalk: Online learning of social representations[C]//Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. 2014: 701-710.
[2] Weisfeiler B, Leman A. The reduction of a graph to canonical form and the algebra which appears therein[J]. NTI, Series, 1968, 2(9): 12-16.
[3] Xu K, Hu W, Leskovec J, et al. How powerful are graph neural networks?[J]. arXiv preprint arXiv:1810.00826, 2018.
[4] 刘忠雨, 李彦霖, 周洋.《深入浅出图神经网络: GNN原理解析》.机械工业出版社.