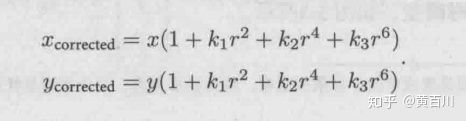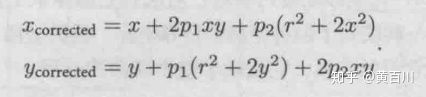相机标定：（1）相机模型

之前在进行标定时只是简单的会使用，调用OpenCV里边的函数，完成标定即可。并没有做过多深入的理解，今天趁着course学习把标定详细的记录一下，以下完全是个人理解如果有不对的地方欢迎批评指正。

公式推导见标定2（2）https://blog.csdn.net/m0_37957160/article/details/119613480

----------------------------正文----------------------------

0、前言

要想理解相机的标定过程，我们前期的准备工作就需要了解一下相机的模型，相机的成像原理，数码相机图像拍摄的过程实际上是一个光学成像的过程。相机的成像过程涉及到四个坐标系：世界坐标系、相机坐标系、图像坐标系、像素坐标系以及这四个坐标系的转换。

相机模型本人分为三个部分：

（1）理想透视模型——针孔成像模型

（2）透镜(多透镜)成像模型

（3）实际成像模型

1、针孔成像模型

相机将三维世界中的坐标点映射到二维图像平面的过程能够用一个几何模型进行描述。这个模型有很多种，其中最简单的称为针孔模型。所以通常说的针孔模型是一个极度简化的模型，其简化的对象是「单一的薄透镜作为镜头的相机」，其含义是：在适当程度近似后，一个单一的薄透镜作为镜头的相机，其光学行为一定程度上近似于一个针孔相机。

      

 

 

 

以上图片摘自OpenCV3教材。

 在现实生活中，针孔相机是由前方有 一个小洞（针孔）所构成。现实世界中源于某个物体的光线穿过此洞，会在摄像机的底板或图像平面上形成一幅倒立的图像。略为不便的是针孔相机的图像是倒置的。因此，我们换一种方式，对针孔前方图像平面的虚拟图像加以考虑。当然，从物理层面构造这样一种摄像机是不可能的，但是在数学层面上这与真实的针孔模型是等价的（除了针孔图像是倒置的以外）。

如下是针孔相机模型成像原理：

成像原理

2、透镜(多透镜)成像模型 

2.1单一薄透镜镜头的相机

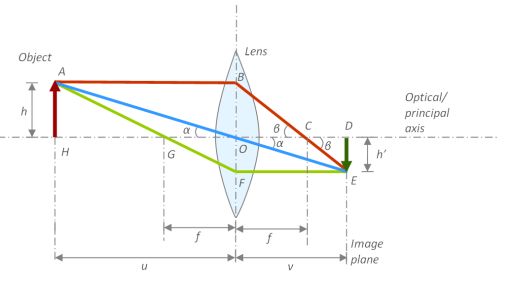
 对于右图：其中 u 为物距， f 为焦距，v 为相距。三者满足关系式：

                                                                 

相机的镜头是一组透镜，当平行于主光轴的光线穿过透镜时，会聚到一点上，这个点叫做焦点，焦点到透镜中心的距离叫做焦距 f。数码相机的镜头相当于一个凸透镜，感光元件就处在这个凸透镜的焦点附近，将焦距近似为凸透镜中心到感光元件的距离时就成为上面介绍的小孔成像模型。

PS：所谓相机感光元件其实就是数码单反相机中的一块很重要的电子元件。它的作用相当于传统相机中的胶卷，能够将光线转换成电荷信号，最终形成可见的电子格式，然后我们就可以把这些影像储存在数码相机的存储器上了。

对于上述左图，在中学学过，对于一个薄透镜而言，其光学行为完全由四个因素决定：光轴，光心，前焦点（物方焦点），后焦点（像方焦点）。在上图中，光轴就是图中水平的虚线，光心是 O 点，前焦点是 G 点，后焦点是 C 点。至于为什么需要区别对待两个焦点，是因为需要考虑到透镜两侧介质不同——虽然通常情况下透镜两侧都是空气罢了。只要确定了这四个要素，那么这个薄透镜的光学行为也完全确定了，对于空间中任何一个点（当然由于空间的对称性，我们不妨假定光线是从左至右传播的，这个意义下空间中任何一个点，作为「源」的角度来看都是唯一确定的），我们都可以找出在「透镜成像」这个变换之后对应的像。

从这四个要素出发，我们可以定义三条特殊的光线：1. 经过物点(从物体出发)，平行于光轴的光线，它经过透镜后将射向像方焦点（红色的线）；2. 经过物点与光心O的光线，其方向不变（蓝色的线）；3. 经过物点与物方焦点的光线，经过透镜后平行于光轴射出（青色的线）。（这三句话也就是老师总结的平行过焦，过心不变，过焦平行）

单一薄透镜的模型。这个模型的合理性是可以严格通过折射定律和数学推导进行证明的，证明过程不是这里的重点。重点是，我们从单纯数学的角度来看待这一模型，可以带来下一步的启发。

如果我们将空间中的物点看做原象，将「经过透镜成像」这一过程看做一个函数映射，将通过透镜成的像看做是函数映射的结果，那么薄透镜模型就在整个欧式空间中建立了一个映射的关系，而且是一一映射。考虑到无穷远点，那么经过简单地数学推导可以得出结论，这个映射关系是一个射影变换。借助齐次坐标，我们可以直接写成矩阵相乘的形式。仅以二维空间为例，物体经过一个透镜之后，在数学上就相当于左乘了一个矩阵，进行了一个射影变换。

 这里用带撇的量表示像方空间。

 也就是，从数学上说，对于物方空间（这里物方空间并非指的是透镜左边的半空间，而可以是整个空间）的点，经过左乘一个矩阵，就能变换到像方空间来。物方空间与像方空间通过这个矩阵（也就是透镜）建立了共轭的关系(这两个空间通过这个矩阵就建立了共轭关系)。

 PS：共轭(Conjugate)即为按一定的规律相配的一对。通俗点说就是孪生。

共轭：https://www.zhihu.com/question/264249324/answer/278477625

而前面说的四个要素，就是确立这个共轭关系所必不可少的条件，同时也是在这个映射下的某些特殊的共轭点。比如，如果一个点在某映射下保持不变，这就是「不动点Stationary point」，很明显，光心就是这个映射的不动点。再比如，物方的无穷远点其共轭点就是像方焦点，像方的无穷远点其共轭点就是物方焦点。当然，对于直线也有类似的共轭关系。

不动点：是一个函数术语，在数学中是指“被这个函数映射到其自身一个点”。在函数的有限次迭代之后回到相同值的点叫做周期点；不动点是周期等于 1 的周期点。（即一个点在影射下保持不变，这类点称为不动点）

在数学中，函数的不动点（Fixed point, or shortened to fixpoint, also knowns as invariant point），指的是在函数定义域内的某一个值，经过函数映射后的值还是其本身。

也就是说如果 c 是函数 f(c) 的不动点，则有：

                                                             

PS：我们对于单一薄透镜镜头的相机，才可以用针孔模型来建模。

2.2、实际工业相机多层镜片

对于工业上应用的多组透镜组成的镜头的情况：

既然物体经过一个透镜之后，在数学上就相当于左乘了一个矩阵，进行了一个射影变换，那么多片镜片的组合，实际上就是不断地将上一个镜片成的像作为下一个镜片的物，反复的运用不同的射影变换（当然，从上一个镜片转到下一个镜片的时候还包括了镜片之间的平移，这在齐次坐标下也是可以用一个射影变换的矩阵来表示的）——从数学上来说，就是不断左乘一系列的射影变换矩阵。而这些射影变换矩阵可以先相乘，得到一个总体的「系统矩阵」，这个系统矩阵就完全确定了这整个光学系统的行为。

一句话说明，由于考虑了镜片之间间隔（平移变换）的因素，这个系统矩阵需要由更多一些参数来刻画，具体来说，一个复杂的光学系统，其特性是由以下几个特征点来刻画的（Cardinal point (optics)）：

（1） 光轴（Optical Axis）：通过薄透镜两个球面球心的直线，叫做主光轴，也称主轴。

（2）节点（Nodal Point）：节点是一对共轭点，其表现为，所有经过物方（像方）节点的光线，方向不变地经过像方（物方）节点（如下图）；

节点概念介绍：https://v.youku.com/v_show/id_XOTE4Mjg5Njk2（3）主点（Principal Point）：

 （3）主点（Principal Point）：

（4）主平面（Principal Plane）:主平面是一对共轭平面，其表现为，所有与物方（像方）主平面相交的光线，对应的共轭光线都与像方（物方）主平面在相同高度相交。而主点就是主平面与光轴的交点，如下图，点P/P'以及竖直方向虚线代表的平面：

 （5）焦点（Focal Point）：平行于主轴的光线，通过镜头后相交于一点，这一相交点称为焦点。

在对焦准确的情况下，成像传感器与像方主平面之间的距离，应该是像距，当然，在物距趋向于无穷大的情况下，像距就等于焦距了，但一般情况下是比焦距略大一点的。这个直接套用中学时候学的凸透镜成像公式即可，只不过运用在实际镜头上时候，物距像距焦距等，都需要从各自对应的主点和主平面度量（特别注意互为共轭的两个主平面与物像的对应关系）。

3、实际成像模型

理想的透视模型是针孔成像模型，物和像会满足相似三角形的关系。但是实际上由于相机光学系统存在加工和装配的误差，透镜就并不能满足物和像成相似三角形的关系，所以相机图像平面上实际所成的像与理想成像之间会存在畸变。畸变属于成像的几何失真，是由于焦平面上不同区域对图像的放大率不同形成的画面扭曲变形的现象，这种变形的程度从画面中心至画面边缘依次递增，主要在画面边缘反映比较明显。为了减小畸变，拍摄图片时应尽量避免用镜头焦距的最广角端或最远端拍摄。实际的相机成像模型如下图所示：

其中 表示实际投影点的像平面坐标系下的物理坐标，表示理想投影点的像平面坐标系下的物理坐标。所以产生了畸变，畸变发生在相机坐标系转图像物理坐标系的过程中。操作的对象时相机坐标系。

3.1、畸变模型

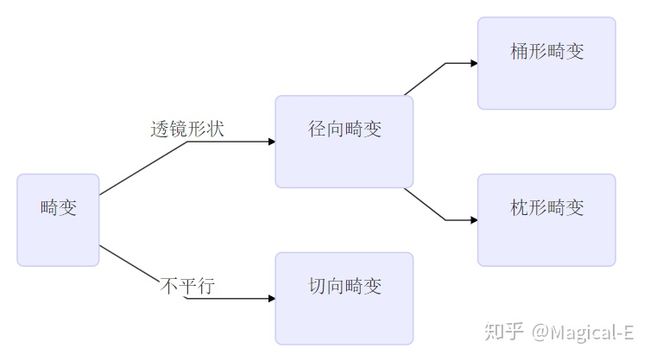
引起畸变的两个主要因素：（透镜由于制造精度以及组装工艺的偏差会引入畸变，导致原始图像的失真。）
1、透镜形状：径向畸变。
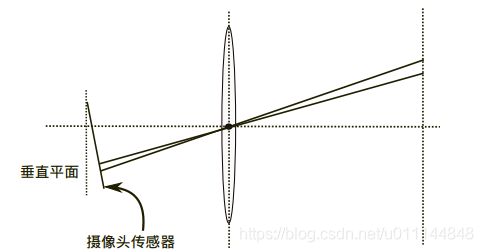
2、透镜与成像平面不平行：切向畸（如下右图）。

1. 径向畸变

顾名思义，径向畸变就是沿着透镜半径方向分布的畸变，产生原因是光线在原理透镜中心的地方比靠近中心的地方更加弯曲，这种畸变在普通廉价的镜头中表现更加明显，径向畸变主要包括桶形畸变和枕形畸变两种。以下分别是枕形和桶形畸变示意图：（右图为枕形，左图为桶形 ）

   对于象平面中的点，其畸变可由下图说明。dr:径向畸变dt:切向畸变（如上右图）

3.2、畸变参数（一般5个）

其中表示实际投影点的像平面坐标系下的物理坐标，表示理想投影点的像平面坐标系下的物理坐标。镜头的畸变模型可表示为：

 链接：https://blog.csdn.net/lsh_2013/article/details/47615309

3.2.1、透镜形状引起的畸变叫做径向畸变

 式中，是理想的无畸变的坐标（图像坐标系），为引入畸变效应所产生的坐标。都是已知的，因为标定板信息是已知的。

3.2.2、透镜安装与成像平面不平行引起的畸变叫做切向畸变

参考链接：https://www.zhihu.com/question/23512027