论文笔记《Spatio-Temporal Graph Structure Learning for Traffic Forecasting》
【论文】 Zhang Q, Chang J, Meng G, et al. Spatio-Temporal Graph Structure Learning for Traffic Forecasting[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2020, 34(01): 1177-1185.
【代码】 暂无
目录
- 1. Structure Learning Convolution
-
- 1.1 Formulation of SLC
- 1.2 Relationship Between SLC and CNN Methods
- 2. SLCNN for Traffic Forecasting
-
- 2.1 Global Structure Learning Convolution
- 2.2 Local Structure Learning Convolution
- 2.3 Pseudo Three Dimensional SLC
- 3. Experiments
本篇文章主要是解决如何建模复杂、动态的空间依赖性问题,作者认为现在用的图卷积神经网络存在以下几个问题:
- 使用预定义方法,或依赖于图结构的先验知识,这些并不能保证预测当前学习任务的准确性。
- 多利用局部图结构,忽略了远距离关系。
- 图结构一旦定义即固定,而实际上交通数据每时每刻都在变化,图结构也在变化。
因此,作者提出一种通用的图卷积公式Structure Learning Convolution (SLC),它能将结构信息显示地建模到卷积运算中。文章提出的SLCNN Layer部署了两个 SLC 分别用于捕捉全局和局部结构信息。同时,作者还将Pseudo three Dimensional convolution (P3D) networks 与 SLC 结合,用于捕捉时间依赖性。下面是对文章(模型)思路的梳理。
1. Structure Learning Convolution
1.1 Formulation of SLC
本节主要说明 Structure Learning Convolution(SLC) 基本思想,以及和普通卷积的异同点,这部分是本文模型的一个核心点,先记住构造思路就行,看上去还挺直观的。
作者认为卷积运算可看作是对输入信号的聚合操作,对于图结构数据,聚合操作不仅仅要聚合信号值,还要聚合图结构信息。因此,作者提出 SLC 表示为: y i = f ( ∑ e i j ∈ E S i j w j x j ) y_{i}=f\left(\sum_{e_{i j} \in \mathcal{E}} S_{i j} w_{j} x_{j}\right) yi=f(∑eij∈ESijwjxj),其中:
- f ( ⋅ ) f(·) f(⋅) 是激活函数;
- y i y_i yi 是节点 i i i 的输出信号;
- x i x_i xi 是节点 i i i 的输入数据,注意是embedded在图上的数据;
- e i j ∈ E e_{i j} \in \mathcal{E} eij∈E 表示 i / j i/j i/j 之间有边,其中 E \mathcal{E} E不是预定义的,是在训练中得到的。
- W \mathbf{W} W 是 n n n 维卷积核权重, w j w_j wj 是其中第 j j j 个元素。 w ∈ R C i n × C o u t × K max \mathbf{w} \in \mathbb{R}^{C_{i n} \times C_{o u t} \times K_{\max }} w∈RCin×Cout×Kmax 部分起到 convolutional kernel module的作用。
- S i j S_{i j} Sij 表示 i / j i/j i/j 之间的关联度。 S ∈ R N × K max \mathbf{S} \in \mathbb{R}^{N \times K_{\max }} S∈RN×Kmax 部分起到 structure module的作用,当 K max = N K_{\max }=N Kmax=N时表示全局图结构,反之是局部图结构。
1.2 Relationship Between SLC and CNN Methods
本节主要说明了之前提出的各种CNN方法,可以通过恰当定义 S S S ,然后通过SLC 的特定实例得到。仅以 普通卷积 和 Chebyshev Spectral CNN (ChebNet) 举例。
Classical CNN 定义为:
y i = f ( ∑ e i j ∈ E w j x j ) y_{i}=f\left(\sum_{e_{i j} \in \mathcal{E}} w_{j} x_{j}\right) yi=f⎝⎛eij∈E∑wjxj⎠⎞
这个你就可以看成是 SLC 中 S = 1 S=1 S=1(一种特例情况),因为普通卷积一视同仁地对待所有节点,不区分它们的位置信息。
ChebNet 定义为:
y = f ( ∑ j = 1 C α j T j ( L ~ ) x ) \mathbf{y}=f\left(\sum_{j=1}^{C} \alpha_{j} T_{j}(\tilde{\mathbf{L}}) \mathbf{x}\right) y=f(j=1∑CαjTj(L~)x)
其中, T j T_{j} Tj 表示切比雪夫多项式的第 j j j 项, α j \alpha_{j} αj 是相关系数,这个公式是 ChebNet 的基本定义。
【1】ChebNet 可参考 3.4 GCN-2
ChebNet 可以定义为不同 SLCs 的总和,其中每一个都可以将图结构定义为Laplacian矩阵的Chebyshev多项式,即对于第 j j j 个 SLC, S j = T j ( L ~ ) ∈ R N × N \mathbf{S}^{j}=T_{j}(\tilde{\mathbf{L}}) \in \mathbb{R}^{N \times N} Sj=Tj(L~)∈RN×N(时刻记住 S S S 表示图结构信息)。
2. SLCNN for Traffic Forecasting
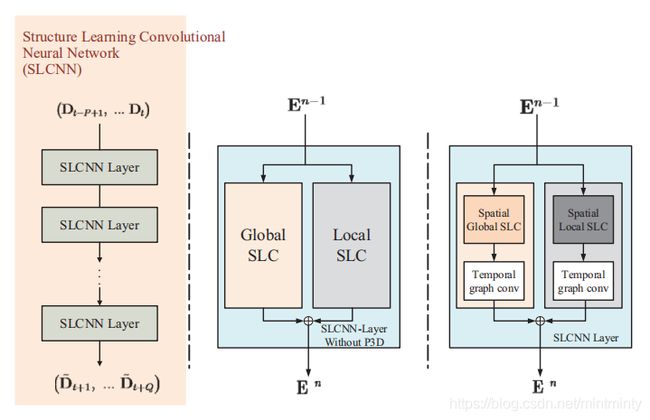
Structure Learning Convolutional Neural Network (SLCNN) 即为文章所提出的模型名称,左侧(橘色底色)部分是 SLCNN 整体结构,看上去还是比较简明的。模型的关键在于,不同于常规模型在网络的每一层都具有相同的结构(参数),该模型中每个SLCNN Layer都是不同的(学习到的参数不同),每一层都学习到不同的全局和局部图结构。那么,如何构造不同的SLCNN Layer?
每个 SLCNN Layer 由 global SLC 和 local SLC 组成:
- global SLC:用于捕捉全局图结构信息,不管节点是远是近
- local SLC:用于更好捕捉局部图结构信息
2.1 Global Structure Learning Convolution
利用 ChebNet 定义 global SLC,公式如下图,其中橘色部分为可学习的参数
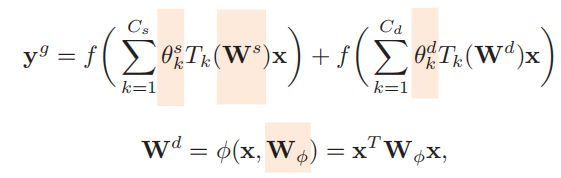
- T k ( ⋅ ) ∈ R N × N T_{k}(\cdot) \in \mathbb{R}^{N \times N} Tk(⋅)∈RN×N 是 k k k 阶切比雪夫多项式。要注意的是 使用的不再是预定义的邻接矩阵,其中 W s \mathbf{W}^{s} Ws 是静态的图邻接矩阵(学习得到), W d \mathbf{W}^{d} Wd 是动态的图邻接矩阵,但不是学习得到的参数,而是 ϕ ( x ) \phi(\mathbf{x}) ϕ(x) 的输出,其中 W ϕ \mathbf{W}_{\phi} Wϕ 是可学习的参数。
- 公式的前半部分是对全局静态结构建模(global static),后半部分是对全局动态结构建模(global dynamic)。
回忆1.1节作者提出的 SLC 的结构 y i = f ( ∑ e i j ∈ E S i j w j x j ) y_{i}=f\left(\sum_{e_{i j} \in \mathcal{E}} S_{i j} w_{j} x_{j}\right) yi=f(∑eij∈ESijwjxj),并且作者认为 ChebNet 可以用几个特定的 SLCs和 的形式表示,那么:
- 静态图结构部分表示为 S k = T k ( W s ) \mathbf{S}^{k}=T_{k}\left(\mathbf{W}^{s}\right) Sk=Tk(Ws)
- 动态图结构部分表示为 S k = T k ( W d ) \mathbf{S}^{k}=T_{k}\left(\mathbf{W}^{d}\right) Sk=Tk(Wd)
这部分和普通图卷积区别体现在:
- STGCN 和 DCRNN 是使用预定义的邻接矩阵,而 SLC 的邻接矩阵从数据中学习得到。
- STGCN 和 DCRNN 采用带阈值的高斯核定义邻接矩阵,这样一来它们能捕捉的就只能是局部图结构信息,本文通过 W s W d W^s W^d WsWd 体现的是全局的信息。
- 以往模型所有数据均共享同一个权重矩阵,而本文 W d W^d Wd 的值依赖于当前时刻的输入,所以不同输入数据具有的不同图结构信息也被体现了出来。
2.2 Local Structure Learning Convolution
local SLC 的定义和 global 的类似,橙色部分依旧是可学习的参数, B d B^d Bd 来自于当前输入数据的计算。
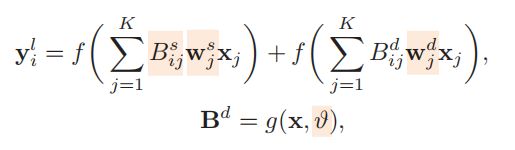
2.3 Pseudo Three Dimensional SLC
前面两节都是对空间维度的建模,本节提出 P3D-SLC 用于捕捉时间依赖性(也有空间)。
P3D 网络主要解决了两个问题:
- 解决原始3D卷积计算量过大的问题
- 仿照 resnet 构建更深的网络
P3D 网络大概做法:
原始3D卷积核333,现在把它拆成:
- 1 *3 *3的2D卷积,用于对空间关系建模
- 3 *1 *1的1D卷积,用于对时间关系建模
【2】Pseudo-3D Residual Networks 算法笔记
【3】Learning Spatio-Temporal Representation with Pseudo-3D Residual Networks
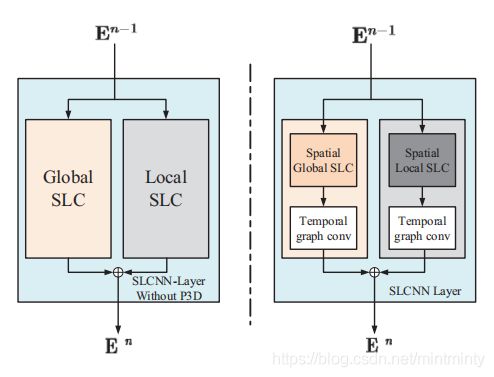
这部分说的很简略…实在不知道是怎么用的P3D = =,最后再看一下 SLC layer 图,左边这个是没有P3D的,有边有P3D。
3. Experiments
数据集:6个数据集
- PeMS-S / PeMS-BAY / METR-LA 是公共数据集
- BJF / BRF / BRF-L 是作者采集的数据
对比模型:
- Historical Average (HA), Auto-Regressive Integrated Moving Average(ARIMA), FC-LSTM, Feed-Forward Neural Network, GCNN methods, GWN, STGCN, DCRNN
- SLCNN-NP3D 没有P3D
- SLCNN-P 冻结了SLCNN的结构学习能力,只使用预定义的图形结构并删除P3D模块
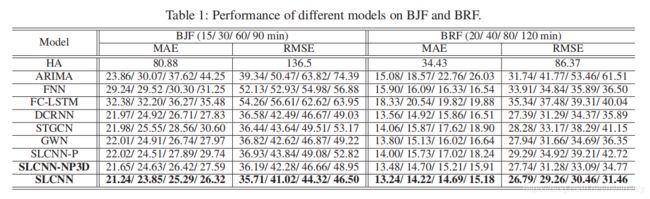
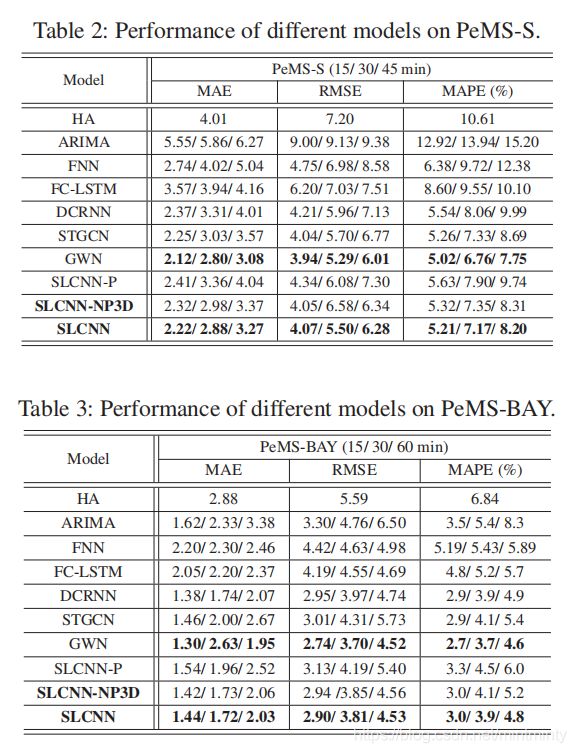
这两个数据集上 Graph wavenet 效果更好,好玄学…
除此之外,还验证了 Local and Global Graph 和 Static and Dynamic Graph 的有效性,以及计算效率。
