GBDT和xgboost原理、比较分析、面试总结
在介绍(Gradient Boosting Decesion Tree,GBDT)之前,需要先引入一些基础知识,从前向分步算法到梯度提升算法(Gradient Boosting)
文章目录
- 1 前向分步(Forward Step)
- 2 梯度提升(gradient boosting)
- 3 GBDT
- 4 XGBoost
-
- 为什么xgboost要用泰勒展开,优势在哪里?
- 5 面试点
-
- 5.1 GBDT的优缺点
- 5.2 GBDT训练的经验方法
- 5.3 GBDT和Xgboost的比较
- 5.4 XGBoost和LightGBM
-
- 1 LightGBM的产生背景
- 5.5 XGBoost如何处理缺失值?
1 前向分步(Forward Step)
对于加法模型: f ( x ) = ∑ m = 1 M β m b ( x ; γ m ) f(x)=\sum_{m=1}^{M} \beta_{m} b\left(x ; \gamma_{m}\right) f(x)=m=1∑Mβmb(x;γm)
其中, b ( x ; γ m ) \mathrm{b}(\mathrm{x;\gamma_m}) b(x;γm) 为基函数, γ m \gamma_\mathrm{~m} γ m 为基函数的参数, β m \beta \mathrm{m} βm 为基函数的系数。
损失函数为:
min β m , y m ∑ i = 1 N L ( y i , ∑ m = 1 M β m b ( x i ; γ m ) ) \min _{\beta_{m}, y_{m}} \sum_{i=1}^{N} L\left(y_{i}, \sum_{m=1}^{M} \beta_{m} b\left(x_{i} ; \gamma_{m}\right)\right) βm,ymmini=1∑NL(yi,m=1∑Mβmb(xi;γm))
对于这类问题,直接进行求解很复杂,优化的思想就是:因为学习的是加法模型,所以每次从前到后只学习一个基函数,逐步逼近目标的函数表达式,就可以简化优化复杂度。
具体的, 每步只需优化如下损失函数: min β , γ ∑ i = 1 N L ( y i , β b ( x i ; γ ) ) \min _{\beta, \gamma} \sum_{i=1}^{N} L\left(y_{i}, \beta b\left(x_{i} ; \gamma\right)\right) β,γmini=1∑NL(yi,βb(xi;γ))
逐步得到: min β m , γ m ∑ i = 1 N L ( y i , ∑ m = 1 M β m b ( x i ; γ m ) ) \min _{\beta_{m}, \gamma_{m}} \sum_{i=1}^{N} L\left(y_{i}, \sum_{m=1}^{M} \beta_{m} b\left(x_{i} ; \gamma_{m}\right)\right) βm,γmmini=1∑NL(yi,m=1∑Mβmb(xi;γm))
算法流程如下:
- 输入:
- 训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } \quad T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\} T={(x1,y1),(x2,y2),⋯,(xN,yN)}
- 损失函数 L ( y , f ( x ) ) L(y, f(x)) L(y,f(x)) 基函数集 { b ( x ; γ ) } \{b(x ; \gamma)\} {b(x;γ)}
- 输出:
- 加法模型 f ( x ) \mathrm{f}(\mathrm{x}) f(x)
- 1 初始化 f 0 ( x ) = 0 f_{0}(x)=0 f0(x)=0
- 2 对 m = 1 , 2 , … , M m=1, 2, \ldots, \mathrm{M} m=1,2,…,M
- a \mathrm{a} a 、极小化损失函数 ( β m , γ m ) = arg min β , γ ∑ i = 1 N L ( y i , f m − 1 ( x i ) + β m b ( x i ; γ m ) ) \quad\left(\beta_{m}, \gamma_{m}\right)=\arg \min _{\beta, \gamma} \sum_{i=1}^{N} L\left(y_{i}, f_{m-1}\left(x_{i}\right)+\beta_m b\left(x_{i} ; \gamma_m\right)\right) (βm,γm)=argβ,γmini=1∑NL(yi,fm−1(xi)+βmb(xi;γm))
- 得到参数 β m , γ m \beta_{m}, \quad \gamma_{m} βm,γm
- b、更新 f m ( x ) = f m − 1 ( x ) + β m b ( x ; γ m ) f_{m}(x)=f_{m-1}(x)+\beta_{m} b\left(x ; \gamma_{m}\right) fm(x)=fm−1(x)+βmb(x;γm)
- 3 得到加法模型
f ( x ) = f M ( x ) = ∑ m = 1 M β m b ( x ; γ m ) \quad f(x)=f_{M}(x)=\sum_{m=1}^{M} \beta_{m} b\left(x ; \gamma_{m}\right) f(x)=fM(x)=m=1∑Mβmb(x;γm)
2 梯度提升(gradient boosting)
提升树通过加法模型和前向分步算法实现学习的优化过程,比如损失函数是平方损失时:
L ( y , f t − 1 ( x ) + h t ( x ) ) = ( y − f t − 1 ( x ) − h t ( x ) ) 2 = ( r − h t ( x ) ) 2 \begin{gathered} L\left(y, f_{t-1}(x)+h_{t}(x)\right) \\ =\left(y-f_{t-1}(x)-h_{t}(x)\right)^{2} \\ =\left(r-h_{t}(x)\right)^{2} \end{gathered} L(y,ft−1(x)+ht(x))=(y−ft−1(x)−ht(x))2=(r−ht(x))2
可以看到,弱学习器 h t ( x ) h_t(x) ht(x)要拟合的的是残差r,当损失函数是平方损失和指数损失函数时,每一步的优化都是很简单。
但对于一般损失函数(比如对数损失函数)而言,往往每一步的优化并不那么容易,弱学习器要拟合的对象就很难推理出来。针对这一问题,freidman提出了梯度提升算法。 根据梯度下降的思想,使用负梯度方向作为表示残差 \color{red}根据梯度下降的思想,使用负梯度方向作为表示残差 根据梯度下降的思想,使用负梯度方向作为表示残差
在Gradient Boosting中,采取分层学习的方法,通过m个步骤来得到最终模型 f ( x ) f(x) f(x),
- 第m步学习一个较弱的模型 f m ( x ) f_m(x) fm(x)
- 在第m+1步时,不直接优化 f m ( x ) f_m(x) fm(x),而是学习一个基本模型 h ( x ) h(x) h(x),使得其拟合前m个基分类器的残差项,这样就会使m+1步的模型预测值 f m + 1 = f m + h ( x ) f_{m+1}=f_m+h(x) fm+1=fm+h(x)更接近于真实值y,因而目标变成了如何找到 h ( x ) = f m + 1 ( x ) − f m ( x ) h(x)=f_{m+1}(x)-f_m(x) h(x)=fm+1(x)−fm(x)。 根据梯度下降的思想,使用负梯度方向作为表示残差 \color{red}根据梯度下降的思想,使用负梯度方向作为表示残差 根据梯度下降的思想,使用负梯度方向作为表示残差
- 最终: f ( x ) = ∑ i = 1 M γ i h i ( x ) + c o n s t a n t f(x)=\sum_{i=1}^{M}\gamma_ih_i(x)+constant f(x)=∑i=1Mγihi(x)+constant
3 GBDT
在Gradient Boosting的基础上,使用CART树作为基分类器,就是GBDT。算法流程如下:
- (1) 初始化弱分类器 f 0 ( x ) f_{0}(x) f0(x) :
f 0 ( x ) = argmin c ∑ i = 1 N L ( y i , c ) f_{0}(x)=\operatorname{argmin}_{c} \sum_{i=1}^{N} L\left(y_{i}, c\right) f0(x)=argminci=1∑NL(yi,c) - (2) 对每棵树 m = 1 , 2 , 3 … … . M m=1,2,3 \ldots \ldots . M m=1,2,3…….M, 进行如下计算:
-
对每个样本 i = 1 , 2 , 3 … … . . N \mathrm{i}=1,2,3 \ldots \ldots . . \mathrm{N} i=1,2,3……..N ,计算残差:
r i m = − [ ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f m − 1 ( x ) r_{i m}=-\left[\frac{\partial L\left(y_{i}, f\left(x_{i}\right)\right)}{\partial f\left(x_{i}\right)}\right]_{f(x)=f_{m-1}(x)} rim=−[∂f(xi)∂L(yi,f(xi))]f(x)=fm−1(x) -
将上步计算的残差作为样本的新标签,并将 ( x i , r i m ) i = 1 , 2 , 3 … N \left(x_{i}, r_{i m}\right) \mathrm{i}=1,2,3 \ldots \mathrm{N} (xi,rim)i=1,2,3…N 作为下一棵树的训练数据,然后计算平方误差寻找样本的最佳分裂点(特征节点),构建本棵树 f m ( x ) f_{m}(x) fm(x) ,树的叶子节点为 R j m R_{j m} Rjm j = 1 , 2 , 3 … … , J j=1,2,3 \ldots \ldots, J j=1,2,3……,J, 其中$J为树叶子节点个数。
-
计算树的叶子节点 R j m j = 1 , 2 , 3 … . . R_{j m} \mathrm{j}=1,2,3 \ldots . . Rjmj=1,2,3….. 的最佳拟合值
Υ j m = argmin Υ ∑ x i ⊆ R j m L ( y i , f m − 1 ( x i ) + Υ ) \Upsilon_{j m}=\operatorname{argmin}_{\Upsilon} \sum_{x_{i} \subseteq R_{j m}} L\left(y_{i}, f_{m-1}\left(x_{i}\right)+\Upsilon\right) Υjm=argminΥxi⊆Rjm∑L(yi,fm−1(xi)+Υ) -
更新强学习器
f m ( x ) = f m − 1 ( x ) + ∑ j = 1 J Υ j m I ( x i ⊆ R j m ) f_{m}(x)=f_{m-1}(x)+\sum_{j=1}^{J} \Upsilon_{j m} I\left(x_{i} \subseteq R_{j m}\right) fm(x)=fm−1(x)+j=1∑JΥjmI(xi⊆Rjm)
-
- (3) 得到最终学习器
M ( x ) = f 0 ( x ) + ∑ m = 1 M ∑ i = 1 J Υ j m I ( x i ⊆ R j m ) M(x)=f_{0}(x)+\sum_{m=1}^{M} \sum_{i=1}^{J} \Upsilon_{j m} I\left(x_{i} \subseteq R_{j m}\right) M(x)=f0(x)+m=1∑Mi=1∑JΥjmI(xi⊆Rjm)
 关于GBDT的更多解读:https://zhuanlan.zhihu.com/p/144855223
关于GBDT的更多解读:https://zhuanlan.zhihu.com/p/144855223
https://www.cnblogs.com/jiangxinyang/p/9248154.html
4 XGBoost
XGBoost是GBDT的工程化实现,由陈天奇开源的GBDT实现平台。
为什么xgboost要用泰勒展开,优势在哪里?
xgboost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得函数做自变量的二阶导数形式, 可以在不选定损失函数具体形式的情况下, 仅仅依靠输入数据的值就可以进行叶子分裂优化计算, 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了xgboost的适用性, 使得它按需选取损失函数, 可以用于分类, 也可以用于回归。

在GBDT中我们通过求损失函数的负梯度(一阶导数),利用负梯度替代残差来拟合树模型。在XGBoost中直接用泰勒展开式将损失函数展开成二项式函数(前提是损失函数一阶、二阶都连续可导,而且在这里计算一阶导和二阶导时可以并行计算)
///太难了看不懂公式,留着下次看吧。
5 面试点
5.1 GBDT的优缺点
GBDT的主要优点:
-
可以灵活的处理各种类型的数据(Cart二分树,所以对离散连续值都可以)
-
泛化能力和表达能力都可以。
-
使用了一些健壮的损失函数,如huber,可以很好的处理异常值。
-
具有很好的可解释性和鲁棒性。
GBDT的缺点:
- 由于基学习器之间的依赖关系,难以并行化处理,不过可以通过子采样的SGBT来实现树内部的并行。
- 高维稀疏的数据集不如SVM和NN
5.2 GBDT训练的经验方法
-
树的深度 J J J 一般在 [ 4 , 8 ] [4,8] [4,8] 之间
-
Shrinkage: 定义学习率 v v v ,使得 F m + 1 = F m + v ⋅ γ m h m ( x ) F_{m+1}=F_{m}+v \cdot \gamma_{m} h_{m}(x) Fm+1=Fm+v⋅γmhm(x) ,其中 v ∈ ( 0 , 1 ] v \in(0,1] v∈(0,1]
-
使用随机梯度提升的方法,速度更快,还可以使用OOB error指标来评估模型的效果
-
防止过拟合的几种方法
- 迭代次数 M M M 取一个较为合适的值
- 如果决策树的某次划分使得节点上的实例数小于某个阈值,则丟弃该划分
- 树的复杂度作为惩罚项
-
GBDT的改进
(1) 在预测阶段,每个CART是独立的,因此可以并行计算。另外,得益于决策树的高效率,GBDT在预测阶段的计算速度是非常快的。(2) 在训练阶段,GBDT里的CART之间存在依赖,无法并行,所以GBDT的训练速度是比较慢的。人们提出了一些方法,用来提升这个阶段的并行度,以提升学习速度。
(3) 这里为了简单,使用了残差平方和作为损失函数,实际上还可以使用绝对值损失函数、huber损失函数等,从而让GBDT在鲁棒性等方面得到提升。
(4) GBDT的学习能力非常强,容易过拟合。大部分时候,我们都会给目标函数添加针对模型复杂度的惩罚项,从而控制模型复杂度
5.3 GBDT和Xgboost的比较
-
GBDT是算法,XGBoost是工程实现
-
GBDT以CART作为基分类器,xgboost还支持线性分类器。
-
XGBoost在损失函数中显式的加入了正则项,有利于防止模型过拟合。
-
节点分裂的方式不同,GBDT是用的gini系数,xgboost是经过优化推导后的gini指数.
-
传统GBDT在优化时只用到一阶导数信息,xgboost则对代价函数进行了二阶泰勒展开,同时用到了一阶和二阶导数。下降速度更快。
-
GBDT使用全部的数据,Xgboost类似于随机森林的策略,可以对数据进行采样(特征采样)。
-
GBDT无法对缺失值处理,后者可以自动学习缺失值的处理策略。
-
Xgboost工具支持并行。boosting不是一种串行的结构吗?怎么并行的?
注意xgboost的并行不是tree粒度的并行,xgboost也是一次迭代完才能进行下一次迭代的(第t次迭代的代价函数里包含了前面t-1次迭代的预测值)。xgboost的是在特征粒度并行上的。
- 我们知道,决策树的学习最耗时的一个步骤就是对特征的值进行排序(因为要确定最佳分割点),xgboost在训练之前,预先对数据进行了排序,然后保存为block结构,后面的迭代中重复地使用这个结构,大大减小计算量,这个block结构也使得并行成为了可能。
- 在进行节点的分裂时,需要计算每个特征的增益,最终选增益最大的那个特征去做分裂,那么各个特征的增益计算就可以开多线程进行。
5.4 XGBoost和LightGBM
1 LightGBM的产生背景
BDT和XGBoost在训练过程中每次迭代树模型时,都会多次遍历整个数据集,这个操作比较耗时,同时如果将数据集全部放入内存,又会占用过多的内存资源,特别是工业界的训练数据量。
所以基于以上的考虑,微软提出了LightGBM算法,算法原理方面和GBDT和XGBoost是一致的,都是对负梯度方向残差的拟合。
LightGBM相比较于XGBoost的改进之处在于:
-
XGBoost中树的生长采用了level-wise的方式,然而LightGBM使用的是带有深度限制的leaf-wise的方式。
level-wise在分裂节点过程中,会一层一层的分裂叶子节点,同层的叶子节点不加区分地对待,所以某些叶子节点有可能对其分裂增益并不大,从而造成了一些资源和性能浪费。
leaf-wise在分裂节点过程中,会有有限选择增益比较大的叶子节点对其进行分裂,所以leaf-wise相比level-wise会有更高的精度。
不足的是:相对level-wise,leaf-wise其过拟合风险也会更高,所以需要用树的深度加以限制。
-
分裂节点算法不同
XGBoost采用了pre-sort预排序算法,LightGBM采用了histogram直方图算法。pre-sort算法会将每个特征的所有数值进行排序,然后对每个分裂点计算信息增益,最终找到信息增益最大的特征和对应的分裂点,进行分裂该叶子节点。
虽然这种做法能够获得比较精确的分裂点,但是,需要保存排序好的每个特征的数据,所以内存占用是原始数据的两倍。并且在计算时需要对每个分裂点计算信息增益,所以计算量也比较大。histogram算法会将每个特征进行量化,使得连续相近的值落入不同的桶中,在分裂节点的时候,我们只需要针对每个桶中的离散值作为分裂节点计算信息增益,然后选择信息增益最大的特征和分裂点,进行分裂该叶子节点。histogram算法只需要保存每个特征的离散值,不需要保存pre-sort的预排序结果,所以内存使用会减少很多。另一方面,其每个分裂点的选择从pre-sort的全体特征数据减少为桶的数量,因为桶的数量会远远少于特征数量,所以会大幅提升训练效率。最后使用桶量化的概念相当于正则化,所以会有更高的泛化准确率。
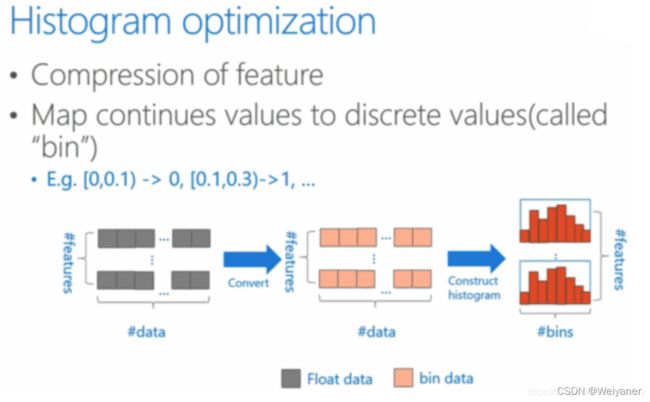
不足的是:histogram算法进行了数据量化,所以在每次分裂时,无法保证获取最准确的特征和相应分裂点。如果桶的数量比较少,有可能会造成欠拟合。
5.5 XGBoost如何处理缺失值?
XGBoost对比GBDT很大的一个优势就是如何处理可以处理缺失值。在决策树中,一般认为对缺失值不敏感,个人理解这是因为在计算节点分裂时,用的是信息增益等等的指标,这些指标是基于信息熵,因此树模型对于缺失值都不敏感。
所以一般树模型中,缺失值可以不处理,或者就是常规方法处理,比如RF作者论文提到了两种方式
在XGBoost中,陈天奇提到了一种缺失值处理方式,在进行节点分裂时,不考虑缺失值的影响,利用完整数据节点分裂,然后将该缺失值数据分别放进左右子树,计算增益值,看哪个增益大就将该数据放到该子树。


