- vscode怎么装python_vscode如何安装python
vscode安装python的方法:1、在vscode的扩展中输入"extinstallpython"安装python插件打开VScode,Ctrl+p输入"extinstallpython",搜索时间可能会比较长安装过程不能停止,否则重新安装;2、在配置文件“settings.json”修改python的安装路径修改用户设置-settings.json,将"python.pythonPath":
- 机器学习算法之回归算法
福葫芦
机器学习回归算法
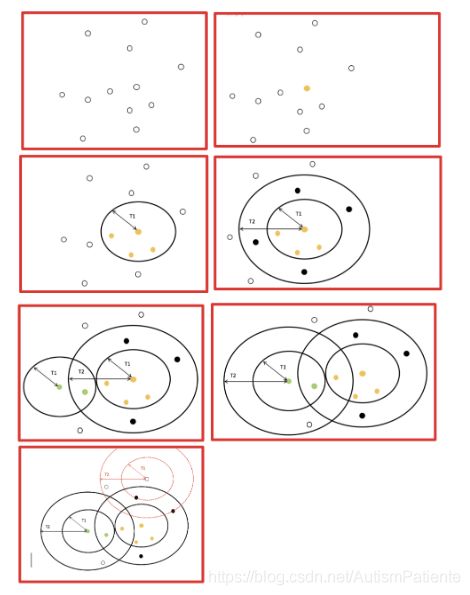
一、回归算法思维导图二、算法概念、原理、应用场景和实例代码1、线性回归1.1、概念线性回归算法是一种统计分析方法,用于确定两种或两种以上变量之间的定量关系。线性回归算法通过建立线性方程来预测因变量(y)和一个或多个自变量(x)之间的关系。其基本形式为y=wx+e,其中w是权重,x是自变量,e是误差项。1.2、算法原理线性回归算法的核心在于找到最佳的拟合直线,使得预测值与实际值之间的误差最小。
- 7篇1章7节:机器学习算法解读,与数值预测回归模型构建
MD分析
用R探索医药数据科学机器学习算法回归r语言数据挖掘
机器学习是当今数据分析和人工智能的核心工具之一,其算法广泛应用于分类、回归、排序和推荐等领域。本篇将详细讲解机器学习的四大经典算法类型,并以回归问题为例深入探讨数值预测的关键步骤,包括数据准备、线性回归模型构建、模型预测及误差评估,帮助读者更系统地理解和掌握机器学习的基础知识及实际应用。一、机器学习的算法在数据科学和人工智能的浪潮中,机器学习算法成为了解决各种数据问题的关键工具。机器学习主要处理四
- 关于python的一些面试题
1.技术面试题(1)TCP与UDP的区别是什么?答:在工作机制上TCP采用三次握手四次挥手的机制保障信息传递的稳定性,更适合文件的传输和下载。而UDP采用的是直接传输和直接接受的机制提高信息传递的高效性,更适合点对点的实时交流的环境。(2)DHCP和DNS的作用是什么?答:DHCP相当于网络中的智能管家,他会自动将局域网内的设备进行配置包括但不限于:IP地址、子网掩码、DNS服务器地址。而DNS相
- python里面ca_Python SSL服务器提供中间CA证书
洗心岛
python里面ca
我使用Python(2.7)SSL模块编写一些服务器代码,如下所示:ssock=ssl.wrap_socket(sock,ca_certs="all-ca.crt",keyfile="server.key",certfile="server.crt",server_side=True,ssl_version=ssl.PROTOCOL_TLSv1)全部-约阴极射线管'包含签名CA证书和根CA证书:-
- 服务器搭建python响应https,python实现简单的https服务器
以下提供一个简单的方式快速部署一个https服务器,用于非生产环境的测试使用,如果是正式的生产环境,考虑到性能安全等因素,就不要使用这个了。1、使用pyOpenSSL库:#coding:utf-8fromBaseHTTPServerimportHTTPServer,BaseHTTPRequestHandlerfromSocketServerimportThreadingMixInfromSocke
- Leetcode刷题笔记——哈希表篇
code_lover_forever
Leetcode刷题笔记leetcode笔记散列表python
Leetcode刷题笔记——哈希表篇一、哈希表在面试中的高频考题第一题:两数之和Leetcode1:两数之和:中等题(详情点击链接见原题)给定一个整数数组nums和一个整数目标值target,请你在该数组中找出和为目标值target的那两个整数,并返回它们的数组下标python代码解法classSolution:deftwoSum(self,nums:List[int],target:int)->
- Various ways to integrate Python and C (C++)
a13393665983
c/c++人工智能python
VariouswaystointegratePythonandC(C++)KoichiTamura'sblog:VariouswaystointegratePythonandC(C++)VariouswaystointegratePythonandC(C++)ThisisoriginallywhatIwroteinamailIsenttoafriendofmine.Imodifieditalitt
- How to setup a Mac with Python dev tools
whackw
macmac
HowtosetupaMacwithPythondevtoolsNotesforhowtosetupa64-bitMacwithimportantPythondevelopmenttoolsDeprecated–clickhereforupdatedpageforYosemiteversionCreatedbyTrondKristiansenon27.7.2009,andlastupdated05
- 理解module, script, library, package in Python
ikeepo
#小白学Pythonmodulelibraryscriptpackagesetup
OverviewPythonmodulesandPythonpackagesaretwomechanismsthatfacilitatemodularprogramming.AscriptisaPythonfilethat’sintendedtoberundirectly.AmoduleisaPythonfilethat’sintendedtobeimportedintoscriptsorothe
- Python 服务器端与客户端的加密通信(SSL/TLS)解析
现实逃脱计划TA
pythonssl网络
```htmlPython服务器端与客户端的加密通信(SSL/TLS)解析在当今互联网时代,数据安全变得越来越重要。为了保护数据在传输过程中的安全,使用SSL/TLS协议进行加密通信成为了一种常见的做法。本文将详细介绍如何在Python中实现服务器端和客户端之间的SSL/TLS加密通信。什么是SSL/TLS?SSL(SecureSocketsLayer)和TLS(TransportLayerSec
- python教程修订版
Ethan learn English
python
9/23Inthiscourse,I'mgoingtoteachyoueverythingyouneedtoknowtogetstartedprogramminginPython.Now,Pythonisoneofthemostpopularprogramminglanguagesoutthere在众多的……中.Andit'sbyfar目前为止oneofthemostsõughtafter受欢迎的
- Three ways to run a python script file
captainOO7
python
Pythonoffersthreedistinctwaystorunascriptormodule,andeachoneaffectssys.path,__name__,andimportbehaviorinsubtlebutimportantways.Let’sbreakthemdownclearly:TheThreeWaystoRunPythonCode1.DirectScriptExecut
- Python自动化神器:Pyautogui库实战指南
码界奇点
Pythonpython自动化开发语言python3.11ui
欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。持续学习,不断总结,共同进步,为了踏实,做好当下事儿~非常期待和您一起在这个小小的网络世界里共同探索、学习和成长。✨✨欢迎订阅本专栏✨✨TheStart点点关注,收藏不迷路文章目录1.PyAutoGUI简介1.1什么是PyAutoGUI?1.2安装
- tensorflow sigmoid_cross_entropy_with_logits 函数解释及公式推导
CrazyWolf_081c
tensorflowsigmoid_cross_entropy_with_logits函数解释及公式推导tensorflow官方文档解释参考pytorch--BCELosspytorch--BCELoss解释参考定义在tensorflow/python/ops/nn_impl.py.功能:计算在给定logits和label之间的sigmoidcrossentropy。测量离散分类任务中的概率误差,
- vue中实现验证码输入
结城
vue验证码vue输入框
vue验证码input输入解决焦点切换有点晚了就不吐槽了,咱还是把代码上了,赶紧洗澡,养好精神明天努力上班!!!想学node,想学react,想精进webpack,想vue学的更好一点,了解底层代码,学算法,学计算机原理,想写自己的博客网站…这是一条学无止境的路,没办法要恰饭效果html部分js部分exportdefault{props:{inputNums:{type:Number,defaul
- 写一个空调风机时长统计系统
需求:通过python图形化程序需要实现空调风机的时长统计。界面功能介绍:该空调系统分为8页,通过右上角左右翻页的方式进行页面切换,翻页按钮是翻到最后一页后只能通过上一页往前面,同理第一页也是这样。做了颜色采样,采样而且每页的风机数量是不同的,灰色:#515151RGB:818181绿色:#1bf928RGB:2724940底色:#033047RGB:34871灰色是未开机状态、绿色是开机状态、底
- 超简单linux上部署Apache
悟空骑猪看电影
apachelinux运维网络
1.Apache是什么?Apache是世界上最流行的开源Web服务器软件,由Apache软件基金会维护。主要功能:接收客户端(如浏览器)的HTTP请求,返回网页、图片等静态/动态资源。特点:跨平台(Linux、Windows、macOS)模块化设计(按需加载功能)支持多语言扩展(PHP、Python等)高稳定性和安全性2.核心架构与工作原理多进程模型(MPM)Prefork:多进程模式,每个请求由
- nodejs关于后端服务开发的探究
墨水白云
node.js
前提在当前的环境中关于webserver的主流开发基本上都是java、php之类的,其中javaspring系列基本上占了大头,而python之流也在奋起直追,但别忘了nodejs也是可以做这个服务的,只是位置有点尴尬,现在就来探究下nodejs做webserver的当前现状。nodejs简介Node.js是一个基于ChromeV8引擎的JavaScript运行环境。Node.js使用了一个事件驱
- 基于逻辑回归的图像二分类算法实现(Pytorch版)
哎呦哥哥、
图像分类pytorch逻辑回归分类
基于逻辑回归的图像二分类算法实现(Pytorch版)数据集模型代码数据集链接:FastFoodClassificationDataset我们只使用Burger和Pizza这两类。模型代码importtorchimporttorch.nnasnnfromtorchvision.models.utilsimportload_state_dict_from_urlmodel_urls={'resnet5
- Python自动操作GUI神器PyAutoGUI
小菜菜-K
PYTHON
日常使用计算机,命令行程序可以说是为批量操作文件而生,但作为普通用户,最多的还是通过鼠标键盘操作形形色色的图形界面程序。试想下面一个场景:有成千上万个文件,都需要通过图形界面进行同样的一套编辑、保存工作,靠手工一遍一遍地重复做,累死人不说,时间久了必然出现错误,作为程序猿,怎么能忍重复3次以上的工作,必须利用程序自动化。要想图形界面也能像命令行程序那样精确控制,就需要GUI自动化工具了。不得不赞P
- Python练习(7)Python模块与方法:20道核心实战练习题(含答案与深度解析)(上)
目录引言基础篇(5题)练习1:模块导入方式对比练习2:模块别名应用练习3:条件导入模块练习4:模块搜索路径管理练习5:包结构初始化进阶篇(5题)练习6:模块重载机制练习7:类方法与静态方法区分练习8:魔术方法应用练习9:模块级变量作用域练习10:装饰器实现方法注册高级技巧篇(5题)练习11:动态模块导入练习12:命名空间包练习13:模块卸载陷阱练习14:元类方法控制练习15:上下文管理器方法实战案
- python启动其他程序或命令(pandoc)
SUN_SU3
python
编写python脚本时,有些功能由其他程序执行,直接在python脚本中启动对应的程序或命令执行即可,现记录用过的几种方法:查看程序的安装目录:whichpandoc1)subprocess:importsubprocessa=subprocess.Popen(['/opt/***/pandoc','/home/***/test.docx','-o','/home/***/test.html'])
- 全国青少年软件编程(Python)等级考试四级考试真题2024年3月——持续更新.....
owbc_
电子学会(python)三四级考试真题及答案(持续更新)python算法开发语言青少年编程
青少年软件编程(Python)等级考试试卷(四级)分数:100题数:38一、单选题(共25题,共50分)1.运行如下代码,若输入整数3,则最终输出的结果为?()deff(x):ifx==1:s=1else:s=f(x-1)*xreturnsn=int(input(“请输入一个大于1的整数:”))print(f(n)+f(n-1))A.2B.4C.8D.16标准答案:C试题解析:由于f(3)=f(2
- 【亲测免费】 PyPandoc 项目常见问题解决方案
PyPandoc项目常见问题解决方案基础介绍PyPandoc是一个为Pandoc提供的Python薄壳包装器。Pandoc是一个通用的文档转换工具,能够将标记格式的文档转换为多种格式。PyPandoc主要使用Python编程语言,旨在简化Pandoc在Python项目中的使用。新手常见问题及解决步骤问题1:如何安装PyPandoc问题描述:新手在使用PyPandoc时,首先需要了解如何正确安装。解
- 青少年人工智能Python编程水平测试四级 模拟试卷9 试题解析
编程小伙伴测评网
YCL试题详解python开发语言少儿编程青少年编程算法数据结构排序算法
1、以下选项中,说法正确的是?()A、条件1and条件2,表示条件满足其中1个即可B、条件1or条件2,表示2个条件需要同时满足C、and和or不能在一个条件表达式中同时使用D、andor一般和if语句搭配使用正确答案:D试题解析:and是逻辑与,同时满足结果才满足;or是逻辑或,满足一个结果就是满足;
- 青少年人工智能Python编程水平测试四级 模拟试卷5 试题解析
编程小伙伴测评网
YCL试题详解python开发语言少儿编程青少年编程算法推荐算法
【单选题】(每题2分)1、运行下列代码后,输入4,输出的结果是?()num_1=input()num_2="3"print(num_1+num_2)A、7B
- 十年老Python程序员:给我一个链接,没有我不能爬的视频,只有我顶不住的视频
IT孔乙己
一、写在前面真的,为什么别人发游戏这么多人看,我发了两次了加起来才一百个。算了算了,不整游戏了,反正你们也不爱看~python今天来试试把头条上扭腰上热门的那些妹子爬一爬,不知道我顶不顶得住~python二、准备工作1、使用的环境python3.8pycharm2021.2专业版2、要用的第三方模块seleniumrequestsparsel三、大致流程鉴于你们不喜欢我啰嗦,但是流程呢,我还是要给
- Python中win32com的用法详解:自动化办公与COM交互的利器
detayun
Pythonpython自动化交互win32
在Python自动化办公场景中,win32com模块凭借其与WindowsCOM(ComponentObjectModel)的深度集成能力,成为操控MicrosoftOffice、工业设备甚至第三方软件的核心工具。本文将通过实战案例、技术细节和避坑指南,系统解析这一模块的核心用法。一、核心功能与安装配置1.1模块定位与优势win32com是pywin32扩展包的核心组件,其核心价值在于:跨软件交互
- O (1) 空间搞定链表:穿针引线法核心技巧与例题
无聊的小坏坏
算法链表c++算法
文章目录穿针引线法的核心思想基础应用:链表反转1.全链表反转2.部分链表反转高级应用:链表重排穿针引线法的设计模式常见问题解决方案1.K个一组反转链表2.环形链表检测在链表操作的世界里,"穿针引线"是一种优雅而高效的技巧,它通过精准的指针操作,像缝纫一样重新连接节点,解决各种复杂的链表问题。这种技巧不依赖额外数据结构,空间复杂度仅为O(1),是算法面试中的必备技能。穿针引线法的核心思想指针即针线:
- 关于旗正规则引擎中的MD5加密问题
何必如此
jspMD5规则加密
一般情况下,为了防止个人隐私的泄露,我们都会对用户登录密码进行加密,使数据库相应字段保存的是加密后的字符串,而非原始密码。
在旗正规则引擎中,通过外部调用,可以实现MD5的加密,具体步骤如下:
1.在对象库中选择外部调用,选择“com.flagleader.util.MD5”,在子选项中选择“com.flagleader.util.MD5.getMD5ofStr({arg1})”;
2.在规
- 【Spark101】Scala Promise/Future在Spark中的应用
bit1129
Promise
Promise和Future是Scala用于异步调用并实现结果汇集的并发原语,Scala的Future同JUC里面的Future接口含义相同,Promise理解起来就有些绕。等有时间了再仔细的研究下Promise和Future的语义以及应用场景,具体参见Scala在线文档:http://docs.scala-lang.org/sips/completed/futures-promises.html
- spark sql 访问hive数据的配置详解
daizj
spark sqlhivethriftserver
spark sql 能够通过thriftserver 访问hive数据,默认spark编译的版本是不支持访问hive,因为hive依赖比较多,因此打的包中不包含hive和thriftserver,因此需要自己下载源码进行编译,将hive,thriftserver打包进去才能够访问,详细配置步骤如下:
1、下载源码
2、下载Maven,并配置
此配置简单,就略过
- HTTP 协议通信
周凡杨
javahttpclienthttp通信
一:简介
HTTPCLIENT,通过JAVA基于HTTP协议进行点与点间的通信!
二: 代码举例
测试类:
import java
- java unix时间戳转换
g21121
java
把java时间戳转换成unix时间戳:
Timestamp appointTime=Timestamp.valueOf(new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date()))
SimpleDateFormat df = new SimpleDateFormat("yyyy-MM-dd hh:m
- web报表工具FineReport常用函数的用法总结(报表函数)
老A不折腾
web报表finereport总结
说明:本次总结中,凡是以tableName或viewName作为参数因子的。函数在调用的时候均按照先从私有数据源中查找,然后再从公有数据源中查找的顺序。
CLASS
CLASS(object):返回object对象的所属的类。
CNMONEY
CNMONEY(number,unit)返回人民币大写。
number:需要转换的数值型的数。
unit:单位,
- java jni调用c++ 代码 报错
墙头上一根草
javaC++jni
#
# A fatal error has been detected by the Java Runtime Environment:
#
# EXCEPTION_ACCESS_VIOLATION (0xc0000005) at pc=0x00000000777c3290, pid=5632, tid=6656
#
# JRE version: Java(TM) SE Ru
- Spring中事件处理de小技巧
aijuans
springSpring 教程Spring 实例Spring 入门Spring3
Spring 中提供一些Aware相关de接口,BeanFactoryAware、 ApplicationContextAware、ResourceLoaderAware、ServletContextAware等等,其中最常用到de匙ApplicationContextAware.实现ApplicationContextAwaredeBean,在Bean被初始后,将会被注入 Applicati
- linux shell ls脚本样例
annan211
linuxlinux ls源码linux 源码
#! /bin/sh -
#查找输入文件的路径
#在查找路径下寻找一个或多个原始文件或文件模式
# 查找路径由特定的环境变量所定义
#标准输出所产生的结果 通常是查找路径下找到的每个文件的第一个实体的完整路径
# 或是filename :not found 的标准错误输出。
#如果文件没有找到 则退出码为0
#否则 即为找不到的文件个数
#语法 pathfind [--
- List,Set,Map遍历方式 (收集的资源,值得看一下)
百合不是茶
listsetMap遍历方式
List特点:元素有放入顺序,元素可重复
Map特点:元素按键值对存储,无放入顺序
Set特点:元素无放入顺序,元素不可重复(注意:元素虽然无放入顺序,但是元素在set中的位置是有该元素的HashCode决定的,其位置其实是固定的)
List接口有三个实现类:LinkedList,ArrayList,Vector
LinkedList:底层基于链表实现,链表内存是散乱的,每一个元素存储本身
- 解决SimpleDateFormat的线程不安全问题的方法
bijian1013
javathread线程安全
在Java项目中,我们通常会自己写一个DateUtil类,处理日期和字符串的转换,如下所示:
public class DateUtil01 {
private SimpleDateFormat dateformat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
public void format(Date d
- http请求测试实例(采用fastjson解析)
bijian1013
http测试
在实际开发中,我们经常会去做http请求的开发,下面则是如何请求的单元测试小实例,仅供参考。
import java.util.HashMap;
import java.util.Map;
import org.apache.commons.httpclient.HttpClient;
import
- 【RPC框架Hessian三】Hessian 异常处理
bit1129
hessian
RPC异常处理概述
RPC异常处理指是,当客户端调用远端的服务,如果服务执行过程中发生异常,这个异常能否序列到客户端?
如果服务在执行过程中可能发生异常,那么在服务接口的声明中,就该声明该接口可能抛出的异常。
在Hessian中,服务器端发生异常,可以将异常信息从服务器端序列化到客户端,因为Exception本身是实现了Serializable的
- 【日志分析】日志分析工具
bit1129
日志分析
1. 网站日志实时分析工具 GoAccess
http://www.vpsee.com/2014/02/a-real-time-web-log-analyzer-goaccess/
2. 通过日志监控并收集 Java 应用程序性能数据(Perf4J)
http://www.ibm.com/developerworks/cn/java/j-lo-logforperf/
3.log.io
和
- nginx优化加强战斗力及遇到的坑解决
ronin47
nginx 优化
先说遇到个坑,第一个是负载问题,这个问题与架构有关,由于我设计架构多了两层,结果导致会话负载只转向一个。解决这样的问题思路有两个:一是改变负载策略,二是更改架构设计。
由于采用动静分离部署,而nginx又设计了静态,结果客户端去读nginx静态,访问量上来,页面加载很慢。解决:二者留其一。最好是保留apache服务器。
来以下优化:
- java-50-输入两棵二叉树A和B,判断树B是不是A的子结构
bylijinnan
java
思路来自:
http://zhedahht.blog.163.com/blog/static/25411174201011445550396/
import ljn.help.*;
public class HasSubtree {
/**Q50.
* 输入两棵二叉树A和B,判断树B是不是A的子结构。
例如,下图中的两棵树A和B,由于A中有一部分子树的结构和B是一
- mongoDB 备份与恢复
开窍的石头
mongDB备份与恢复
Mongodb导出与导入
1: 导入/导出可以操作的是本地的mongodb服务器,也可以是远程的.
所以,都有如下通用选项:
-h host 主机
--port port 端口
-u username 用户名
-p passwd 密码
2: mongoexport 导出json格式的文件
- [网络与通讯]椭圆轨道计算的一些问题
comsci
网络
如果按照中国古代农历的历法,现在应该是某个季节的开始,但是由于农历历法是3000年前的天文观测数据,如果按照现在的天文学记录来进行修正的话,这个季节已经过去一段时间了。。。。。
也就是说,还要再等3000年。才有机会了,太阳系的行星的椭圆轨道受到外来天体的干扰,轨道次序发生了变
- 软件专利如何申请
cuiyadll
软件专利申请
软件技术可以申请软件著作权以保护软件源代码,也可以申请发明专利以保护软件流程中的步骤执行方式。专利保护的是软件解决问题的思想,而软件著作权保护的是软件代码(即软件思想的表达形式)。例如,离线传送文件,那发明专利保护是如何实现离线传送文件。基于相同的软件思想,但实现离线传送的程序代码有千千万万种,每种代码都可以享有各自的软件著作权。申请一个软件发明专利的代理费大概需要5000-8000申请发明专利可
- Android学习笔记
darrenzhu
android
1.启动一个AVD
2.命令行运行adb shell可连接到AVD,这也就是命令行客户端
3.如何启动一个程序
am start -n package name/.activityName
am start -n com.example.helloworld/.MainActivity
启动Android设置工具的命令如下所示:
# am start -
- apache虚拟机配置,本地多域名访问本地网站
dcj3sjt126com
apache
现在假定你有两个目录,一个存在于 /htdocs/a,另一个存在于 /htdocs/b 。
现在你想要在本地测试的时候访问 www.freeman.com 对应的目录是 /xampp/htdocs/freeman ,访问 www.duchengjiu.com 对应的目录是 /htdocs/duchengjiu。
1、首先修改C盘WINDOWS\system32\drivers\etc目录下的
- yii2 restful web服务[速率限制]
dcj3sjt126com
PHPyii2
速率限制
为防止滥用,你应该考虑增加速率限制到您的API。 例如,您可以限制每个用户的API的使用是在10分钟内最多100次的API调用。 如果一个用户同一个时间段内太多的请求被接收, 将返回响应状态代码 429 (这意味着过多的请求)。
要启用速率限制, [[yii\web\User::identityClass|user identity class]] 应该实现 [[yii\filter
- Hadoop2.5.2安装——单机模式
eksliang
hadoophadoop单机部署
转载请出自出处:http://eksliang.iteye.com/blog/2185414 一、概述
Hadoop有三种模式 单机模式、伪分布模式和完全分布模式,这里先简单介绍单机模式 ,默认情况下,Hadoop被配置成一个非分布式模式,独立运行JAVA进程,适合开始做调试工作。
二、下载地址
Hadoop 网址http:
- LoadMoreListView+SwipeRefreshLayout(分页下拉)基本结构
gundumw100
android
一切为了快速迭代
import java.util.ArrayList;
import org.json.JSONObject;
import android.animation.ObjectAnimator;
import android.os.Bundle;
import android.support.v4.widget.SwipeRefreshLayo
- 三道简单的前端HTML/CSS题目
ini
htmlWeb前端css题目
使用CSS为多个网页进行相同风格的布局和外观设置时,为了方便对这些网页进行修改,最好使用( )。http://hovertree.com/shortanswer/bjae/7bd72acca3206862.htm
在HTML中加入<table style=”color:red; font-size:10pt”>,此为( )。http://hovertree.com/s
- overrided方法编译错误
kane_xie
override
问题描述:
在实现类中的某一或某几个Override方法发生编译错误如下:
Name clash: The method put(String) of type XXXServiceImpl has the same erasure as put(String) of type XXXService but does not override it
当去掉@Over
- Java中使用代理IP获取网址内容(防IP被封,做数据爬虫)
mcj8089
免费代理IP代理IP数据爬虫JAVA设置代理IP爬虫封IP
推荐两个代理IP网站:
1. 全网代理IP:http://proxy.goubanjia.com/
2. 敲代码免费IP:http://ip.qiaodm.com/
Java语言有两种方式使用代理IP访问网址并获取内容,
方式一,设置System系统属性
// 设置代理IP
System.getProper
- Nodejs Express 报错之 listen EADDRINUSE
qiaolevip
每天进步一点点学习永无止境nodejs纵观千象
当你启动 nodejs服务报错:
>node app
Express server listening on port 80
events.js:85
throw er; // Unhandled 'error' event
^
Error: listen EADDRINUSE
at exports._errnoException (
- C++中三种new的用法
_荆棘鸟_
C++new
转载自:http://news.ccidnet.com/art/32855/20100713/2114025_1.html
作者: mt
其一是new operator,也叫new表达式;其二是operator new,也叫new操作符。这两个英文名称起的也太绝了,很容易搞混,那就记中文名称吧。new表达式比较常见,也最常用,例如:
string* ps = new string("
- Ruby深入研究笔记1
wudixiaotie
Ruby
module是可以定义private方法的
module MTest
def aaa
puts "aaa"
private_method
end
private
def private_method
puts "this is private_method"
end
end