论文笔记《Accelerating Primal Solution Findings for Mixed Integer Programs Based on Solution Prediction》
目录
- 1. 引言
-
- 1.1 背景
- 1.2 文献综述
- 1.3 创新点
- 2. 求解框架
-
- 2.1 生成训练数据
- 2.2 GCN模型
-
- 2.2.1 产生三分图
- 2.2.2 MIP最优解预测1-算法过程
- 2.2.3 MIP最优解预测2-注意力机制
- 2.2.4 如何基于预测加速MIP求解
-
- 2.2.4.1 近似法
- 2.2.4.2 精确法
- 3. 应用
-
- 3.1 数据收集
- 3.2 算例
- 3.3 评估1-解预测结果
- 3.4 评估2-解质量比较
- 4. 总结
1. 引言
1.1 背景
- 疫情期间,面对收到影响的运输网络,如何规划路由与车线,利用有限的货车资源尽快将积压的包裹运达目的地,这是物流领域典型的组合优化问题,该问题可建模为混合整数规划问题 (Mixed Integer Programing, MIP),并利用求解器进行求解。
- 问题:
(1)快递网络规划问题通常规模很大,包含决策变量和约束条件众多,求解耗时,很难在短时间内求解完成并应用到线上。
(2)快递网络每天在运转,相似的组合优化问题也需要反复求解,当前尚无处理相似MIP问题的通用方法,每天计算时通常将其视为全新的求解任务
因此,如果能从历史求解中,采用机器学习的方法学习到类似MIP问题的结构特点,则有望大幅提高求解效率。
1.2 文献综述
本文的文献综述主要从两个角度阐述:
- 将ML(Machine Learning) 和OR(Operations Research,运筹学) 集成以解决CO(combinatorial optimization,组合优化) 问题的研究情况
- 将ML应用到MLP中,以提高MLP(Mixed Integer Programming,混合整数规划) 效果的研究情况
1.3 创新点
基于上述文献综述,引出本文不同于以往工作的两个方面:
- 以往研究解决CO问题的方法,都是基于特定的问题结构。本文提出的框架不限于特定的问题类型,而是可以应用到绝大多数的可以用MLP建模的CO问题,即适用范围更大。
- 以往研究为提高MLP求解效果,均采用人工特征,并且独立对每个变量进行预测。然而实际上,变量的解与目标函数、约束密切相关,因此我们提出三分图(a tripartite graph) 以表征MIP问题,在不需要人工介入的情况下,基于 graph embedding technique 以提取变量、约束、目标函数之间的相关性。
2. 求解框架
2.1 生成训练数据
针对组合优化问题,产生 p p p 个MIP实例 I = { I 1 , . . . , I p } \mathbb{I}=\left \{I_1,...,I_p\right \} I={I1,...,Ip},每个 I i I_i Ii 都存有变量特征、约束特征、边界特征,利用迭代近邻搜索方法(the iterated proximity search method)计算每个 I i I_i Ii 中的二元变量的label。
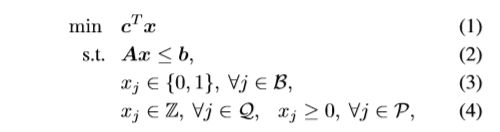
决策变量的索引集 U : = { 1 , . . . , n } \mathcal{U}:=\left \{1,...,n\right \} U:={1,...,n} ,被分割成 ( B , Q , P ) (\mathcal{B,Q,P}) (B,Q,P) ,其中:
- B \mathcal{B} B:二进制变量
- Q \mathcal{Q} Q:一般整数变量
- P \mathcal{P} P:连续变量
这样做的目的是预测 最优情况下 二元变量 x i , j ∈ B x_i, j\in \mathcal{B} xi,j∈B 取值为1或0的概率。
2.2 GCN模型
针对每个 I i I_i Ii 根据其MIP公式,产生一个三分图。基于已知的特征、label、三分图,训练GCN网络,以求得二元变量预测值。
2.2.1 产生三分图
三分图 G = { V , E } \mathcal{G=\left\{V,E\right \}} G={V,E}基础概念:
- V \mathcal{V} V 为点集, V \mathcal{V} V 可以划分为 X = { x i ∣ i = 1 , 2 , . . . , n } X=\left \{x_i|i=1,2,...,n\right \} X={xi∣i=1,2,...,n} Y = { y i ∣ i = 1 , 2 , . . . , n } Y=\left \{y_i|i=1,2,...,n\right \} Y={yi∣i=1,2,...,n} Z = { z i ∣ i = 1 , 2 , . . . , n } Z=\left \{z_i|i=1,2,...,n\right \} Z={zi∣i=1,2,...,n}
- E \mathcal{E} E 为边集

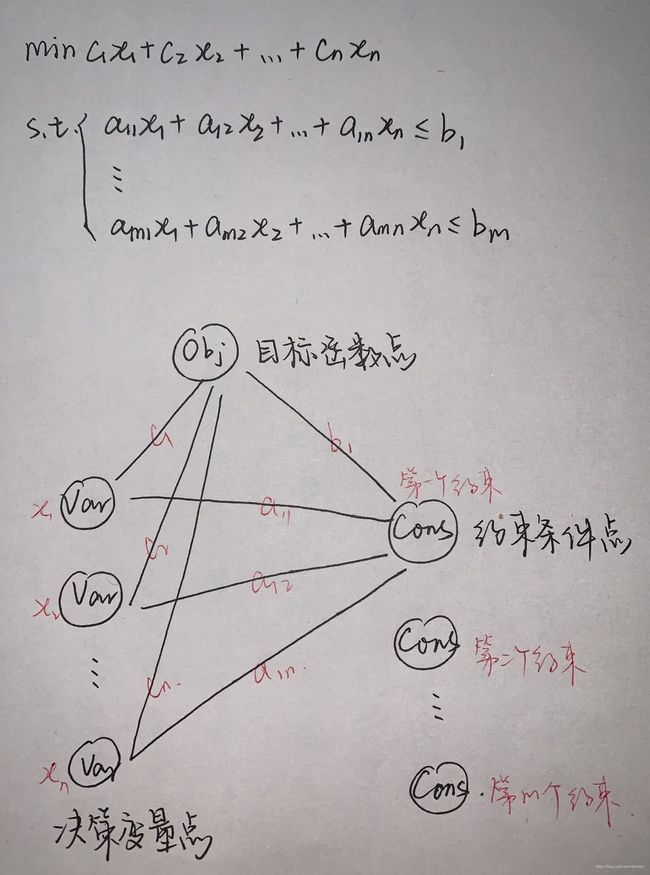
本文表示方法:
- 点1: 决策变量点 V V \mathcal{V}_V VV,每个点都是MIP实例 I I I 中的二元变量
- 点2: 约束条件点 V C \mathcal{V}_C VC,每个点都是MIP实例 I I I 中的一个约束
- 点3: 目标函数点 o o o
- 边1: 边 v ∼ c v\sim c v∼c,就是一条在 v ∈ V V v\in \mathcal{V}_V v∈VV 和 v ∈ V C v\in \mathcal{V}_C v∈VC 间的边,如果对应的决策变量 v v v 和约束条件 c c c 有非零值,则该边存在
- 边2: 边 v ∼ o v\sim o v∼o,就是对于每一个 v ∈ V V v\in \mathcal{V}_V v∈VV 都与目标函数存在一条边
- 边3: 边 c ∼ o c\sim o c∼o,就是对于每一个 c ∈ V C c\in \mathcal{V}_C c∈VC 都与目标函数存在一条边,该边是从对偶的角度说明
2.2.2 MIP最优解预测1-算法过程
- 经过 T T T 轮迭代和两层(带sigmoid)全连接层,得到预测值
- 三部图的节点更新如上图的高亮部分
- 该算法的思路是,让变量节点增量式的汇集来自邻居节点(对应于约束点和其他变量点)的信息。以上的转换只是提取了节点之间的连接关系,而忽略了详细的系数数值,为了增强表达能力,通过注意力机制导入来自系数的信息。具体信息流的转换(对应于上图的四个step),见下图。

2.2.3 MIP最优解预测2-注意力机制
-
三分图结构的显著特点就是节点和弧的异质性,而不是简单采用一个共享的线性变换。(即在三分图的每步更新里,都考虑了不同的变换方式,从而很好的反应了一种节点特征之于另一种节点的重要程度)
-
给定 T i T_i Ti 类型的点 i i i 和 T j T_j Tj 类型的点 j j j ,注意力系数就是表示了节点 i i i 对于其邻居 j j j 的重要程度,计算公式:

-
其中concat()中的三个h,分别代表了 i i i j j j 和边 ( i , j ) (i,j) (i,j)的embedding, W W W是两个类型节点的注意力权重矩阵
-
对于所有邻居节点 j j j 上的系数都要用softmax函数归一化
-
经过注意力机制处理,系数 A , b , c A,b,c A,b,c可以用于反应三分图中边的关系。(所以需要注意,上文手写图中的边的标注并不对,实际上还经过了注意力处理)
2.2.4 如何基于预测加速MIP求解
途径1:在MIP模型中加入local branching方法的割平面法,从而降低可行解的搜索空间。这种方法旨在识别可稳定预测的0-1决策变量,并将二分搜索树(分支定界树)引导到在难预测的变量上
途径2:保证全局最优,这其中有两个关键,如下。
2.2.4.1 近似法
- x j ^ , j ∈ B \hat{x_j},j\in B xj^,j∈B 表示决策变量的预测值
- S \mathcal{S} S 表示0-1变量索引集合的一个子集
- 割平面定义为:

- ϕ \phi ϕ 是控制可行解和预测最优解的最大距离的参数,根据索引集合 S \mathcal{S} S 进行割平面,而不是原来的拥有全部变量的 B \mathcal{B} B ,因为 S \mathcal{S} S 收集了不能稳定预测的点,因此只有那些高概率取0/1的点才会被纳入 S \mathcal{S} S 中(= = 这句话没太看懂,取0/1不是稳定预测的意思吗)
- ϕ = 0 \phi=0 ϕ=0 相当于将0-1变量以预测值固定在索引集合 S \mathcal{S} S 中。
2.2.4.2 精确法
从根节点创建两个子节点,在根节点分支后,再返回默认的求解方式执行分支定界树的过程

3. 应用
3.1 数据收集
- Features :理想的特征工程应该保证 (1)捕获足够的信息描述解决方案;(2)具有较低的计算复杂度,本文在分支定界树的根节点收集特征(该位置问题已被预先解决以消除冗余变量和约束),为每个实例收集了其变量特性、约束特性、边特性,最后将其分别归类为basic features, LP features, structure features.

- Labels :获得中/大型MIP问题的最优方案很耗时,这意味着我们只能获取可解的MIP问题,这限制了所提框架的应用。在难以获取最优解的情况下,我们提出了在解中识别稳定变量和不稳定变量的方法。
如何在解中识别稳定变量和不稳定变量?
该思路来源是,作者观察到在一系列不同可行解中,大多数二元变量解值保持不变,即:
给定MIP实例的 K K K 个解 { x ˉ 1 , . . . , x ˉ K } \left \{\bar{x}^1,...,\bar{x}^K\right \} {xˉ1,...,xˉK},
{ u n s t a b l e k 1 , k 2 ∈ { 1 , . . . , K } , x j k 1 ≠ x j k 2 s t a b l e o t h e r w i s e \left\{\begin{matrix} unstable & k_1,k_2\in \left \{1,...,K\right \},x_j^{k_1}\neq {x_j^{k_2}}\\ stable & otherwise \end{matrix}\right. {unstablestablek1,k2∈{1,...,K},xjk1=xjk2otherwise
为产生一系列实例解,作者采用the proximity search method,通过这种方法,稳定的二元变量的标签值即为其解值,不稳定的即从训练集中删掉。(这种标记方法的局限在于初始可行解难以获得)
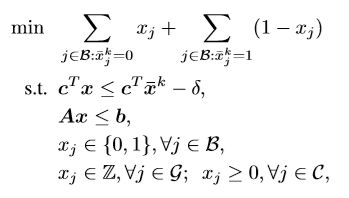
总结一下
关于label处理这块麻烦在于,大型的MIP问题(由于难解/不可解)我们不能直接得到全局最优解,于是作者去探寻局部最优解。通过the proximity search method方法的每次迭代,不断对二元变量的取值更新/丢弃。
3.2 算例
在目前性能最佳的开源MIP求解器SCIP中添加插件以实现数据采集与求解比较,GCN模型基于tensorflow搭建
作者采用了8类经典MIP问题模型生成算例,每类问题生成200个算例用于模型训练(140)、验证(20)、测试(40),在验证机上参数校准,在测试集评估精度。以下8类问题都是常见的组合优化问题,他们在模型架构和解结构上存在显著差异:
- 固定费用网络流问题 (Fixed Charge Network Flow, FCNF)
- 设施选址问题 (Capacitated Facility Location, CFL)
- 广义分配问题 (Generalized Assignment, GA)
- 最大独立集合问题(Maximal Independent Set, MIS)
- 多维背包问题 (Multidimensional Knapsack, MK)
- 集合覆盖问题 (Set Covering, SC)
- 旅行商问题 (Traveling Salesman Problem, TSP)
- 车辆路径问题 (Vehicle Routing Problem, VRP)
模型的性能取决于超参数 ϕ \phi ϕ 和 S \mathcal{S} S 的值,最优参数组合如下表:
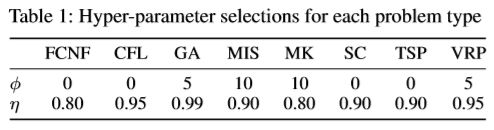
3.3 评估1-解预测结果
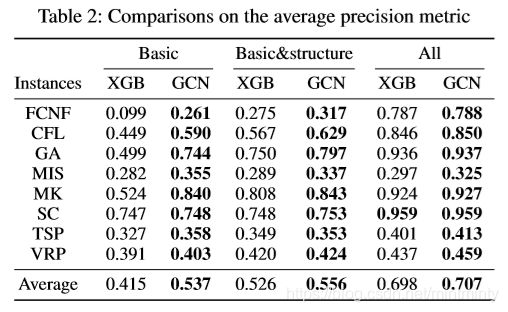
作者将GCN模型与 XGBoost 比较,使用平均查准率(average precision)度量精度:

精度如下:
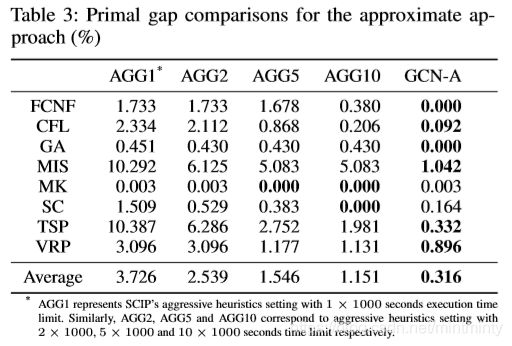
3.4 评估2-解质量比较
作者将新提出的方法与求解器默认方案的性能进行对比,评估指标为:
4. 总结
- 本文提出了有监督的预测框架,模型核心是三分图的表示方法,据此探索MIP方程结构的相关性极其局部最优。
- 通过对8类不同问题的大量实验评估,证明了GCN模型在预测精度方面的有效性和可泛化性。
- 存在问题:(1)该方法更适合二元变量密集型的问题,对于整数变量解值则求解困难。(2)如果问题没有局部最优,当全局视图(体现变量关系)无法从三分图反映的邻居节点信息中得到时,则该模型性能会下降。
参考文献/链接
【1】《Accelerating Primal Solution Findings for Mixed Integer Programs Based on Solution Prediction》
【2】疫情期间如何让快递送得更快?菜鸟网络AAAI论文用深度学习驱动MIP求解
【3】陆三清.三分图上的匹配及其算法和应用[D].上海:复旦大学,2003. DOI:10.7666/d.y556452.