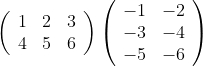深度学习中的编程语言Tensorflow
本章讲述的主要内容包括：预备知识；Tensorflow程序；多层神经网络；检查点、Tensordot、TF变量的初始化和TF图创建的简化；参考文献和补充阅读；习题。
2.1 预备知识
Tensorflow是谷歌开发的一种开源编程语言，旨在让深度学习程序编程变得更简单。我们首先从一个程序开始。
import tensorflow as tf
x = tf.constant("Hello World")
sess = tf.Session()
print(sess.run(x)) #will print out "Hello World"该程序是否看起来像Python代码呢？它的确就是Python代码。事实上，Tensorflow（后称TF）是一组函数集合，可以使用不同的编程语言来调用它。最完整的接口是Python的，这就是我们在上述程序中使用的。
要注意的是，TF函数与其说是执行一个程序，不如说是定义一个只有在调用run命令时才执行的计算，就像上面程序的最后一行一样。更准确地说，第3行中的TF函数Session创建了一个会话，与该会话相关联的是定义计算的图。像constant这样的命令会将元素添加到计算中。在本例中，元素只是一个常量数据项，其值是Python字符串“Hello World”。第4行代码显示TF计算与会话sess相关联的图中的x指向的TF变量。最终结果是——打印输出“Hello World”。
我们可以将上例最后一行替换为print(x)，进行对比。替换后输出
Tensor("Const:0", shape=(), dtype=string)关键是Python变量x并不绑定到字符串，而是绑定到Tensorflow计算图的一部分。只有当通过执行sess.run(x)来计算图的这一部分时，我们才能访问TF常量的值。
图2.1 TF中的placeholder
所以，在上面的代码中，x和sess是Python变量，可以根据我们的需要命名。import和print是Python函数，必须这样拼写，Python才能理解我们想要执行哪个函数。constant、Session和run是TF命令，拼写必须准确（包括Session中需要大写“S”)。此外，需要首先import tensorflow，这是固定的，我们在后文中不再提及。
在图2.1中的代码中，x仍是Python变量，其值是TF常量，在本例中是浮点数2.0。然后，z是Python变量，其值是TF placeholder。TF中的placeholder类似于编程语言函数中的变量。假设我们有以下Python代码。
x = 2.0
def sillyAdd(z):
return z+x
print(sillyAdd(3)) # Prints out 5.0
print(sillyAdd(16)) # Prints out 18.0这里z是sillyAdd参数的名称，当我们调用sillyAdd(3)中的函数时，z被它的值3所取代。TF程序的工作方式类似，不同之处在于给TF placeholder赋值的方式不同，如图2.1的第5行所示。
print(sess.run(comp,feed_dict={z:3.0}))这里的feed_dict是run的命名参数（因此它的名称必须拼写正确）。它接受Python字典这类值。在字典中，计算所需的每个placeholder都必须给定一个值。所以第一次sess.run打印输出为2.0和3.0的总和，第二次打印输出18.0。第三次调用sess.run时需要注意的是，如果计算不需要placeholder的值，则不必提供其值。另一方面，正如第4个打印输出语句后的注释所指出的，如果计算需要一个值，但没有提供该值，就会出现错误。
Tensorflow的命名源于其基本数据结构是张量型（tensor）多维数组。大约有十五种或更多张量类型。当我们定义上面的placeholder z时，我们给出了它的类型为float32。除了它的类型，张量也有形状。想象一个2×3的矩阵，它的形状就是[2, 3]。长度为4的向量形状为[4]，它不同于形状为[1,4]的1×4矩阵，或者形状为[4,1]的4×1矩阵。一个3×17×6的数组形状为[3,17,6]。他们都是张量。标量（即数字）的形状是null，也属于张量。此外，请注意张量不像线性代数，它不需要区分行向量和列向量。有些张量的形状只有一个分量，例如[5]。我们如何在纸上画出这些张量对数学来说无关紧要。我们对数组张量进行图示时，总是遵循第零个维度垂直绘制，第一个维度水平绘制的规则。但这是我们为保持一致进行的限制。请注意，张量维数和下标都是从零开始的。
回到我们对placeholder的讨论：大多数placeholder不是前述例子中的简单标量，而是多维张量。2.2节从一个简单的用于Mnist数字识别的Tensorflow程序开始。其中将一张图片输入TF代码，并运行神经网络前向传递，以获得网络对数字的预测。此外，在训练阶段，运行反向传递并修改程序的参数。为了给程序传入图片输入，我们定义了一个placeholder。它是float32型，形状为[ 28,28]，或者是[784]，这取决于我们给它的是一个二维Python列表还是一维Python列表。例如，
img=tf.placeholder(tf.float32,shape=[28,28])请注意，shape是placeholder函数的命名参数。
在深入讨论真正的程序之前，我们先看TF数据结构。如前所述，神经网络模型由它们的参数和程序的结构来定义——如何将参数与输入值组合以产生答案。通常我们随机初始化参数（例如，连接输入图像和答案logit的权重w），神经网络会修改参数以在训练数据上最小化损失。创建TF参数有三个阶段。首先，用初始值创建张量，然后将张量转换为Variable（TF对参数的称谓），然后初始化变量或者说参数。我们来创建图1.11中前馈Mnist伪代码所需的参数。首先是偏置项b，然后是权重W。
bt = tf.random_normal([10], stddev=.1)
b = tf.Variable(bt)
W = tf.Variable(tf.random_normal([784,10],stddev=.1))
sess=tf.Session()
sess.run(tf.global_variables_initializer())
print(sess.run(b))第1行添加了创建形状为[10]的张量的指令，张量的十个值是从标准偏差为0.1的正态分布生成的随机数。正态分布，也称为高斯分布，是常见的钟形曲线。从正态分布中选取的数字将以平均值（µ）为中心，它们离平均值的距离由标准偏差（σ）决定。更具体地说，大约68 %的值处在平均值的一个标准偏差范围内，超出这个范围的数字出现概率会大大降低。
上面代码的第2行输入为bt，并添加了一段TF图，该图创建了一个与bt具有相同形状和值的变量。一旦我们创建了变量，我们就很少需要原始张量，所以通常会同时进行上述两个事件而不保存张量指针，就像创建参数W的第3行一样。在使用b或W之前，我们需要在创建的会话中对它们进行初始化，这是第5行的工作。第6行是打印输出结果（结果如下，每次都会不同）。
[-0.05206999 0.08943175 -0.09178174 -0.13757218 0.15039739
0.05112269 -0.02723283 -0.02022207 0.12535755 -0.12932496]如果我们颠倒了最后两行的顺序，当尝试打印b所指的变量时，就会收到一条错误消息。
因此，在TF程序中，我们创建变量来存储模型参数。最初，参数的值是不含信息的，通常是标准偏差很小的随机值。根据之前的讨论，梯度下降的反向传递修改了它们。一旦被修改，sess指向的会话将保留新值，并在下次运行会话时使用它们。
2.2 TF程序
图2.2是前馈神经网络Mnist程序的TF版本，它比较完整，应该可以运行。这里隐藏的关键元素是代码mnist.train.next_batch，它处理Mnist数据中的读取细节。先大体看一看图2.2，请注意虚线之前的所有内容都与设置TF计算图有关；虚线之后首先使用图来训练参数，然后运行程序来查看测试数据的准确性。现在我们逐行解读这个程序。
首先，是import tensorflow和Mnist数据的读取代码，然后在第5行和第6行定义了两组参数，这和刚才讨论的TF变量定义有一点小变化。接下来，我们为输入神经网络的数据定义placeholder。首先，在第8行，定义图像数据的placeholder，这是一个形状为[batchSz,784]的张量。在讨论线性代数为什么是表示神经网络计算的好方法时（1.5节），我们注意到，同时处理几个样本时，我们的计算速度会加快，而且，这与随机梯度下降中的批处理概念非常吻合。在图2.2中，我们可以看到这一点在TF中如何实现。也就是说，图片的placeholder不是一行784个像素，而是100行（这取于batchSz的值）。程序第9行与之类似，我们的程序一次性给出100张图片的预测。
图2.2 Mnist的前馈神经网络的Tensorflow代码
在第9行中还需注意一点。我们用包含10个数字的向量表示一个答案，所有数字值都为零，除了第a个，其中a是该图像对应的正确数字。例如，第1章中的数字7的图片（图1.1），正确答案的对应表示是( 0,0,0,0,0,0,0,1,0,0 )。这种形式的向量被称为独热（one-hot）向量，因为它们具有仅选择一个值作为激活值的特性。
截至第9行是程序的参数定义和输入，下面的代码是完成图中的计算。其中第11行开始显示TF用于神经网络计算的强大能力。它定义了模型的神经网络前向传递，将（一个批大小的）图片输入线性单元（由W和b定义），然后对所有结果应用softmax函数以得到一个概率向量。
我们建议在查看类似代码时，首先检查所涉及的张量的形状，以确保它们是合理的。这里隐藏最深的计算是矩阵乘法matmul，即输入图片[100,784]乘以W[784, 10]得到一个形状为[100,10]的矩阵。接着我们将偏置与矩阵相加，得到一个形状为[100,10]的矩阵，这是100张图片的批中的10个logit。然后，将结果通过softmax函数处理，最后会得到图片对应的[100, 10]大小的标签概率分配矩阵。
第12行并行计算100个样本的平均交叉熵损失。我们从里到外进行讲解。tf.log(x)返回一个张量，使得x的每个元素都被它的自然对数代替。图2.3展示了tf.log如何进行批操作，批大小为3，批中每个向量都包含5个概率分布。
图2.3 tf.log的批操作
接下来，ans * tf.log(prbs)中的标准乘法符号“*”代表两个张量的逐元素相乘。图2.4显示了在批运算中，每个标签的独热向量与负自然对数矩阵的逐元素相乘如何进行。结果中的每一行，除了正确答案概率对应的负对数之外，所有内容都被清零。
图2.4 答案乘概率的负对数的计算
此时，为了获得每张图片的交叉熵，我们只需要对数组中的所有值求和。求和的第一步操作是
tf.reduce_sum( A, reduction_indices = [ 1 ] )它将A的各行相加，如图2.5所示。这里的一个关键部分是
reduction_indices = [ 1 ]在我们之前对张量的介绍中，提到了张量的维数是从零开始的。reduce_sum可以对列求和，默认情况下，reduction_indices=[0]，或者，如本例中，对行求和，reduction_indices=[1]。这将生成一个[100,1]的数组，每行中只有正确概率的对数作为唯一的条目。图2.5设批大小为3，并假设有5个类，而不是10个。作为交叉熵计算的最后一个部分，图2.2中第12行reduce_mean对所有列求和（同样reduction_indices是默认值），并返回平均值（1.1左右）。
图2.5 根据reduction_indices为[1]进行tf.reduce_sum计算
最后，我们可以转到图2.2中的第14行，在此TF真正展示了它的优点，这一行就实现了整个反向传递所需的全部内容。
tf.train.GradientDescentOptimizer(0.5).minimize(xEnt)即，使用梯度下降来计算权重变化，并最小化由第12行和第13行定义的交叉熵损失函数。该行还指定了0.5的学习率。我们不必担心计算导数或其他元素，因为如果你在TF中定义了前向计算和损失，那么TF编译器会知道如何计算必要的导数，并按照正确的顺序将它们串在一起对权重进行修改。我们可以通过选择不同的学习率来修改这个函数调用，或者，如果我们使用不同的损失函数，可以用另一个TF计算的元素替换xEnt。
当然，TF基于前向传递导出反向传递的能力是有限的。再强调一次，只有当所有前向传递计算都用TF函数完成时，它才能做到这一点。对于像我们这样的初学者来说，这并不是太大的限制，因为TF有各种各样的内置操作，它知道如何进行区分和连接。
第15行和第16行代码计算模型的accuracy（精度）。精度是模型计算正确答案的数量除以处理的图片数量。首先，关注标准数学函数argmax，如
，它返回让f(x)最大化的x值。在这里，我们使用的tf.argmax(prbs, 1)有两个参数：第一个是张量，我们从中取argmax；第二个是取argmax的张量轴。张量轴的作用与我们用于reduce_sum的命名参数类似——它帮助我们在张量的不同轴上求和。举例来说，如果张量是( ( 0,2,4 ), ( 4,0,3 ) )，并且使用轴0（默认值），我们会得到( 1,0,0 )。我们先比较0和4，由于4更大，所以返回1。然后我们比较2和0，由于2更大，所以返回0。如果我们使用轴1，我们会返回( 2,0 )。第15行有一个批大小logit的数组。argmax函数返回批大小的最大logit所在位置的数组。接下来，我们应用tf.equal将最大logit与正确答案进行比较。tf.equal返回一个批向量的布尔值（如果它们相等，则为True），tf.cast(tensor,tf.float32)将该向量转换为浮点数，以便tf.reduce_mean将它们相加，得到正确率的百分比。请注意不要将布尔值转换成整数，因为取平均值时，它会返回一个整数，在这种情况下，该整数将始终为零。
定义了会话（第18行）并初始化参数值（第19行）之后，我们可以训练模型（第21行至第23行）。在这三行代码中，我们使用从TF Mnist库中获得的代码每次提取100张图片及其答案，然后通过调用sess.run在训练的计算图上运行程序。当这个循环结束时，我们共训练了1,000次，每次迭代有100张图片，或者说总共训练了100,000张测试图片。我的Mac Pro电脑具有四核处理器，完成这轮循环大约需要5秒（第一次将内容放入缓存中会花费较长时间）。提到“四核处理器”是因为TF会查看可用的计算能力，在没有指导时也能很好地使用电脑的计算能力。
你可能注意到了，第21行到第23行有一点奇怪——我们从来没有明确提到过要进行前向传递，而TF根据计算图（Computation graph）计算出了这一点。从GradientDescentOptimizer中，TF知道自己需要执行xEnt所需的计算（第12行），这需要计算prbs，而该计算又指向了第11行的前向传递计算。
最后，第25行到第29行计算测试数据的正确率（91%或92%）。首先，通过浏览计算图的组织结构可以发现，accuracy计算最终需要的是在前向传递中计算prbs，而不是反向传递的训练。因此，为了更好地测试数据，不对权重进行修改。
第1章中提到，在训练模型时打印输出错误率是良好的调试实践。一般来说，错误率会下降。为此，我们将第23行改为
acc,ignore= sess.run([accuracy,train],
feed_dict={img: imgs, ans: anss})这里的语法是用于组合计算的普通Python语言。计算的第一个值（accuracy的值）分配给变量acc，计算的第二个值分配给ignore。Python的习惯做法是用下划线符号( _ )代替ignore，当语法要求变量接受一个值，但我们不需要记住它时，Python会使用下划线符号。当然，我们还需要添加一个命令来打印输出acc的值。
我们提到这一点是为了帮助读者避免一个常见的错误——无视第23行，反而自己新增了第23.5行（我和一些刚入门的学生都犯过这个错误）。
acc= sess.run(accuracy, feed_dict={img: imgs, ans: anss})这种做法效率较低，因为TF在这种情况下需要进行两次前向传递，一次是在要进行训练时，另一次是在求accuracy时。更重要的是，第一次调用会修改权重，从而更有可能为该图片预测正确的标签。如果在此之后计算accuracy，程序的性能就会有所夸大。当我们调用一次sess.run，但同时求两个值时，就不会发生这种情况。
2.3 多层神经网络
我们设计的程序，如第1章中的伪代码和第2章的TF代码，都是单层神经网络，只有一层线性单元。问题来了，多层线性单元表现会更好吗？早期神经网络研究人员认为答案是“否”，下面解释为什么。线性单元可以被看作线性代数矩阵，即我们看到一层前馈神经网络只是计算y = XW。在我们的Mnist模型中，为了将784个像素值转换成10个logit值，W的形状设置为[ 784,10 ]，并增加额外的权重来替换偏置项。假设我们又添加了一层线性单元U，其形状为[ 784,784 ]，输出到层V中，层V和W形状一样，是[ 784,10 ]，
（2.1）
（2.2）
其中第2行遵循矩阵乘法的结合律。这里的重点是，使用两层神经网络U和V相乘得到的能力，都可以由W= UV的单层神经网络得到。
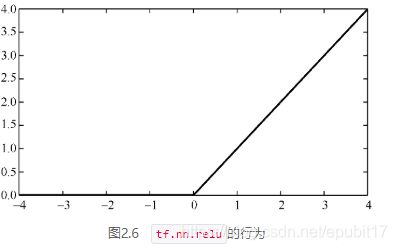
有一个简单的解决方案——在层与层之间添加一些非线性计算。最常用的一种是tf.nn.relu（或ρ），修正线性单元（rectified linear unit，以下简称relu），定义为
（2.3）
函数图像如图2.6所示。
图2.6 tf.nn.relu的行为
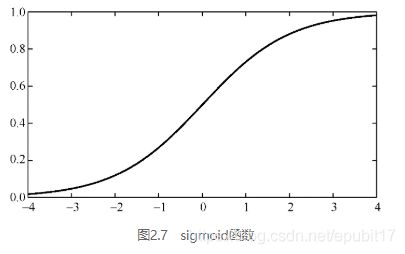
在深度学习中，置于各层之间的非线性函数称为激活函数（activation function）。除了常用的relu以外，其他一些激活函数也活跃于程序中，例如sigmoid函数，定义为
（2.4）
函数图像如图2.7所示。在所有情况下，激活函数都分别应用于张量参数中的各个实数。例如，ρ([1,17, −3 ] ) = [ 1,17,0]。
图2.7 sigmoid函数
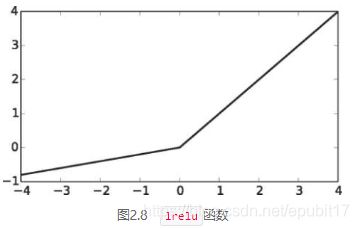
在发现relu这种有效简单的非线性函数前，sigmoid函数非常受欢迎。但是sigmoid可以输出的值范围非常有限，只限于从0到1，而relu输出的值可以从0到无穷大。当我们进行反向传递计算梯度找出参数如何影响损失时，这一点非常关键。反向传播时，若使用sigmoid函数会使梯度为0——这个过程被称为梯度消失（vanishing gradient）问题。更简单的激活函数会极大改善这个问题，鉴于此，tf.nn.lrelu——带泄露修正线性单元（leaky relu）——使用非常频繁，因为它比relu可输出的值范围更大，如图2.8所示。
图2.8 lrelu函数
将多层神经网络放在一起，得出新模型。
（2.5）
其中σ是softmax函数，U和V是第一层和第二层线性单元的权重，bu和bv是它们的偏置。
现在我们在TF中进行实现。我们将图2.2第5行和第6行中的W和b的定义替换为图2.9第1行到第4行的层U和V，图2.2第11行prbs的计算替换为图2.9的第5行至第7行。这些替换将原代码转换成多层神经网络。此外，考虑到参数数量更多了，我们将学习率降低为
。旧程序在100,000张图片上训练后得出的精度稳定在92%左右，新程序在100,000张图片上的精度会达到94%左右。另外，如果我们增加训练图片的数量，测试集的性能会一直提高到大约97%。注意，这个代码和没有非线性函数的代码之间的唯一区别是第6行。如果我们删除它，精度会下降到大约92%。这足以让你相信数学的力量！
图2.9 用于多层神经网络识别数字的TF图构造代码
还有一点需要注意，在具有数组参数W的单层神经网络中，W的形状由输入数量（784）和输出数量（10）固定。对于两层线性单元，我们则可以自由地选择隐藏层大小（hidden size）。所以U是输入大小×隐藏层大小，V是隐藏层大小×输出大小。在图2.9中，我们只是将隐藏层大小设定为784，与输入大小相同，但是这并不是必须的。通常，加大隐藏层会提高性能，但也会有极限。
2.4 其他方面
在本节中，我们将介绍TF的其他方面——有助于完成本书其余部分中提出的编程任务的知识（例如，检查点），或者是在接下来的章节中会用到的知识。
2.4.1 检查点
在TF计算中添加检查点（checkpoint）通常很有用——将张量保存下来，以便可以在下一次恢复计算，或者在不同的程序中重新使用该张量。在TF中，我们通过创建和使用saver对象来实现这一点。
saveOb= tf.train.Saver()如前节所述，saveOb是Python变量，你可以选择名称。在使用对象之前，可以在任意时间创建它，但是由于后文提到的原因，在初始化变量（调用global_variable_initialize）之前创建这个对象更为合理。然后在每n轮训练后，保存所有变量的当前值。
saveOb.save(sess, "mylatest.ckpt")save函数有两个参数：要保存的会话以及文件名和位置。在上述语句的情况下，保存的目录与Python程序所在目录相同。如果这个参数是tmp/model.checkpt，它就会出现在tmp子目录中。
调用save函数创建了四个文件。最小的文件，名为checkpoint，是一个Ascii文件，指定了在该目录存储检查点的一些高级细节。名称checkpoint是固定的，如果你将某个文件命名为“checkpoint”，它将被覆盖。其他三个文件名会根据你提供的字符串来定义。在本例中，它们被命名为
mylatest.ckpt.data-00000-of-00001
mylatest.ckpt.index
mylatest.chpt.meta第一个文件保存了参数值。另外两个文件包含TF导入这些值时使用的元信息（稍后将进行描述）。如果你的程序反复调用save，这些文件每次都会被覆盖。
接下来如果我们想在已经训练过的同一个神经网络模型上做进一步的训练，最简单的操作就是修改原来的训练程序。你保留了saver对象，现在我们想用保存的值初始化所有TF变量。因此，我们通常会移除global_variable_initialize，通过调用saver对象的“restore”方法来替换global_variable_initialize。
saveOb.restore(sess, "mylatest.ckpt")下次调用训练程序时，它会恢复训练，TF变量自动设置为上次训练中保存的值，其他一切都没有改变。因此，如果在训练代码时，打印轮数及其对应损失，它会从1开始打印轮数，除非你修改了代码。当然，如果你想调整打印输出，或者想让程序更加优雅，你可以修改代码，但是在这里编写更好的Python代码不是我们要关心的。
2.4.2 tensordot
tensordot函数是TF中矩阵乘法在张量上的推广。我们对标准矩阵乘法非常熟悉，即前一章中的matmul。当A和B具有相同的维度个数n，A的最后一个维度与B的倒数第二个维度大小相同，并且前n−2个维度相同时，我们可以调用函数tf.matmul( A,B )。因此，如果A的维度是[ 2,3,4 ]，B的维度是[ 2,4,6 ]，那么乘积维度是[ 2,3,6 ]。矩阵乘法可以看作重复的点积。例如，矩阵乘法
（2.6）
可以通过将向量( 1,2,3)和( −1, −3, −5 )进行点积，并将答案放在结果矩阵的左上角位置来实现。以这种方式继续运算，第i行与第j列的点积，即为第i行第j列的结果。因此，设A是式（2.6）的第一个矩阵，B是第二个，这个计算也可以表示为
tf.tensordot(A, B, [[ 1 ], [ 0 ]])前两个参数是进行运算的张量，第三个参数是一个双元素列表：第一个元素是来自第一个参数需要进行点积的维度列表，第二个元素是第二个参数的相应维度列表。这个双元素列表指导tensordot获取这两个维度的点积。当然，如果我们要取它们的点积，指定的维度大小必须相等。由于垂直绘制第0个维度，水平绘制第1个维度，这意味着取A的每一行和B的每一列的点积。tensordot的结果按照从左到右取维度，先取A的剩余的维度后取B的。也就是说，在本例中，输入张量维度为[2,3]和[3,2]，在点积中指定的两个维度“消失”了（维度1和维度0），以得到维度为[2,2]的结果。
图2.10给出的例子更为复杂，导致matmul无法在一条指令中处理它。我们将此图从第5章拿过来作为例子（第5章中会解释变量的名字含义），但在本章中，我们只是通过它观察tensordot在做什么。不看数字，只看tensordot函数调用中的第三个参数 [ [ 1 ], [ 0 ] ]，即取encOut的1维和wAT的0维的点积。因为他们大小都为4，所以这是可行的。也就是说，我们取两个维度分别为[2,4,4]和[4,3]的张量的点积（斜体数字是进行点积的维度）。由于这些维度在点积之后消失，因此得到的张量具有维度[ 2,4,3 ]，当我们在例子最后打印输出时，该张量维度是正确的。简单地说一下实际的计算，我们对两个张量显示为列的维度取点积，即，第一个点积是对[ 1,1,1,−1 ]和[ 0.6,0.2,0.1,0.1 ]进行计算，得出的0.8作为结果张量中的第一个数值。
图2.10 tensordot实例
最后，tensordot不限于在每个张量中进行一维的点积。如果A的维度是[ 2,4,4 ]，而B的维度是[ 4,4 ]，那么运算tensordot ( A,B,[ [ 1,2 ],[ 0,1 ] ])会得到维度[ 2 ]的张量。
2.4.3 TF变量的初始化
在1.4节中，我们说过，随机初始化神经网络参数（即TF变量）且保证其接近于0是个很好的实践。在第一个TF程序（图2.9）中，我们使用如下命令实现这一操作。
b = tf.Variable(tf.random normal([10], stddev=.1))其中，我们假设0.1的标准偏差足够“接近0”。
然而，关于标准差的选择自有一套理论和实践体系。这里我们给出了一个名为“Xavier初始化”的规则，它通常用于在随机初始化变量时设置标准差。设ni为层的输入数，no为层的输出数，对于图2.9中的变量W，ni= 784，即像素的数量；no = 10，即备选分类的数量。针对Xavier初始化，设置标准差σ为
（2.7）
例如，对于W将值784和10代入，标准差σ约为0.0502，四舍五入为0.1。通常，推荐将标准差设在0.3（10×10层）和0.03（1,000×1,000层）之间。输入和输出值越多，标准差越低。
Xavier初始化最初是为了与sigmoid激活函数一起使用而提出的（见图2.7）。如前所述，当x远低于−2或高于+2时，σ(x)对x几乎毫无反应。也就是说，如果输入sigmoid函数的值太高或太低，它们的变化可能对损失几乎没有影响。进行反向传递时，如果损失的变化被sigmoid函数抵消，那么它不会影响输入sigmoid函数的参数。实际上，我们希望一层的输入和输出之间的比率方差（variance）大约为1。这里我们使用技术意义上的方差：数值随机变量 值和其均值之间平方差的期望值。此外，随机变量X的期望值（expected value）（用E[X]表示）是其可能取值的概率平均值。
![E\left[ X \right]=\sum\limits_{x}{p(X=x)}\times x](http://img.e-com-net.com/image/info8/fc396c5506584efdbef2d833f043f8d9.gif){kind=small}
（2.8）
以六面骰子为例，滚动一个六面骰子的期望值计算如下：
![E\left[ R \right]=\frac{1}{6}\times 1+\frac{1}{6}\times 2+\frac{1}{6}\times 3+\frac{1}{6}\times 4+\frac{1}{6}\times 5+\frac{1}{6}\times 6=3.5](http://img.e-com-net.com/image/info8/7caf90fce4874fe3ba007ada81c5c6c7.gif){kind=small}
（2.9）
因此，我们希望将输入方差与输出方差之比保持在1左右，该层不会由于sigmoid函数而对信号过度衰减。这限制了我们初始化的方式。我们传达了一个原始事实（你可以查看推导过程），对于一个权重矩阵为W的线性单元，前向传递的方差(Vf)和反向传递的方差(Vb)分别为
（2.10）
（2.11）
其中σ是W权重的标准偏差。（单个高斯的方差是(σ2)，所以这说得通。）如果我们把Vf和Vb都设为零，然后求解σ可得
（2.12）
（2.13）
除非输入的基数与输出的基数相同，否则这没有解。由于通常情况并非如此，所以我们在这两个值之间取一个“平均值”，得出Xavier规则。
（2.14）
对于其他激活函数，也有等价的方程。随着relu和其他激活函数的出现，而这些激活函数不像sigmoid那样容易饱和，因此这个问题不再像以前那么重要了。尽管如此，Xavier规则确实提供了很好地设置标准偏差的方法，它的TF程序版本和其他语言相关版本都十分常用。
2.4.4 TF图创建的简化
回顾图2.9，可以看到需要7行代码来描述两层前馈网络。可以想想看，如果在没有TF的情况下，我们用Python编程描述这样少的内容会需要多少代码。如果我们用图2.9的方式创建一个8层网络——在本书结尾你需要完成这个任务——将需要大约24行代码。
TF有一组方便的函数，即layers模块，可以更紧凑地对常见的分层情形进行编码。在这里我们介绍
tf.contrib.layers.fully_connected.如果一层的所有单元都连接到下一层的所有单元，则该层称为完全连接。我们在前两章中使用的层都是完全连接的，因此之前没有将它们和其他网络进行区分。定义这样一个层，我们会做以下工作：（a）创建权重W；（b）创建偏置b；（c）进行矩阵乘法并加和偏置；（d）应用激活函数。假设我们已经执行了import tensorflow.contrib.layers as layers，可以用下面的一行代码来完成定义工作。
layerOut=layers.fully_connected(layerIn,outSz,activeFn)上述调用创建了一个用Xavier方法初始化的矩阵和一个以零初始化的偏置向量。它返回layerIn乘矩阵再加上偏置的结果，并将activeFn指定的激活函数应用于该结果。如果你没有指定激活函数，它会使用relu；如果你指定None作为激活函数，则不使用激活函数。
使用fully_connected，我们可以将图2.9中的7行代码写为
L1Output=layers.fully_connected(img,756)
prbs=layers.fully_connected(L1Output,10,tf.nn.softmax)请注意，我们指定tf.nn.softmax作为第二层的激活函数，以作用于第二层的输出。
当然，如果我们有一个100层的神经网络，写出100个fully_connected的调用是非常冗长乏味的。幸运的是，我们可以使用Python或者TF API来定义我们的网络。举一个想象中的例子，假设我们想要创建100个隐藏层，每一层比前一层小1，其中第一层的大小是一个系统参数。我们可以写出
outpt = input
for i in range(100):
outpt = layers.fully_connected(outpt, sysParam - i)}这个例子很傻，但反映了很重要的一点：TF图的部分可以像列表或字典一样在Python中传递和操作。
2.5 参考文献和补充阅读
Tensorflow起源于谷歌内部项目——谷歌大脑，这个项目由两名谷歌的研究人员Jeff Dean和Greg Corrado以及斯坦福大学教授Andrew Ng发起。开始时，该项目被称为“Distbelief”，当它的应用超越了初始项目时，谷歌正式接管了进一步的开发，并聘请了多伦多大学的Geoffrey Hinton，我们在第1章中提到了他对深度学习的开创性贡献。
Xavier初始化来源于Xavier Glorot的名字。他以第一作者的身份撰写了介绍Xavier初始化的文章[GB10]。
如今，Tensorflow只是深度学习的编程语言之一（参见文献[Var17]）。就用户数量而言，Tensorflow是迄今为止最受欢迎的语言。第二位是Keras，一种建立在Tensorflow之上的高级语言。第三位是Caffe，最早是由加州大学伯克利分校开发的。Facebook现在支持Caffe的开源版本Caffe2。Pytorch是Torch的Python接口，它在深度学习自然语言处理社群十分受欢迎。
2.6 习题
练习2.1 如果在图2.5中，我们计算tf.reduce_sum(A)，其中A是图左侧的数组，结果会是怎样的？
练习2.2 从图2.2中取出第14行并将其插入第22行和第23行之间（循环如下），会产生什么问题？
for i in range(1000):
imgs, anss = mnist.train.next_batch(batchSz)
train = tf.train.GradientDescentOptimizer(0.5).minimize(xEnt)
sess.run(train, feed_dict={img: imgs, ans: anss})练习2.3 下面是图2.2中第21行到第23行代码的另一个变体，它有没有问题？如果有问题，是什么问题？
for i in range(1000):
img, anss= mnist.test.next_batch(batchSz)
sumAcc+=sess.run(accuracy, feed_dict={img:img, ans:anss})练习2.4 在图2.10中，以下操作输出的张量形状是什么？
tensordot(wAT, encOut, [[0],[1]])并给出解释。
练习2.5 展开计算过程，确认图2.10的例子最后打印输出的张量中第一个数字( 0.8 )是正确的（精确到三位小数）。
练习2.6 假设input的形状为[50,10]，以下代码创建了多少TF变量？
O1 = layers.fully connected(input, 20, tf.sigmoid)创建的矩阵中变量的标准偏差是多少？
本文摘自最新上架的《深度学习导论》
- 人工智能深度学习经典入门书
- 基于TensorFlow和Python，美国常青藤名校经典教材
- 理论与实战结合的良好典范，附带习题和答案
编辑推荐：
1.国内知识图谱界领军人物、文因互联CEO鲍捷作序。国内外产业界和学术界大咖鼎力推荐
2.本书编写简明扼要，是美国常青藤名校布朗大学的教材。本书的每一章都包括了一个编程项目和一些书面练习，并附上了参考资料，可供读者进一步阅读。
3.人工智能经典入门书，基于Tensorflow编写，以项目为导向，通过一系列的编程任务，向读者介绍了热门的人工智能应用，包括计算机视觉、自然语言处理和强化学习等。
4.做中学。作者在前言中写道：“对我而言，学习计算机科学的最好方法，就是坐下来写程序。”本书正是采用了这种方法。