gWQS包的使用
介绍
加权量化和(WQS)回归是一种统计模型,用于环境暴露、表观/基因组学和代谢组学研究等常见的高维数据集的多变量回归。该模型构建了一个加权指数,估计所有预测变量对结果的混合效应,然后可以在带有相关协变量的回归模型中使用,以检验该指数与因变量或结果的关联。然后,每个单独的预测因素对整体指数效应的贡献可以通过模型分配给每个变量的权重的相对强度来评估。
gWQS包将WQS回归扩展到具有连续和分类结果的应用中,并实现了随机子集WQS和重复保持WQS。在实践中,分析的主要产出将是参数估计和预测变量的总体指数效应的显著性检验,以及分配给每个预测变量的估计权重,它确定了每个变量对WQS指数和结果变量之间关系的相关贡献。
关于WQS回归及其扩展的其他理论背景,见下面提供的参考资料。
gWQS包的使用
gWQS包的主要功能是gwqs和gwqsrh。第一个函数将WQS回归扩展到连续、分类和计数结果的应用中,并包括允许应用WQS的随机子集实现的选项rs;第二个函数依赖于gwqs函数,并将该方法扩展到重复保持验证程序。在这个介绍中,我们将只展示WQS在连续结果中的应用。我们创建了wqs_data数据集(安装并加载软件包后即可使用)来展示如何使用这个函数。这些数据反映了从参加NHANES研究(2001-2002年)的受试者中测得的34种多氯联苯暴露和25种邻苯二甲酸盐生物标志物的分布中模拟的59种暴露浓度。此外,还模拟了8个结果指标,对预测因子采用不同的分布和固定的β系数。特别是y和yLBX被模拟为正态分布,ybin和ybinLBX为二项分布,ymultinom和ymultinomLBX为多项分布,ycount和ycountLBX为泊松分布。性别变量也被模拟,以便在模型中调整一个协变量。因此,这个数据集可以用来测试gWQS软件包,分析模拟的化学品对不同结果的混合效应,并对协变量进行调整。
例一
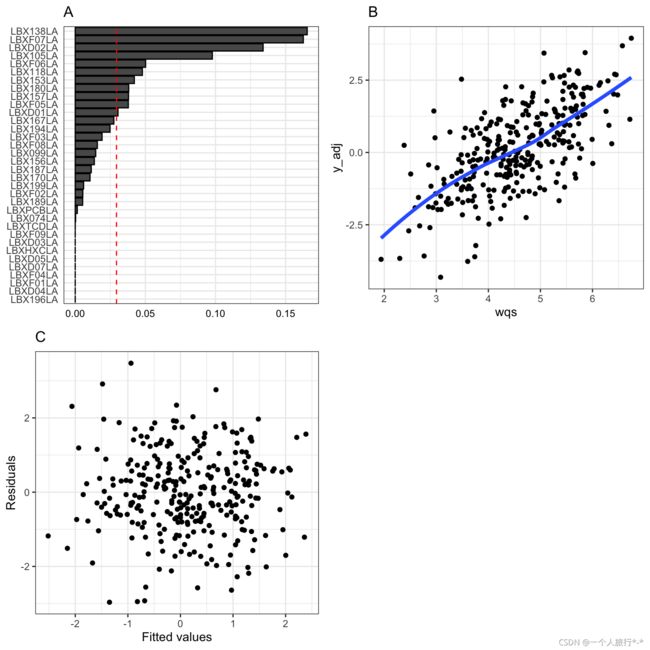
下面的脚本使用函数gwqs调用一个连续结果的WQS模型,该函数返回一个gwqs类的对象;三个函数gwqs_barplot、gwqs_scatterplot和gwqs_fitted_vs_resid允许绘制图中所示的数字 @ref(fig:model1)。
# we save the names of the mixture variables in the variable "PCBs"
PCBs <- names(wqs_data)[1:34]
# we run the model and save the results in the variable "results"
results <- gwqs(yLBX ~ wqs, mix_name = PCBs, data = wqs_data,
q = 10, validation = 0.6, b = 2, b1_pos = TRUE,
b1_constr = FALSE, family = "gaussian", seed = 2016)
# bar plot
gwqs_barplot(results)
# scatter plot y vs wqs
gwqs_scatterplot(results)
# scatter plot residuals vs fitted values
gwqs_fitted_vs_resid(results)这个WQS模型测试了我们的因变量y和根据暴露浓度分层排序(q=10)估计的WQS指数之间的关系;在gwqs公式中,必须包括wqs项,就像数据集中存在一个wqs变量一样。数据被分成40%的数据集用于训练,60%的数据集用于验证(验证=0.6),并指定2个bootstrap样本(b=2)用于参数估计(在实际应用中我们建议至少使用100个bootstrap样本)。由于WQS提供了对混合效应的单向评价,我们首先检查了从bootstrap模型中得出的权重,其中β1为正(b1_pos = TRUE);我们可以通过设置该参数为假(b1_pos = FALSE)来测试负相关。我们也可以选择在估计权重时将β1约束为正值(b1_pos = TRUE和b1_constr = TRUE)或负值(b1_pos = FALSE和b1_constr = TRUE);在例子1的情况下,我们没有对β1施加约束。我们将我们的模型与高斯分布联系起来,以测试连续结果和暴露之间的关系(family="高斯"),并将种子固定为2016,以获得可重复的结果(种子=2016)。
图@ref(fig:model1) A是一个柱状图,显示了分配给每个变量的权重,从最高权重到最低权重排序。这些结果表明,变量LBXF07LA、LBXD02LA和LBX138LA是这种混合效应的最大贡献者。红色虚线代表截止值ττ(默认情况下等于混合物中元素数量的倒数,如Carrico等人2014年建议的那样),用于区分哪个元素的权重大于零。
在图@ref(fig:model1)的图B中,我们有一个wqs指数与结果的表示(当协变量包含在模型中时,根据模型残差进行调整),显示了暴露和结果之间关联的方向和形状。例如,在这种情况下,我们可以观察到混合物和yLBX变量之间的线性和正向关系。
在图C中,显示了残差与拟合值的诊断图,以检查残差是否在零附近随机分布,或者是否存在趋势。所有这些图都是用ggplot2软件包建立的。
为了测试模型中变量之间关联的统计学意义,必须像经典的R回归函数那样运行以下代码。
summary(results)##
## Call:
## gwqs(formula = yLBX ~ wqs, data = wqs_data, mix_name = PCBs,
## b = 2, b1_pos = TRUE, b1_constr = FALSE, q = 10, validation = 0.6,
## family = "gaussian", seed = 2016)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.9642 -0.6802 -0.0257 0.6717 3.4734
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -4.49333 0.31386 -14.32 <2e-16 ***
## wqs 1.01991 0.06753 15.10 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for gaussian family taken to be 1.210009)
##
## Null deviance: 636.62 on 299 degrees of freedom
## Residual deviance: 360.58 on 298 degrees of freedom
## AIC: 912.54
##
## Number of Fisher Scoring iterations: 2这个结果告诉我们,关联是正的,而且有统计学意义(P<2e-16)。
为了得到估计权重的准确值,我们可以应用results$final_weights命令。下面的代码显示了前六个最高权重;完整的权重列表可以通过省略head函数来调用。
head(results$final_weights)## mix_name mean_weight
## LBX138LA LBX138LA 0.16536064
## LBXF07LA LBXF07LA 0.16257973
## LBXD02LA LBXD02LA 0.13392939
## LBX105LA LBX105LA 0.09774876
## LBXF06LA LBXF06LA 0.05016536
## LBX118LA LBX118LA 0.04785201这些相同的表格也分别通过函数gwqs_summary_tab和gwqs_weights_tab显示在Viewer窗口。这两个函数都使用包kableExtra来产生输出。输出(表@ref(tab:sum1)和@ref(tab:w1))和各自的代码如下所示。
gwqs_summary_tab(results)| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | -4.49 | 0.3140 | -14.3 | 0 |
| wqs | 1.02 | 0.0675 | 15.1 | 0 |
mf_df <- as.data.frame(signif(coef(summary(results$fit)), 3))
kable_styling(kable(mf_df, row.names = TRUE))gwqs_weights_tab(results)| mix_name | mean_weight |
|---|---|
| LBX138LA | 1.65e-01 |
| LBXF07LA | 1.63e-01 |
| LBXD02LA | 1.34e-01 |
| LBX105LA | 9.77e-02 |
| LBXF06LA | 5.02e-02 |
| LBX118LA | 4.79e-02 |
| LBX153LA | 4.21e-02 |
| LBX180LA | 3.81e-02 |
| LBX157LA | 3.80e-02 |
| LBXF05LA | 3.78e-02 |
| LBXD01LA | 3.05e-02 |
| LBX167LA | 2.75e-02 |
| LBX194LA | 2.48e-02 |
| LBXF03LA | 1.91e-02 |
| LBXF08LA | 1.58e-02 |
| LBX099LA | 1.46e-02 |
| LBX156LA | 1.36e-02 |
| LBX187LA | 1.14e-02 |
| LBX170LA | 1.05e-02 |
| LBX199LA | 5.97e-03 |
| LBXF02LA | 5.40e-03 |
| LBX189LA | 5.28e-03 |
| LBXPCBLA | 1.46e-03 |
| LBX074LA | 2.83e-04 |
| LBXTCDLA | 1.84e-05 |
| LBXF09LA | 0.00e+00 |
| LBXD03LA | 0.00e+00 |
| LBXHXCLA | 0.00e+00 |
| LBXD05LA | 0.00e+00 |
| LBXD07LA | 0.00e+00 |
| LBXF04LA | 0.00e+00 |
| LBXF01LA | 0.00e+00 |
| LBXD04LA | 0.00e+00 |
| LBX196LA | 0.00e+00 |
final_weight <- results$final_weights
final_weight[, -1] <- signif(final_weight[, -1], 3)
kable_styling(kable(final_weight, row.names = FALSE))gwqs函数还给出了其他的输出,比如表示求解器是否收敛(0)的值向量(results$conv),包含所有估计权重和相关β1、标准误差、统计数据和每个引导样本的p值的矩阵(results$bres),估计wqs指数的向量(results$wqs),包含用于确定混合物中每个变量的量值的截止点的向量列表(results$qi)。包含每个bootstrap数据集中的受试者行的向量列表(results$bindex),识别每个bootstrap中用于估计权重的受试者行(results$tindex),识别用于估计最终模型参数的受试者行(results$vindex),在每个bootstrap步骤中获得的optima参数估计值的目标函数向量(results$objfn_values)以及来自optim函数的任何消息(results$optim_messages)。
下面的脚本可以重现使用plots函数自动生成的数字。
# bar plot
w_ord <- order(results$final_weights$mean_weight)
mean_weight <- results$final_weights$mean_weight[w_ord]
mix_name <- factor(results$final_weights$mix_name[w_ord],
levels = results$final_weights$mix_name[w_ord])
data_plot <- data.frame(mean_weight, mix_name)
ggplot(data_plot, aes(x = mix_name, y = mean_weight)) +
geom_bar(stat = "identity", color = "black") + theme_bw() +
theme(axis.ticks = element_blank(),
axis.title = element_blank(),
axis.text.x = element_text(color='black'),
legend.position = "none") + coord_flip() +
geom_hline(yintercept = 1/length(PCBs), linetype="dashed", color = "red")
#
# scatter plot y vs wqs
ggplot(results$y_wqs_df, aes(wqs, y_adj)) + geom_point() +
stat_smooth(method = "loess", se = FALSE, size = 1.5) + theme_bw()
#
# scatter plot residuals vs fitted values
fit_df <- data.frame(fitted = fitted(results),
resid = residuals(results, type = "response"))
ggplot(fit_df, aes(x = fitted, y = resid)) + geom_point() +
theme_bw() + xlab("Fitted values") + ylab("Residuals")References
Carrico C, Gennings C, Wheeler D, Factor-Litvak P. Characterization of a weighted quantile sum regression for highly correlated data in a risk analysis setting. J Agricul Biol Environ Stat. 2014:1-21. ISSN: 1085-7117. DOI: 10.1007/ s13253-014-0180-3. http://dx.doi.org/10.1007/s13253-014-0180-3.
Czarnota J, Gennings C, Colt JS, De Roos AJ, Cerhan JR, Severson RK, Hartge P, Ward MH, Wheeler D. 2015. Analysis of environmental chemical mixtures and non-Hodgkin lymphoma risk in the NCI-SEER NHL study. Environmental Health Perspectives.
Czarnota J, Gennings C, Wheeler D. 2015. Assessment of weighted quantile sum regression for modeling chemical mixtures and cancer risk. Cancer Informatics, 2015:14(S2) 159-171.
Curtin P, Kellogg J, Cech N, and Gennings C. A random subset implementation of weighted quantile sum (wqsrs) regression for analysis of high-dimensional mixtures. Communications in Statistics - Simulation and Computation, 0(0):1–16, 2019. doi: 10.1080/03610918.2019.1577971.
Tanner EM, Bornehag CG, and Gennings C. Repeated holdout validation for weighted quantile sum regression. MethodsX, 6:2855 – 2860, 2019. doi: https://doi.org/10.1016/j.mex.2019.11.008.