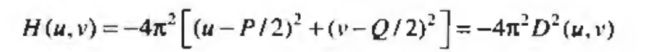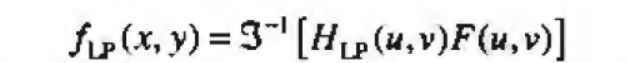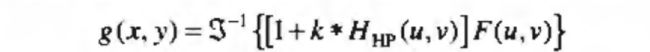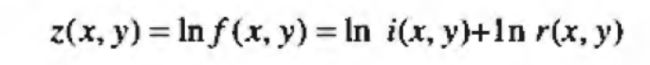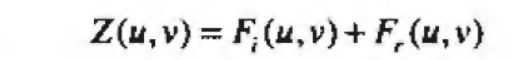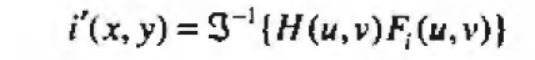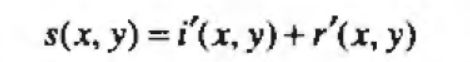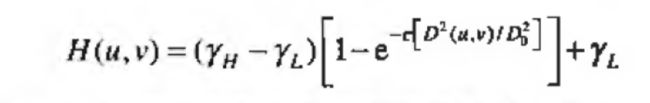opencv图像分析与处理（8）- 使用频率域滤波器进行图像的平滑与锐化【常见的低通/高通滤波器及其C++实现】
本节为opencv数字图像处理（8）：频率域滤波的第五小节，使用频率域滤波器进行图像的平滑与锐化，主要包括：理想低通/高通滤波器，巴特沃斯低通/高通滤波器、高斯低通/高通滤波器、频率域拉普拉斯算子、高频强调滤波器以及同态滤波的介绍和C++实现。
1. 使用低通滤波器进行图像平滑
考虑图像中的边缘与其他尖锐的灰度转变对其傅里叶变换的高频内容有贡献，因此在频率域平滑图像可通过高频分量的衰减来达到，即低通滤波器。比较典型的低通滤波器即理想低通滤波器、布特沃斯低通滤波器和高斯滤波器，对图像的平滑/模糊程度也是由高到底。其中布特沃斯滤波器有一个参数，成为滤波器的阶数，阶数值越高，越接近理想滤波器，反之更像高斯滤波器。
1.1. 理想低通滤波器
在以原点为圆心，以 D 0 D_0 D0为半径的圆内，无衰减地通过所有频率而在该圆外切断所有频率的二维低通滤波器，成为理想低通滤波器（ILPF），它由下面的函数来确定：
其中 D 0 D_0 D0是一个正常数， D ( u , v ) D(u,v) D(u,v)是频率域中点 ( u , v ) (u,v) (u,v)与频率矩形中心的距离，即：
如下图所示，从左到右分别是一个理想低通滤波器变换函数的透视图、以图像形式显示的滤波器和滤波器径向横截面。
使用一个理想低通滤波器进行图像平滑结果与C++代码如下：
C++代码核心部分如下，将代码插入文章底部的框架代码中指定位置即可：
//1.理想低通滤波
cv::Mat idealBlur(padded.size(), CV_32FC2);
double D0 = 60;
for (int i = 0; i < padded.rows; i++) {
float* p = idealBlur.ptr<float>(i);
for (int j = 0; j < padded.cols; j++) {
double d = sqrt(pow((i - padded.rows / 2), 2) + pow((j - padded.cols / 2), 2));//分子,计算pow必须为float型
if (d <= D0) {
p[2 * j + 1] = 1;
p[2 * j] = 1;
}
else {
p[2 * j] = 0;
p[2 * j + 1] = 0;
}
}
}
multiply(complexImg, idealBlur, idealBlur);
cv::idft(idealBlur, idealBlur);
cv::split(idealBlur, plane);
1.2. 巴特沃斯低通滤波器
截止频率位于距原点 D 0 D_0 D0处的 n n n阶巴特沃斯低通滤波器BLPF的传递函数的定义为：
下图显示了BLPF函数的透视图、图像显示和径向剖面图：
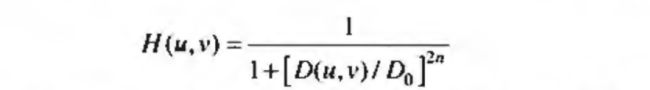
BLPF传递函数并没有在通过频率和滤除频率之间给出明显截止的尖锐的不连续性，使用巴特沃斯低通滤波器的效果与C++代码如下：
C++代码核心部分如下，将代码插入文章底部的框架代码中指定位置即可：
//2.巴特沃斯低通滤波
cv::Mat butterworthBlur(padded.size(), CV_32FC2);
double D0 = 60;
int n = 1;
for (int i = 0; i < padded.rows; i++) {
float* p = butterworthBlur.ptr<float>(i);
for (int j = 0; j < padded.cols; j++) {
double d = sqrt(pow((i - padded.rows / 2), 2) + pow((j - padded.cols / 2), 2));//分子,计算pow必须为float型
p[2*j] = 1.0 / (1 + pow(d / D0, 2 * n));
p[2*j+1] = 1.0 / (1 + pow(d / D0, 2 * n));
}
}
multiply(complexImg, butterworthBlur, butterworthBlur);
cv::idft(butterworthBlur, butterworthBlur);
cv::split(butterworthBlur, plane);
BLPF用于平滑处理，如图像由于量化不足产生伪轮廓时，常可用低通滤波进行平滑以改进图像质量。通常，BLPF的平滑效果好于ILPF，当n的阶数较低时（n=1,2）,没有振铃现象，当阶数较高时会产生明显的振铃现象。
1.3. 高斯低通滤波器
高斯低通滤波器的传递函数如下所示：
其中 D 0 D_0 D0是截止频率，当 D ( u , v ) = D 0 D(u,v)=D_0 D(u,v)=D0时，GLPF下降到其最大值0.607处。GLPF的傅里叶反变换也是高斯的，这意味这空间高斯滤波器将没有振铃。下图从左到右依次是GLPF函数的透视图、图像显示和径向剖面图。
使用高斯低通滤波器平滑图像效果如下：
C++代码核心部分如下，将代码插入文章底部的框架代码中指定位置即可：
//3.高斯低通滤波
cv::Mat gaussianBlur(padded.size(), CV_32FC2);
float D0 = 2 * 1000 ;
for (int i = 0; i < padded.rows; i++)
{
float* p = gaussianBlur.ptr<float>(i);
for (int j = 0; j < padded.cols; j++)
{
float d = pow(i - padded.rows / 2, 2) + pow(j - padded.cols / 2, 2);
p[2 * j] = expf(-d / D0);
p[2 * j + 1] = expf(-d / D0);
}
}
multiply(complexImg, gaussianBlur, gaussianBlur);
cv::idft(gaussianBlur, gaussianBlur);
cv::split(gaussianBlur, plane);
2. 使用高通滤波器进行图像锐化
因为图像的边缘和其他灰度的急剧变化与高频分量有关，所以图像锐化可以通过高通滤波来实现，高通滤波会衰减傅立叶变换中的低频分量而不会扰乱高频信息，一个高通滤波器是从给定的低通滤波器用下式得到：
2.1. 理想高通滤波器
一个二维理想高通滤波器IHPF定义为：
下图从左到右依次表示典型理想高通滤波器的透视图、图像表示和剖面图：
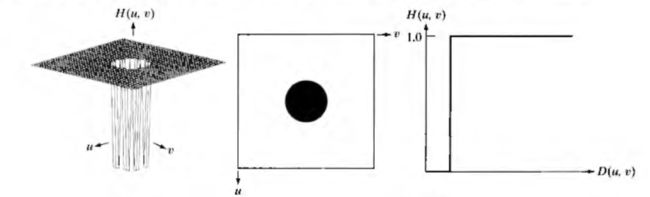
下图显示的是典型理想高通滤波器的空间表示及通过滤波器中心的对应灰度剖面图：
效果和代码如下：
C++代码核心部分如下，将代码插入文章底部的框架代码中指定位置即可：
//4.理想高通滤波
cv::Mat idealBlur(padded.size(), CV_32FC2);
double D0 = 20;
for (int i = 0; i < padded.rows; i++) {
float* p = idealBlur.ptr<float>(i);
for (int j = 0; j < padded.cols; j++) {
double d = sqrt(pow((i - padded.rows / 2), 2) + pow((j - padded.cols / 2), 2));//分子,计算pow必须为float型
if (d <= D0) {
p[2 * j + 1] = 0;
p[2 * j] = 0;
}
else {
p[2 * j] = 1;
p[2 * j + 1] = 1;
}
}
}
multiply(complexImg, idealBlur, idealBlur);
cv::idft(idealBlur, idealBlur);
cv::split(idealBlur, plane);
2.2. 巴特沃斯高通滤波器
截止频率为 D 0 D_0 D0的 n n n阶巴特沃斯高通滤波器BHPF定义为：
下图从左到右依次表示典型理想高通滤波器的透视图、图像表示和剖面图：
下图显示的是典型理想高通滤波器的空间表示及通过滤波器中心的对应灰度剖面图：
效果和C++代码如下：
C++代码核心部分如下，将代码插入文章底部的框架代码中指定位置即可：
//5.巴特沃斯高通滤波
cv::Mat butterworthBlur(padded.size(), CV_32FC2);
double D0 = 20;
int n = 1;
for (int i = 0; i < padded.rows; i++) {
float* p = butterworthBlur.ptr<float>(i);
for (int j = 0; j < padded.cols; j++) {
double d = sqrt(pow((i - padded.rows / 2), 2) + pow((j - padded.cols / 2), 2));//分子,计算pow必须为float型
p[2*j] = 1.0 / (1 + pow(D0 / d, 2 * n));
p[2*j+1] = 1.0 / (1 + pow(D0 / d, 2 * n));
}
}
multiply(complexImg, butterworthBlur, butterworthBlur);
cv::idft(butterworthBlur, butterworthBlur);
cv::split(butterworthBlur, plane);
2.3. 高斯高通滤波器
截止频率处在距频率矩形中心距离为 D 0 D_0 D0的高斯高通滤波器GHPF的传递函数如下：
下图从左到右依次表示典型理想高通滤波器的透视图、图像表示和剖面图：
下图显示的是典型理想高通滤波器的空间表示及通过滤波器中心的对应灰度剖面图：
效果和代码如下所示：
C++代码核心部分如下，将代码插入文章底部的框架代码中指定位置即可：
//6.高斯高通滤波
cv::Mat gaussianBlur(padded.size(), CV_32FC2);
float D0 = 2 * 10 * 10;
for (int i = 0; i < padded.rows; i++)
{
float* p = gaussianBlur.ptr<float>(i);
for (int j = 0; j < padded.cols; j++)
{
float d = pow(i - padded.rows / 2, 2) + pow(j - padded.cols / 2, 2);
p[2 * j] = 1 - expf(-d / D0);
p[2 * j + 1] = 1 - expf(-d / D0);
}
}
multiply(complexImg, gaussianBlur, gaussianBlur);
cv::idft(gaussianBlur, gaussianBlur);
cv::split(gaussianBlur, plane);
2.4. 频率域的拉普拉斯算子
拉普拉斯算子使用如下滤波器在频率与实现：
或者说关于频率矩形的中心，使用如下滤波器：
然后拉普拉斯图像由下式得到：
增强的话可用下式实现：
这里因为 H ( u , v ) H(u,v) H(u,v)是负的，所以 c = − 1 c=-1 c=−1。频率域中上式可汇总为下面的式子：
效果图与C++实现如下：
C++代码核心部分如下，将代码插入文章底部的框架代码中指定位置即可：
//7.频率域拉普拉斯算子
cv::Mat Laplace(padded.size(), CV_32FC2);
for (int i = 0; i < padded.rows; i++)
{
float* p = Laplace.ptr<float>(i);
for (int j = 0; j < padded.cols; j++)
{
float d = pow(i - padded.rows / 2, 2) + pow(j - padded.cols / 2, 2);
p[2 * j] = 1 + 4 * pow(CV_PI, 2) * d;
p[2 * j + 1] = 1 + 4 * pow(CV_PI, 2) * d;
}
}
multiply(complexImg, Laplace, Laplace);
cv::idft(Laplace, Laplace);
cv::split(Laplace, plane);
2.5. 钝化模板、高提升滤波和高频强调滤波
钝化模板技术在频率域：
高提升滤波在频率域：
其中 H L P ( u , v ) H_{LP}(u,v) HLP(u,v)是一个低通滤波器， F ( u , v ) F(u,v) F(u,v)是 f ( x , y ) f(x,y) f(x,y)的傅里叶变换， f L P ( x , y ) f_{LP}(x,y) fLP(x,y)是平滑后的图像。然后，根据下式：
该表达式定义了 k = 1 k=1 k=1时的钝化模板和 k > 1 k>1 k>1时的高提升滤波器。我们可以用涉及低通滤波器的频率域计算来表达上式：
对应地，高通：
其中，方括号中的表达式称为高频强调滤波器。之前提到高通滤波器将直流项设为0，但是高频强调滤波不存在这一问题，更一般地，高频强调滤波的公式如下：
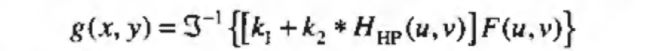
k 1 ≥ 0 k_1\geq 0 k1≥0给出了控制距原点的偏移量， k 2 ≥ 0 k_2\geq 0 k2≥0控制高频的贡献。
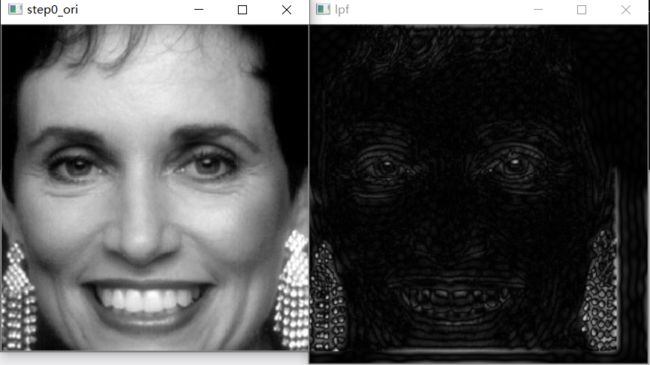
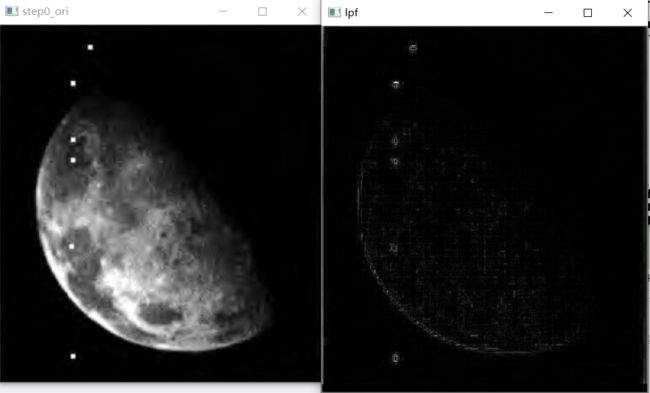
书中给出了一个例子，从左上到右下，图中分别表示原图、高斯高通滤波器、基于高斯滤波的高频强调滤波器以及直方图均衡化后的结果。高频强调滤波
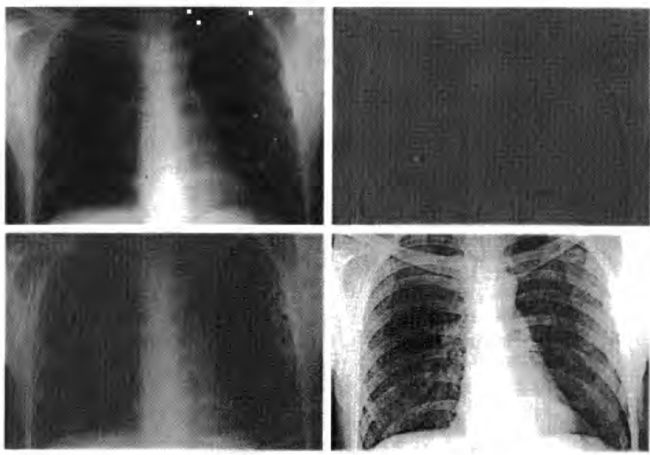
代码比较简单，结合上面的高斯高通滤波实现，比较简单不再重复， 上面的例子取 k 1 = 0.5 ， k 2 = 0.75 k_1=0.5，k_2=0.75 k1=0.5，k2=0.75，有效的保留了灰度缓慢变化的区域。
2.6. 同态滤波
照射-反射模型可用于开发一种频率域处理过程，该过程同时压缩灰度范围和增强对比度来改善一幅图像的表观，一幅图像可表示为其照射分量和反射分量的乘积：
但是傅里叶变换的乘积并不等于乘积的傅立叶变换，即：
但是我们可以定义：
则有：
即：
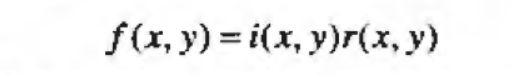
使用一个滤波器对 Z ( u , v ) Z(u,v) Z(u,v)进行滤波：
空间域滤波后的图像：
根据定义有：
和
所以，滤波后空间域的图像可以写为：
最后，因为 z ( x , y ) z(x,y) z(x,y)是通过取输入图像的自然对数形成的，可通过滤波后取指数来形成输出图像：
步骤总结如下：
该方法是以同态系统的一类系统的特殊情况为基础，方法的关键在于照射分量和反射分量的分离。图像的照射分量通常由慢的空间变化来表征，而反射分量往往引起突变，特别是在不同物体的连接部分。这样的特性导致图像取对数后的傅立叶变换的低频分量与照射相联系，而高频成分与反射相联系，虽然只是不强的联系。
同态滤波函数如下：
其中如果 γ L ≤ 1 且 γ H ≥ 1 \gamma_L\leq1且\gamma_H\geq1 γL≤1且γH≥1那么如下图所示的滤波器趋向于衰减低频/照射分量的贡献，而增强高频/反射分量的贡献，常数 c c c控制函数坡度的锐利度，在 γ L 和 γ H \gamma_L和\gamma_H γL和γH之间过渡，类似于高频强调滤波：
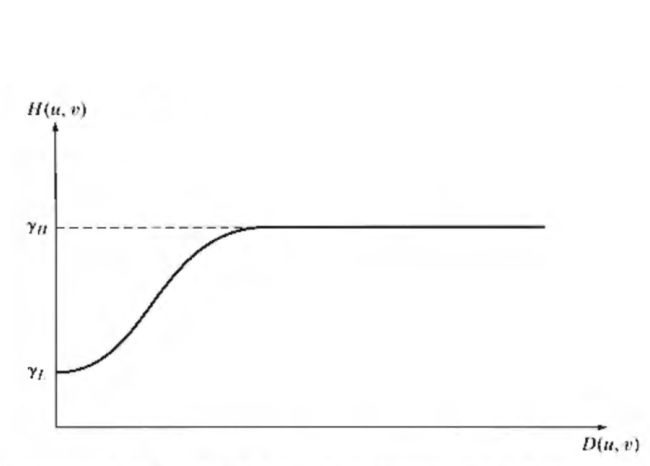
该滤波器实现起来也比较简单，不再重复。书中给出了一个同台滤波的例子如下所示，其中 γ L = 0.25 , γ H = 2 , c = 1 , D 0 = 80 \gamma_L=0.25,\gamma_H=2,c=1,D_0=80 γL=0.25,γH=2,c=1,D0=80：
文中提到的代码框架：
#if 1
#include "opencv2/opencv.hpp"
int main()
{
cv::Mat input = cv::imread("2.JPG", cv::IMREAD_GRAYSCALE);
cv::imshow("step0_ori", input);
int w = cv::getOptimalDFTSize(input.cols);
int h = cv::getOptimalDFTSize(input.rows);
cv::Mat padded;
cv::copyMakeBorder(input, padded, 0, h - input.rows, 0, w - input.cols,
cv::BORDER_CONSTANT, cv::Scalar::all(0));
padded.convertTo(padded, CV_32FC1);
cv::imshow("step1_padded", padded);
for (int i = 0; i < padded.rows; i++)
{
float* ptr = padded.ptr<float>(i);
for (int j = 0; j < padded.cols; j++)
ptr[j] *= pow(-1, i + j);
}
cv::imshow("step2_center", padded);
cv::Mat plane[] = { padded,cv::Mat::zeros(padded.size(),CV_32F) };
cv::Mat complexImg;
cv::merge(plane, 2, complexImg);
cv::dft(complexImg, complexImg);
cv::split(complexImg, plane);
cv::magnitude(plane[0], plane[1], plane[0]);
plane[0] += cv::Scalar::all(1);
cv::log(plane[0], plane[0]);
cv::normalize(plane[0], plane[0], 1, 0, cv::NORM_MINMAX);
cv::imshow("dft", plane[0]);
/***************************************************************************/
//插入
/***************************************************************************/
cv::magnitude(plane[0], plane[1], plane[0]);
cv::normalize(plane[0], plane[0], 1, 0, cv::NORM_MINMAX);
cv::imshow("lpf", plane[0]);
cv::waitKey();
return 0;
}
#endif
欢迎扫描二维码关注微信公众号 深度学习与数学 [每天获取免费的大数据、AI等相关的学习资源、经典和最新的深度学习相关的论文研读，算法和其他互联网技能的学习，概率论、线性代数等高等数学知识的回顾]
