opencv-张氏标定法(前篇)

现在做的很多东西第一步都离不开相机的标定，就将著名的大牛张友正的张氏标定法开始吧！
原文如下：《A Flexible New Technique for Camera Calibration》直接谷歌学术可以很快速的找到原文
第一次，直接看，肯定是不太好看懂的，特别是像我这种没学过计算机图形学的人，相当于就把自己的一个
学习过程记录一下了。

列一下主要参考的博客，(如有不明白相信以下博客会给你解决的)

齐次坐标：http://blog.csdn.net/u011460215/article/details/40696679

单应性矩阵的理解：http://blog.csdn.net/zinnc/article/details/52319491

玉米博主系列（大赞）：http://blog.csdn.net/onthewaysuccess/article/details/40716731

相机模型(内参，外参)：http://blog.csdn.net/u010128736/article/details/52850444

图像几何变换之仿射变换：https://www.cnblogs.com/liekkas0626/p/5238564.html

张正友标定法示例(含源代码)：http://www.cnblogs.com/riddick/p/6696858.html

基于OpenCV立体视觉标定和校正：http://blog.csdn.net/lijiayu2015/article/details/53079661

1.齐次坐标

百度百科有一个简单的介绍（维基应该更好）

齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示，是指一个用于投影几何里的坐标系统，如同用于欧氏几何里的笛卡儿坐标一般。

概括来说：

• 投影平面上的任何点都可以表示成一三元组(X,Y,Z)，称之为该点的’齐次坐标或投影坐标，其中 X、Y 及 Z 不全为 0。
• 以齐次坐标表表示的点，若该坐标内的数值全乘上一相同非零实数，仍会表示该点。
• 相反地，两个齐次坐标表示同一点，当且仅当其中一个齐次坐标可由另一个齐次坐标乘上一相同非零常数得取得。
• 当 Z 不为 0，则该点表示欧氏平面上的该(X/Z,Y/Z)。
• 当 Z 为 0，则该点表示一无穷远点。
• 注意，三元组(0, 0, 0)不表示任何点。原点表示为(0, 0, 1)。

举个简单的例子

齐次坐标[8,4,2]、[4,2,1]表示的都是二维点[4,2]，显然一个向量的齐次表示是不唯一的，齐次坐标的h取不同的值都表示的是同一个点。

齐次坐标表示是计算机图形学的重要手段之一，它既能够用来明确区分向量和点，同时也更易用于进行仿射（线性）几何变换。”——F.S. Hill, JR。
理解齐次坐标http://www.cnblogs.com/csyisong/archive/2008/12/09/1351372.html
这篇博客很好的解释了运用齐次坐标如何区分向量与点的表示方式，解释了上面那句名言的原因，可以跳转一阅，篇幅太长，就不摘录过来了。

2.仿射变换
仿射变换（Affine Transformation 或Affine Map）是一种二维坐标（x, y）到二维坐标（u, v）的线性变换，其数学表达式形式如下：

{u=a1x+b1y+c1y=a2x+b2y+c2(1) (1) { u = a 1 x + b 1 y + c 1 y = a 2 x + b 2 y + c 2

图像处理中，可应用仿射变换对二维图像进行平移、缩放、旋转等操作。以矩阵表达式来计算这些变换时，平移是矩阵相加，旋转和缩放则是矩阵相乘，综合起来可以表示为:
p′=m1∗p+m2 p ′ = m 1 ∗ p + m 2 ( m1 m 1 旋转缩放矩阵， m2 m 2 为平移矩阵， p p 为原向量，p′ p ′ 为变换后的向量)。引入齐次坐标的目的主要是合并矩阵运算中的乘法和加法，表示为 p′=M∗p p ′ = M ∗ p 的形式。即它提供了用矩阵运算把二维、三维甚至高维空间中的一个点集从一个坐标系变换到另一个坐标系的有效方法。它可以表示无穷远的点。n+1维的齐次坐标中如果h=0，实际上就表示了n维空间的一个无穷远点。

上述仿射变换表达式(1)如果用普通坐标来表达会是下面这个样子：

[uv]=[a1a2b1b2][xy]+[c1c2](2) (2) [ u v ] = [ a 1 b 1 a 2 b 2 ] [ x y ] + [ c 1 c 2 ]

对应的齐次坐标矩阵表示形式为：

⎡⎣⎢uv1⎤⎦⎥=⎡⎣⎢a1a20b1b20c1c21⎤⎦⎥⎡⎣⎢xy1⎤⎦⎥(3) (3) [ u v 1 ] = [ a 1 b 1 c 1 a 2 b 2 c 2 0 0 1 ] [ x y 1 ]

下面附录一张二维图像一系列变换对应的齐次矩阵表(具体包括：平移（Translation）、缩放（Scale）、旋转（Rotation）、翻转（Flip）和错切（Shear）)

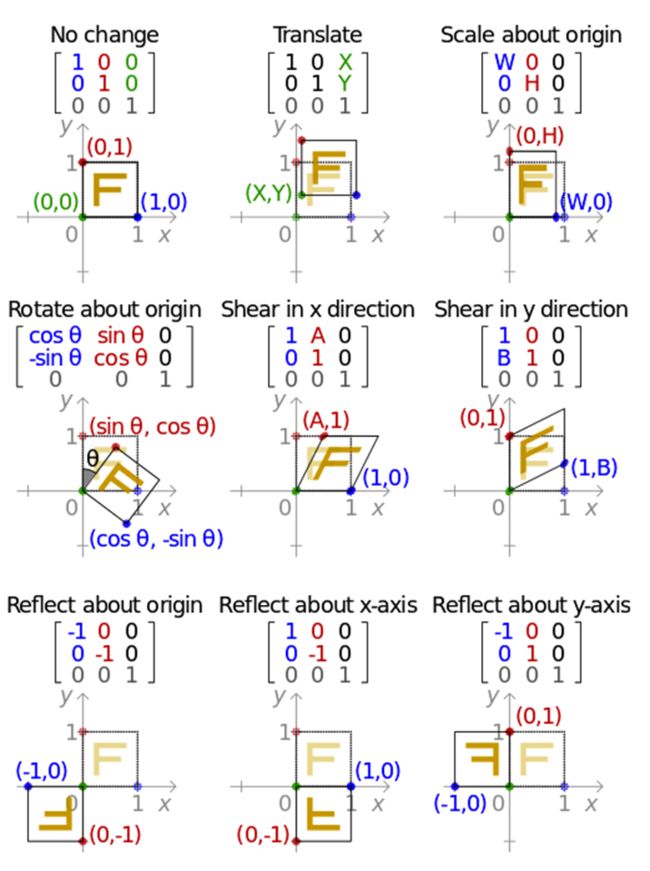
3.三大坐标系

相机标定的两个主要目的：
1建立成像几何模型(建立物体从三维世界到成像平面上各坐标点的对应关系)
2.矫正透镜畸变

实现目的一的铺垫：三大坐标系

先看一个三个坐标的示意简图，通过它大家可以对三个坐标有一个直观的认识，不至于很懵。

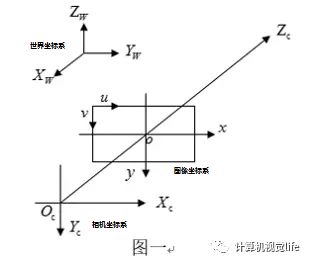
世界坐标系 (XW,YW,ZW) ( X W , Y W , Z W ) ：用户定义的三维世界的坐标系，为了描述目标物在真实世界里的位置而被引入。单位为m。

摄像机坐标系 (XC,YC,ZC) ( X C , Y C , Z C ) ：在相机上建立的坐标系，为了从相机的角度描述物体位置而定义，作为沟通世界坐标系和图像/像素坐标系的中间一环。单位为m。

图像坐标系 (x,y) ( x , y ) :为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系而引入，方便进一步得到像素坐标系下的坐标。 单位为m。、

像素坐标系 (u,v) ( u , v ) :为了描述物体成像后的像点在数字图像上（相片）的坐标而引入，是我们真正从相机内读取到的信息所在的坐标系。单位为个（像素数目）

(备注：)有很多人把图像坐标系和像素坐标系合在一起，称作三大坐标系，也有人分开，称为四大坐标系。

(x,y)坐标系的原点位于摄像机光轴与成像平面的焦点 O′(u0,v0) O ′ ( u 0 , v 0 ) 上，单位为长度单位(米)。 (u,v) ( u , v ) 坐标系的原点在图片的左上角（其实是存储器的首地址）如上图所示，单位为数量单位(个)。 (x,y) ( x , y ) 主要用于表征物体从摄像机坐标系向图像坐标系的透视投影关系。而 (u,v) ( u , v ) 则是实实在在的，我们能从摄像机中得到的真实信息。

棋盘概念：

棋盘是一块由黑白方块间隔组成的标定板，我们用它来作为相机标定的标定物（从真实世界映射到数字图像内的对象）。之所以我们用棋盘作为标定物是因为平面棋盘模式更容易处理（相对于复杂的三维物体），但与此同时，二维物体相对于三维物体会缺少一部分信息，于是我们会多次改变棋盘的方位来捕捉图像，以求获得更丰富的坐标信息。如下图所示，是相机在不同方向下拍摄的同一个棋盘图像。

然后下面是上面一篇博主用手机拍摄的不同角度的九副棋盘图。（我的图片还没有整理好，代码这一部分还有待详细琢磨）

接下来主要梳理几大坐标系的转换，有了这些知识铺垫，后面的理解相信不难。

下面给出了一个简单的图示
图中显示，世界坐标系通过刚体变换到达摄像机坐标系，然后摄像机坐标系通过透视投影变换到达图像坐标系。可以看出，世界坐标与图像坐标的关系建立在刚体变换和透视投影变换的基础上。,.

从世界坐标系-相机坐标系(刚体变换)

刚体变换(regidbody motion):三维空间中，当物体不发生形变时，对一个几何物体作旋转， 平移的运动，称之为刚体变换。
因为世界坐标系和摄像机坐标都是右手坐标系，所以其不会发生形变。我们想把世界坐标系下的坐标转换到摄像机坐标下的坐标，如下图所示，可以通过刚体变换的方式。空间中一个坐标系，总可以通过刚体变换转换到另外一个个坐标系的。

下面看一下，二者之间刚体变换的数学表达。

⎡⎣⎢XCYCZC⎤⎦⎥=⎡⎣⎢r00r10r20r01r11r21r02r12r22⎤⎦⎥⎡⎣⎢XWYWZW⎤⎦⎥+⎡⎣⎢TXTYTZ⎤⎦⎥(1) (1) [ X C Y C Z C ] = [ r 00 r 01 r 02 r 10 r 11 r 12 r 20 r 21 r 22 ] [ X W Y W Z W ] + [ T X T Y T Z ]

对应的齐次表达式为：

⎡⎣⎢⎢⎢XCYCZC1⎤⎦⎥⎥⎥=[R0T3t1]⎡⎣⎢⎢⎢XWYWZW1⎤⎦⎥⎥⎥=[r1r2r3t]⎡⎣⎢⎢⎢XWYW01⎤⎦⎥⎥⎥=[r1r2t]⎡⎣⎢XWYW1⎤⎦⎥(2) (2) [ X C Y C Z C 1 ] = [ R t 0 3 T 1 ] [ X W Y W Z W 1 ] = [ r 1 r 2 r 3 t ] [ X W Y W 0 1 ] = [ r 1 r 2 t ] [ X W Y W 1 ]

其中，R为旋转矩阵，t为平移向量，因为假定在世界坐标系中物点所在平面过世界坐标系原点且与Zw轴垂（也即棋盘平面与 XW−YW X W − Y W 平面重合，目的在于方便后续计算），所以 ZW=0 Z W = 0 ，可直接转换成式(2)的形式。其中变换矩阵:

[R0T3t1](3) (3) [ R t 0 3 T 1 ]

即我们常说的 外参矩阵之所称之为外参矩阵可以理解为只与相机外部参数有关，且外参矩阵随刚体位置的变化而变化。

从相机坐标系-理想图像坐标系
这一过程进行了从三维坐标到二维坐标的转换，也即投影透视过程（用中心投影法将物体投射到投影面上，从而获得的一种较为接近视觉效果的单面投影图，也就是使我们人眼看到景物近大远小的一种成像方式）。我们还是拿针孔成像来说明（除了成像亮度低外，成像效果和透镜成像是一样的，但是光路更简单）

针孔模型
下图是针孔摄像机的基本模型。平面π称为摄像机的像平面，点 Oc O c 称为摄像机中心（或光心），f成为摄像机的焦距， Oc O c 为端点且垂直于像平面的射线成为光轴或主轴，主轴与像平面的交点p是摄像机的主点。

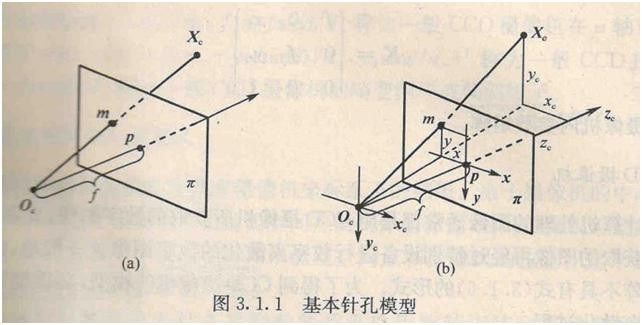
如图所示，图像坐标系为o-xy，摄像机坐标系为 Oc−xcyczc O c − x c y c z c 。记空间点 XC X C 在摄像机坐标系中的齐次坐标为:

XC=(xc,yc,zc,1)T(4) (4) X C = ( x c , y c , z c , 1 ) T

它的像点m在图像坐标系中的齐次坐标记为

m=(x,y,1)T(5) (5) m = ( x , y , 1 ) T

根据三角形相似原理，可得：

{x=fxczcy=fyczc(6) (6) { x = f x c z c y = f y c z c

可以得到:

ZC⎡⎣⎢xy1⎤⎦⎥=⎡⎣⎢f000f0001000⎤⎦⎥⎡⎣⎢⎢⎢xcyczc1⎤⎦⎥⎥⎥=⎡⎣⎢f000f0001⎤⎦⎥⎡⎣⎢100010001000⎤⎦⎥⎡⎣⎢⎢⎢xcyczc1⎤⎦⎥⎥⎥(7) (7) Z C [ x y 1 ] = [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ x c y c z c 1 ] = [ f 0 0 0 f 0 0 0 1 ] [ 1 0 0 0 0 1 0 0 0 0 1 0 ] [ x c y c z c 1 ]

理想图像坐标系到实际图像坐标系(考虑畸变)
透镜的畸变主要分为径向畸变和切向畸变，还有薄透镜畸变等等，但都没有径向和切向畸变影响显著，所以我们在这里只考虑径向和切向畸变。
径向畸变是由于透镜形状的制造工艺导致。且越向透镜边缘移动径向畸变越严重。下图所示是径向畸变的两种类型：桶形畸变和枕形畸变。

它们在真实照片中是这样的：

因为在实际情况下，径向畸变较小，所以其可以用主点(principle point)周围的泰勒级数展开的前几项进行描述。数学表达式如下：

{xrcorr=xp(1+k1r2+k2r4+k3r6)yrcorr=yp(1+k1r2+k2r4+k3r6) { x r c o r r = x p ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) y r c o r r = y p ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 )

由此可知对于径向畸变，我们有3个畸变参数需要求解。

切向畸变是由于透镜和CMOS或者CCD的安装位置误差导致。因此，如果存在切向畸变，一个矩形被投影到成像平面上时，很可能会变成一个梯形。切向畸变需要两个额外的畸变参数来描述，矫正前后的坐标关系为：

{xtcorr=xp+[2p1xpyp+p2(r2+2xp2)]ytcorr=yp+[p1(r2+2yp2)+2p2xpyp] { x t c o r r = x p + [ 2 p 1 x p y p + p 2 ( r 2 + 2 x p 2 ) ] y t c o r r = y p + [ p 1 ( r 2 + 2 y p 2 ) + 2 p 2 x p y p ]

由此可知对于切向畸变，我们有2个畸变参数需要求解。

综上，我们一共需要5个畸变参数（k1、k2、k3、p1和p2 ）来描述透镜畸变。

从实际图像坐标系到像素坐标系
由于定义的像素坐标系原点与图像坐标系原点不重合，假设像素坐标系原点在图像坐标系下的坐标为 （u0，v0） （ u 0 ， v 0 ） ，每个像素点在图像坐标系x轴、y轴方向的尺寸为： dx、dy d x 、 d y ，且像点在实际图像坐标系下的坐标为 （xc，yc） （ x c ， y c ） ，于是可得到像点在像素坐标系下的坐标为：

{u=xcdx+u0v=ycdy+v0(8) (8) { u = x c d x + u 0 v = y c d y + v 0

化为齐次坐标表现形式可以得到:

⎡⎣⎢uv1⎤⎦⎥=⎡⎣⎢⎢1dx0001dy0u0v01⎤⎦⎥⎥⎡⎣⎢xcyc1⎤⎦⎥(9) (9) [ u v 1 ] = [ 1 d x 0 u 0 0 1 d y v 0 0 0 1 ] [ x c y c 1 ]

公式7中 (xc,yc) ( x c , y c ) 与公式9中(x_c, y_c)相同，都是图像坐标系下的坐标。
若暂不考虑透镜畸变，则将式7与式9的转换矩阵相乘即为内参矩阵M：

最后用一幅图来总结从世界坐标系到像素坐标系（不考虑畸变）的转换关系：

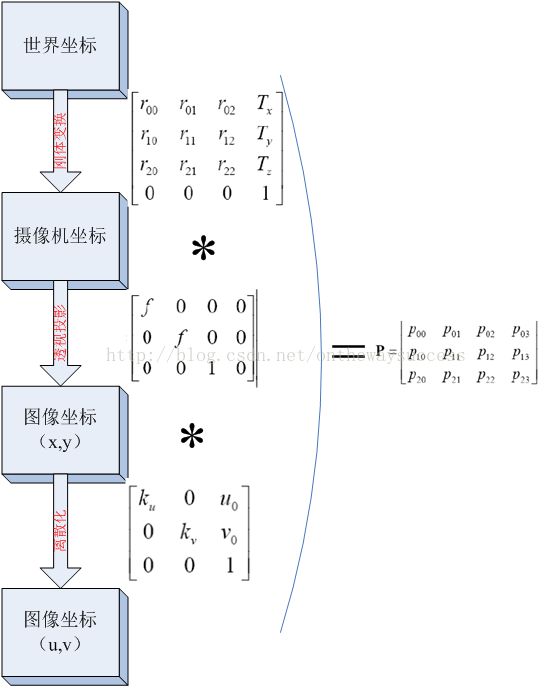
这张图说明几个地方：
首先是P矩阵的一个求解过程：

P=⎡⎣⎢⎢1dx0001dy0u0v01⎤⎦⎥⎥⎡⎣⎢f000f0001000⎤⎦⎥⎡⎣⎢⎢⎢r00r10r200r01r11r210r02r12r220TXTYTZ1⎤⎦⎥⎥⎥ P = [ 1 d x 0 u 0 0 1 d y v 0 0 0 1 ] [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ r 00 r 01 r 02 T X r 10 r 11 r 12 T Y r 20 r 21 r 22 T Z 0 0 0 1 ]

其中图中

{ku=1dxkv=1dy+v0 { k u = 1 d x k v = 1 d y + v 0

我们在进行坐标系转换的时候，转换矩阵一直都是在左乘运算，而矩阵的乘法不满足交换率，所以最后的转换矩阵应该是由上至下不断的左乘得到的。

P就是世界坐标到图像坐标的直接联系人，P就表示了一个投影相机，有下面公式：

W˜=PX˜ W ~ = P X ~

其中:

P=⎡⎣⎢P00P10P20P01P11P21P02P12P22P03P13P23⎤⎦⎥ P = [ P 00 P 01 P 02 P 03 P 10 P 11 P 12 P 13 P 20 P 21 P 22 P 23 ]

好的，下一篇继续！