机器学习＜降维和度量学习＞-matlab代码#3

测试样本：

西瓜数据样本,密度,含糖量：

% 西瓜数据样本
% 密度，含糖量
D=[0.697 0.460;
    0.774 0.376;
    0.634 0.264;
    0.608 0.318;
    0.556 0.215;
    0.403 0.237;
    0.481 0.149;
    0.437 0.211;
    0.666 0.091;
    0.243 0.267;
    0.245 0.057;
    0.343 0.099;
    0.639 0.161;
    0.657 0.198;
    0.360 0.370;
    0.593 0.042;
    0.719 0.103;
    0.359 0.188;
    0.339 0.241;
    0.282 0.257;
    0.748 0.232;
    0.714 0.346;
    0.483 0.312;
    0.478 0.437;
    0.525 0.369;
    0.751 0.489;
    0.532 0.472;
    0.473 0.376;
    0.725 0.445;
    0.446 0.459;];
[m,n]=size(D);
% 归一化
meanD=sum(D)./m;
D=D-meanD;
% 训练标签
y=[zeros(length(1:8),1);
   ones(length(9:21),1);
   zeros(length(22:30),1);];

---

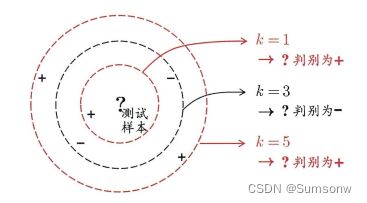
K近邻学习-K-nearest Neighbor

[test_m,test_n]=size(Test_D);

% kNN的参数确定
k=3;
dismatrix=zeros(m,test_m);
for i=1:test_m
    for j=1:m
        dismatrix(j,i)=norm(Test_D(i,:)-D(j,:));
    end
    distemp=dismatrix(:,i);
    %distemp(i,:)=[];
    [~,index]=sort(distemp);
    index_KNN=index(1:k);
    numclass(1,i)=sum(y(index_KNN)==1);
    numclass(2,i)=sum(y(index_KNN)==0);
    if numclass(1,i)>numclass(2,i)
        test_y(i)=1;
    else
        test_y(i)=0;
    end
end
%% 显示
figure(1)
plot(D(y==1,1),D(y==1,2),'bo','MarkerSize',12,'LineWidth',2)
hold on
grid on
plot(D(y==0,1),D(y==0,2),'bx','MarkerSize',12,'LineWidth',2)
plot(Test_D(test_y==1,1),Test_D(test_y==1,2),'ro','MarkerSize',12,'LineWidth',2)
plot(Test_D(test_y==0,1),Test_D(test_y==0,2),'rx','MarkerSize',12,'LineWidth',2)
legend('训练样本-正样本','训练样本-负样本','测试样本-正类','测试样本-负类')
title('KNN算法分类','FontSize',15,'FontWeight',"bold")

---

降维-MDS算法

伪代码

测试数据

N=1000;
%Gaussian noise
noise = 0.001*randn(1,N);
%standard swiss roll data
tt = (3*pi/2)*(1+2*rand(1,N));   height = 21*rand(1,N);
X = [(tt+ noise).*cos(tt); height; (tt+ noise).*sin(tt)];
X=X';
%show the picture
point_size = 20;
figure(1)
cla
scatter3(X(:,1),X(:,2),X(:,3), point_size,tt,'filled');
view([12 12]); grid on; axis on; hold on;
axis on;
axis equal;
hold off;

MDS代码

dim=2;% 降维的维数
testX=X;
[m,n]=size(testX);
D=zeros(m,m);
for i=1:m
    for j=1:m
        D(i,j)=norm(testX(i,:)-testX(j,:),2);
    end
end
e=ones(m,1);
H=eye(m)-1/m*(e*e');
D2=D.*D;
B=-1/2*H'*D2*H;
[eigen_vector,eigen_value]=eig(B);
lambda=diag(eigen_value);
[~,indexe]=sort(lambda,'descend');
lambda=lambda(indexe);
V=eigen_vector(:,indexe);
hat_A=diag(lambda(1:dim));% 选择特定维度的特征值进行降维
hat_V=V(:,1:dim);
Z=hat_V*((hat_A).^(0.5));% 降维特征点数据集
%% 显示降维图像
scatter(Z(:,1),Z(:,2),20,tt,'filled')

---

主成分分析(PCA降维)

伪代码

[m,n]=size(X);
dim=2; % 降维的维度数量dim=3
for j=1:n % 属性值归一化
    X(:,j)=X(:,j)-sum(X(:,j))/m;
end
[W,lambda]=eig(X*X'./(n-1));
lambda=diag(lambda);
[~,index]=sort(-lambda);
lambda=lambda(index);
W=W(:,index);
% 降维的特征值，特征向量
W_dim=W(:,1:dim);
lambda_dim=lambda(1:dim);
%%显示
plot(W_dim(:,1),W_dim(:,2),'b.')
title('PCA主成分分析降维','FontSize',12,'FontWeight',"bold")

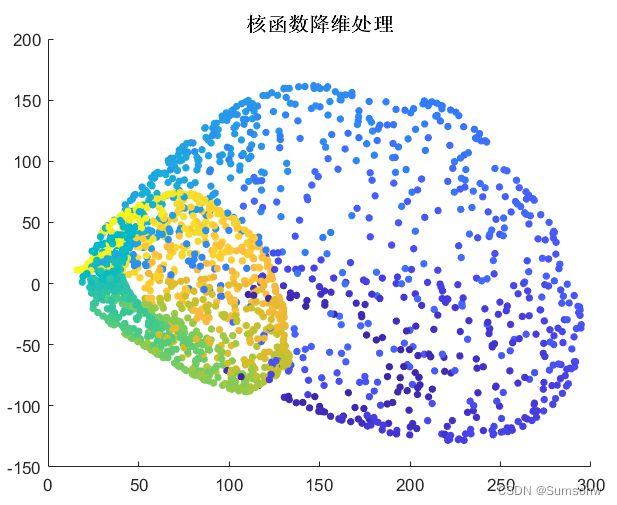
核化线性降维-核化主成分分析（KPCA）

核函数：将低维转换高维

% 降维的维度
dim=2;
% 1.求核函数
M=3;% 选择高斯核函数
Kx=gaussfcn(X,M);
% 2.核函数矩阵的特征分解
[Kx_P,Kx_lambda]=eig(Kx);
Kx_lambda=diag(Kx_lambda);
[~,index]=sort(-Kx_lambda);
Kx_lambda=Kx_lambda(index);
Kx_P=Kx_P(:,index);
% 3.核矩阵降维的特征值，特征向量
newlambda=Kx_lambda(1:dim);
newP=Kx_P(:,1:dim);
% 4.降维的特征向量
W=Kx*Kx'*newP./newlambda';
% 5.降维的数据集
z=(W'*Kx)';
%显示
scatter(z(:,1),z(:,2),20,tt,'filled');
title('核函数降维处理','FontSize',12,'FontWeight',"bold")

流行学习-等度量映射Isometric Mapping

伪代码

% 归一化
[m,n]=size(x);
meanD=sum(x)./m;
x=x-meanD;
% 训练标签
y=[zeros(length(1:8),1);
   ones(length(9:21),1);
   zeros(length(22:30),1);];

% KNN近邻参数设置
Knn=122;
Dismatrix=zeros(m,m);
newDis=inf(m,m);
numclass=zeros(2,m);
for i=1:m
    for j=1:m
        Dismatrix(j,i)=norm(x(i,:)-x(j,:));
    end
    % 确定xi的近邻
    distemp=Dismatrix(:,i);
    [~,index_knn]=sort(distemp);
    index_knn=index_knn(1:Knn);
    newDis(index_knn,i)=distemp(index_knn);
end
%计算最短路径-Floyd算法
a=newDis;
for k=1:m
    for i=1:m
        for j=1:m
            if a(i,j)>a(i,k)+a(k,j)
                a(i,j)=a(i,k)+a(k,j);
            end
        end
    end
end
dis=a;
% MDS降维
dim=2;
e=ones(m,1);
H=eye(m)-1/m*(e*e');
D2=dis.*dis;
B=-1/2*H'*D2*H;
[eigen_vector,eigen_value]=eig(B);
lambda=diag(eigen_value);
[~,indexe]=sort(lambda,'descend');
lambda=lambda(indexe);
V=eigen_vector(:,indexe);
hat_A=diag(lambda(1:dim));% 选择特定维度的特征值进行降维
hat_V=V(:,1:dim);
Z=hat_V*((hat_A).^(0.5));% 降维特征点数据集
%显示
scatter(Z(:,1),Z(:,2),20,tt,'filled')

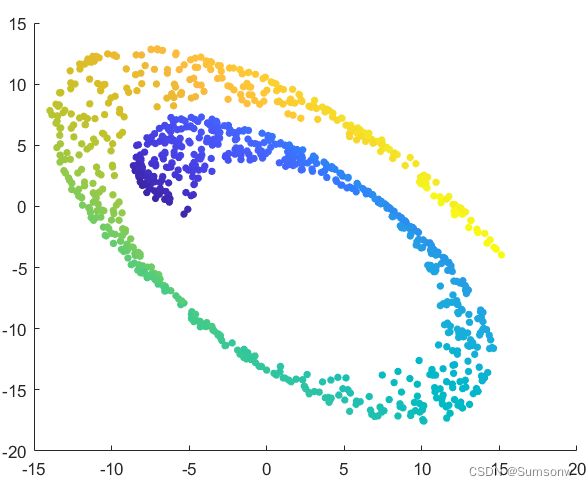
流行学习-LLE算法

伪代码

k=13; %近邻个数
dim=2;% 降维个数
lambda=1e-2; % 运算系数
[m,n]=size(X);
W=zeros(m);
e=ones(k,1);
for i=1:m
    % 求距离
    xx=repmat(X(i,:),m,1);
    diff=xx-X;
    distance_xi=sum(diff.*diff,2);
    % 剔除自身的距离
    [~,pos]=sort(distance_xi);
    index=pos(1:k+1);
    index(index==i)=[];
    % 求权重Wi
    W1=(X(index,:)*X(index,:)')+lambda*eye(k)\e;
    W2=e'*W1;
    W=W1/W2;
    WW(i,index)=W;
end
w_end=sparse(WW);   %w_end就是一个稀疏矩阵
I = eye(m);
A = (I - w_end)' * (I - w_end);
[eigen_vector, eigen_value] = eig(A);
eigen_value=diag(eigen_value);
[~,pos]=sort(eigen_value);
index=pos(1:dim+1); % 采用第2至第d+1个最小特征值对应的特征向量组成新坐标
tran=eigen_vector(:,index);
p=sum(tran.*tran);
j=find(p==min(p));
tran(:, j)=[];
X_LLE=tran;
%显示
scatter(X_LLE(:,1),X_LLE(:,2),20,tt,'filled');
title('LLE算法降维结果','FontSize',12,'FontWeight',"bold")

算法归纳

function Z=myMDS(Test,dim)
    [m,n]=size(Test);
    if dim>n
        error('维度超出属性个数')
    end
    distance=zeros(m,m);
    for i=1:m
        for j=1:m
            distance(i,j)=norm(Test(i,:)-Test(j,:),2);
        end
    end
    e=ones(m,1);
    H=eye(m)-1/m*(e*e');
    B=-1/2*H'*distance.*distance*H;
    [eign_vector,eign_value]=eig(B);
    lambda=diag(eign_value);
    [~,index]=sort(lambda,'descend');
    lambda=lambda(index);
    eign_vector=eign_vector(:,index);
    A=diag(lambda(1:dim));
    V=eign_vector(:,1:dim);
    Z=V*(A.^(1/2));
end
%% PCA函数
function Z=myPCA(test,dim)
    %{
        声明：数据集的每一行，代表一个样本。
    %}
    [m,n]=size(test);
    X=zeros(m,n);
    for j=1:n
        X(:,j)=test(:,j)-sum(test(:,j))/m;
    end
    [W,lambda]=eig(X*X'./(n-1));
    lambda=diag(lambda);
    [~,index]=sort(-lambda);
    lambda=lambda(index);
    W=W(:,index);
    Z=W(:,1:dim);
end
%% 核函数降维
function z=mykerfcn(x,dim,M)
    [m,~]=size(x);
    % 1.求核函数
    %  M : 选择高斯核函数
    if M==1
        % 1.线性核函数
        Kx=x*x';
    elseif M==2
        % 2.多项式核
        Kx=(x*x').^2;
    elseif M==3
        % 3.高斯核
        sigma_k=1.12;
        Kx=zeros(m,m);
        for i=1:m
            for j=1:m
                Kx(i,j)=exp(-norm(x(i,:)-x(j,:))/(2*sigma_k^2));
            end
        end
    elseif M==4
        % 4.拉普拉斯核函数
        Kx=zeros(m,m);
        sigma_Ls=2.75;
        for i=1:m
            for j=1:m
                Kx(i,j)=exp(-norm(x(i,:)-x(j,:),1)/sigma_Ls);
            end
        end
    elseif M==5
        %% 5.sigmoid核函数
        sigmoid_beta=0.3;
        sigmoid_theta=-0.6;
        Kx=zeros(m,m);
        for i=1:m
            for j=1:m
                Kx(i,j)=tanh(sigmoid_beta*x(i,:)*x(j,:)'+sigmoid_theta);
            end
        end
    end
    % 2.核函数矩阵的特征分解
    [Kx_P,Kx_lambda]=eig(Kx);
    Kx_lambda=diag(Kx_lambda);
    [~,index]=sort(-Kx_lambda);
    Kx_lambda=Kx_lambda(index);
    Kx_P=Kx_P(:,index);
    % 3.核矩阵降维的特征值，特征向量
    newlambda=Kx_lambda(1:dim);
    newP=Kx_P(:,1:dim);
    % 4.降维的特征向量
    W=Kx*Kx'*newP./newlambda';
    % 5.降维的数据集
    z=(W'*Kx)';
end

%% LLE算法
function Z=myLLE(X,dim,k,lambda)
    % k 近邻个数
    [m,~]=size(X);
    e=ones(k,1);
    for i=1:m
        % 求距离
        xx=repmat(X(i,:),m,1);
        diff=xx-X;
        distance_xi=sum(diff.*diff,2);
        % 剔除自身的距离
        [~,pos]=sort(distance_xi);
        index=pos(1:k+1);
        index(index==i)=[];
        % 求权重Wi
        W1=(X(index,:)*X(index,:)')+lambda*eye(k)\e;
        W2=e'*W1;
        W=W1/W2;
        WW(i,index)=W;
    end
    w_end=sparse(WW);   %w_end就是一个稀疏矩阵
    I = eye(m);
    A = (I - w_end)' * (I - w_end);
    [eigen_vector, eigen_value] = eig(A);
    eigen_value=diag(eigen_value);
    [~,pos]=sort(eigen_value);
    index=pos(1:dim+1); % 采用第2至第d+1个最小特征值对应的特征向量组成新坐标
    tran=eigen_vector(:,index);
    p=sum(tran.*tran);
    minindex=find(p==min(p));
    tran(:, minindex)=[];
    Z=tran;
end
%% Isomap
function Z=mylsomap(x,dim,Knn)
    [m,~]=size(x);
    Dismatrix=zeros(m,m);
    newDis=inf(m,m);
    for i=1:m
        for j=1:m
            Dismatrix(j,i)=norm(x(i,:)-x(j,:));
        end
        % 确定xi的近邻
        distemp=Dismatrix(:,i);
        [~,index_knn]=sort(distemp);
        index_knn=index_knn(1:Knn);
        newDis(index_knn,i)=distemp(index_knn);
    end
    a=newDis;
    for k=1:m
        for i=1:m
            for j=1:m
                if a(i,j)>a(i,k)+a(k,j)
                    a(i,j)=a(i,k)+a(k,j);
                end
            end
        end
    end
    dis=a;
    e=ones(m,1);
    H=eye(m)-1/m*(e*e');
    D2=dis.*dis;
    B=-1/2*H'*D2*H;
    [eigen_vector,eigen_value]=eig(B);
    lambda=diag(eigen_value);
    [~,indexe]=sort(lambda,'descend');
    lambda=lambda(indexe);
    V=eigen_vector(:,indexe);
    hat_A=diag(lambda(1:dim));% 选择特定维度的特征值进行降维
    hat_V=V(:,1:dim);
    Z=hat_V*((hat_A).^(0.5));% 降维特征点数据集
end