DJL-Java开发者动手学深度学习之使用Softmax进行分类
分类
在之前的文章中,我们介绍了线性回归的基本概念 DJL-Java开发者动手学深度学习之线性回归,并使用高层API实两简单线性回归模型 DJL-Java动手学深度学习之线性回归实现,有预测结果。
回归可以用来预测不少的问题,如我们之前讲的,预测房价、股票、球赛的胜负次数。同时,我们有时遇到的问题并不是预测问题,而是一个分类问题。比如:
- 今天中午午饭吃什么?
- 某个邮件,是否属于垃圾邮件?
- 某个图片,是喵星人还是汪星人?
- 某个人接下来最可能看哪种类型的电影?
- 某个人在特定时间段内,最喜欢购买哪种商品?
通常,机器学习可以通过分类来描述两种微妙差别的问题:
- 我们只对样本类别感兴趣,既哪种类别。
- 我们希望通过对样本类型进行分析,找出每种类别出现的概率。
而往往,这两者的界限很模糊。其中的原因可能是:即使我们只关于分类问题,我们依然要使用分类的概率。
分类问题
我们从一个简单的图片分类问题开始讲起 。假如每次给定一个图片,我们可以用一个标量来表求每一个像素,那么每个图片对应的特征可以表求为 { x 1 , x 2 , x 3 , . . . , x n } \{x_1,x_2,x_3,...,x_n\} {x1,x2,x3,...,xn} 。另外,我们假设每个图片属于喵星人和汪星人的一种。
接下来,我们就可以选择如何用标签进行表求。我们有两个明显的选择:最直接的想法是选择 ( y ∈ { 1 , 2 } ) (y \in \{1, 2\} ) (y∈{1,2}), 其中整数分别代表 { 狗 , 猫 } \{狗, 猫\} {狗,猫}。 这是在计算机上存储此类信息的有效方法。 如果类别间有一些自然顺序, 比如说我们试图预测 { 小 学 , 中 学 , 初 中 , 高 中 , 大 学 } \{小学,中学,初中,高中,大学 \} {小学,中学,初中,高中,大学}, 那么将这个问题转变为回归问题,并且保留这种格式是有意义的。
幸运的是,一般的分类问题并不与类别之间的自然顺序有关。 统计学家很早以前就发明了一种表示分类数据的简单方法:独热编码(one-hot encoding)。 独热编码是一个向量,它的分量和类别一样多。 类别对应的分量设置为1,其他所有分量设置为0。 在我们的例子中,标签 ( y ) (y) (y)将是一个二维向量, 其中 ( 1 , 0 , 0 ) (1, 0, 0) (1,0,0)对应于“猫”、 ( 0 , 1 , 0 ) (0, 1, 0) (0,1,0)对应于“狗”, ( 0 , 0 , 1 ) (0, 0, 1) (0,0,1)对应于“猪”:
y ∈ { ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) , ( 0 , 0 , 1 ) } y \in \{(1, 0, 0), (0, 1, 0),(0, 0, 1)\} y∈{(1,0,0),(0,1,0),(0,0,1)}
网络结构
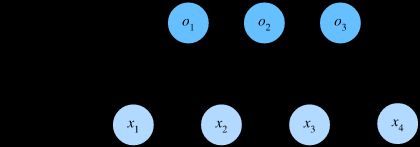
为了估计所有可能类别的条件概率,我们需要一个有多个输出项的模型,每个类别对应一个输出。 为了解决线性模型的分类问题,我们需要和输出一样多的函数。 每个输出对应于一种类型。 在我们的例子中,由于我们有4个特征和3个可能的输出类别, 参考我们之前讲的线程回归,我们可以写出如下预测公式。
f ( x ) = x 1 w 1 + x 2 w 2 + x 3 w 3 + x 4 w 4 + b f(x) = x_1w_1+x_2w_2+x_3w_3+x_4w_4+b f(x)=x1w1+x2w2+x3w3+x4w4+b
我们可以用神经网络图来描述这个计算过程。与线性回归一样,softmax回归也是一个单层神经网络。
为了更简洁地表达模型,我们仍然使用线性代数符号。 通过向量形式表达为 ( y = W x + b ) (\mathbf{y} = \mathbf{W} \mathbf{x} + \mathbf{b}) (y=Wx+b), 这是一种更适合数学和编写代码的形式。 由此,我们已经将所有权重放到一个 ( 3 × 4 ) (3 \times 4) (3×4)矩阵中。 对于给定数据样本的特征 ( x ) (\mathbf{x}) (x), 我们的输出是由权重与输入特征进行矩阵向量乘法再加上偏置 ( b ) (\mathbf{b}) (b)得到的。
损失函数
接下来,我们需要一个损失函数来度量预测的效果。 我们将使用最大似然估计,这与在线性回归 DJL-Java动手学深度学习之线性回归实现 中的方法相同。
假定一个向量 y ^ \hat{\mathbf{y}} y^,我们可以将其视为“任意输入 x ^ \hat{\mathbf{x}} x^的每个类的条件概率”。比如 y ^ 1 = P ( 猫 ∣ x ) \hat{y}_1 =P( 猫 \mid \mathbf{x}) y^1=P(猫∣x)。
我们可以将估计值与实际值进行比较:
P ( Y ∣ X ) = ∏ i = 1 n P ( y ( i ) ∣ x ( i ) ) P(\mathbf{Y} \mid \mathbf{X}) = \prod_{i=1}^n P(\mathbf{y}^{(i)} \mid \mathbf{x}^{(i)}) P(Y∣X)=i=1∏nP(y(i)∣x(i))
根据最大似然估计,我们最大化 ( P ( Y ∣ X ) ) (P(\mathbf{Y} \mid \mathbf{X})) (P(Y∣X)),相当于最小化负对数似然:
− log P ( Y ∣ X ) = ∑ i = 1 n − log P ( y ( i ) ∣ x ( i ) ) = ∑ i = 1 n l ( y ( i ) , y ^ ( i ) ) -\log P(\mathbf{Y} \mid \mathbf{X}) = \sum_{i=1}^n -\log P(\mathbf{y}^{(i)} \mid \mathbf{x}^{(i)}) = \sum_{i=1}^n l(\mathbf{y}^{(i)}, \hat{\mathbf{y}}^{(i)}) −logP(Y∣X)=i=1∑n−logP(y(i)∣x(i))=i=1∑nl(y(i),y^(i))
其中,对于任何标签 ( y ) (\mathbf{y}) (y)和模型预测 ( y ^ ) (\hat{\mathbf{y}}) (y^),损失函数为:
l ( y , y ^ ) = − ∑ j = 1 q y j log y ^ j l(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{j=1}^q y_j \log \hat{y}_j l(y,y^)=−j=1∑qyjlogy^j
通常我们将上面公式称为交叉熵损失(cross-entropy loss)。
模型预测和评估
在训练softmax回归模型后,给出任何样本特征输入,我们可以预测每个输出类别的概率。通常我们使用预测概率最高的类别作为输出类别。
关注公众号,我们后续给出Softmax的代码实现。